Monge beats Bayes: Hardness Results for Adversarial Training

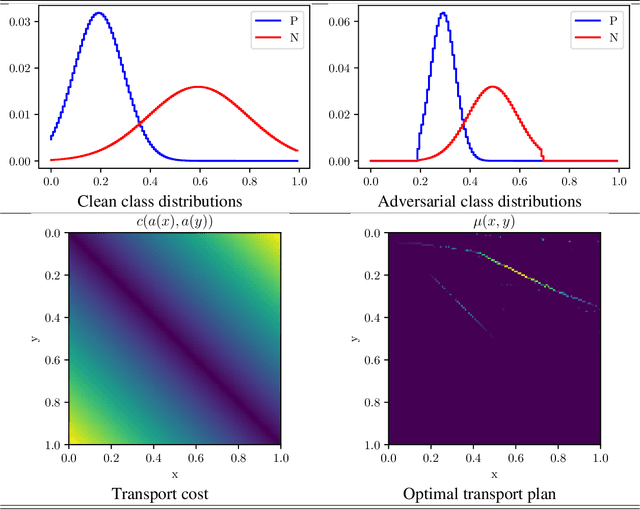
The last few years have seen extensive empirical study of the robustness of neural networks, with a concerning conclusion: several state-of-the-art approaches are highly sensitive to adversarial perturbations of their inputs. There has been an accompanying surge of interest in learning including defense mechanisms against specific adversaries, known as adversarial training. Despite some impressive advances, little remains known on how to best frame a resource-bounded adversary so that it can be severely detrimental to learning, a non-trivial problem which entails at a minimum the choice of loss and classifiers. We suggest here a formal answer to this question, and pin down a simple sufficient property for any given class of adversaries to be detrimental to learning. This property involves a central measure of `harmfulness' which generalizes the well-known class of integral probability metrics. A key feature of our result is that it holds for \textit{all} proper losses, and for a popular subset of these, the optimisation of this central measure appears to be independent of the loss. We show how weakly contractive adversaries for a RKHS can be self-combined to build a maximally detrimental adversary, we show that some implemented existing adversaries involve proxies of our optimal transport adversaries and finally provide a toy experiment assessing such adversaries in a simple context, displaying that additional robustness on testing can be granted through adversarial training.