Generalised Lipschitz Regularisation Equals Distributional Robustness
Paper and Code
Feb 11, 2020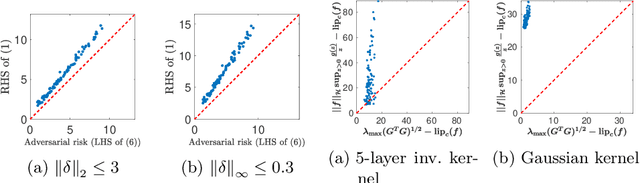
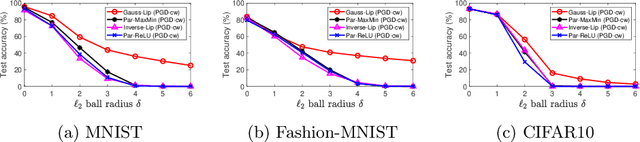
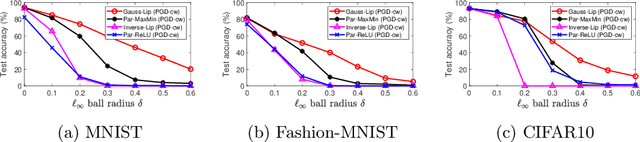
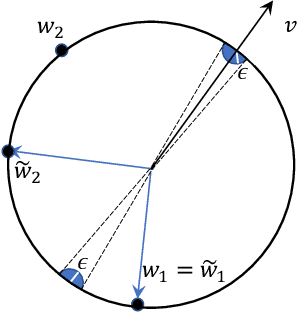
The problem of adversarial examples has highlighted the need for a theory of regularisation that is general enough to apply to exotic function classes, such as universal approximators. In response, we give a very general equality result regarding the relationship between distributional robustness and regularisation, as defined with a transportation cost uncertainty set. The theory allows us to (tightly) certify the robustness properties of a Lipschitz-regularised model with very mild assumptions. As a theoretical application we show a new result explicating the connection between adversarial learning and distributional robustness. We then give new results for how to achieve Lipschitz regularisation of kernel classifiers, which are demonstrated experimentally.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge