Modality Alignment Meets Federated Broadcasting

Federated learning (FL) has emerged as a powerful approach to safeguard data privacy by training models across distributed edge devices without centralizing local data. Despite advancements in homogeneous data scenarios, maintaining performance between the global and local clients in FL over heterogeneous data remains challenging due to data distribution variations that degrade model convergence and increase computational costs. This paper introduces a novel FL framework leveraging modality alignment, where a text encoder resides on the server, and image encoders operate on local devices. Inspired by multi-modal learning paradigms like CLIP, this design aligns cross-client learning by treating server-client communications akin to multi-modal broadcasting. We initialize with a pre-trained model to mitigate overfitting, updating select parameters through low-rank adaptation (LoRA) to meet computational demand and performance efficiency. Local models train independently and communicate updates to the server, which aggregates parameters via a query-based method, facilitating cross-client knowledge sharing and performance improvement under extreme heterogeneity. Extensive experiments on benchmark datasets demonstrate the efficacy in maintaining generalization and robustness, even in highly heterogeneous settings.

FedHPL: Efficient Heterogeneous Federated Learning with Prompt Tuning and Logit Distillation

Federated learning (FL) is a popular privacy-preserving paradigm that enables distributed clients to collaboratively train models with a central server while keeping raw data locally. In practice, distinct model architectures, varying data distributions, and limited resources across local clients inevitably cause model performance degradation and a slowdown in convergence speed. However, existing FL methods can only solve some of the above heterogeneous challenges and have obvious performance limitations. Notably, a unified framework has not yet been explored to overcome these challenges. Accordingly, we propose FedHPL, a parameter-efficient unified $\textbf{Fed}$erated learning framework for $\textbf{H}$eterogeneous settings based on $\textbf{P}$rompt tuning and $\textbf{L}$ogit distillation. Specifically, we employ a local prompt tuning scheme that leverages a few learnable visual prompts to efficiently fine-tune the frozen pre-trained foundation model for downstream tasks, thereby accelerating training and improving model performance under limited local resources and data heterogeneity. Moreover, we design a global logit distillation scheme to handle the model heterogeneity and guide the local training. In detail, we leverage logits to implicitly capture local knowledge and design a weighted knowledge aggregation mechanism to generate global client-specific logits. We provide a theoretical guarantee on the generalization error bound for FedHPL. The experiments on various benchmark datasets under diverse settings of models and data demonstrate that our framework outperforms state-of-the-art FL approaches, with less computation overhead and training rounds.

PPIDSG: A Privacy-Preserving Image Distribution Sharing Scheme with GAN in Federated Learning

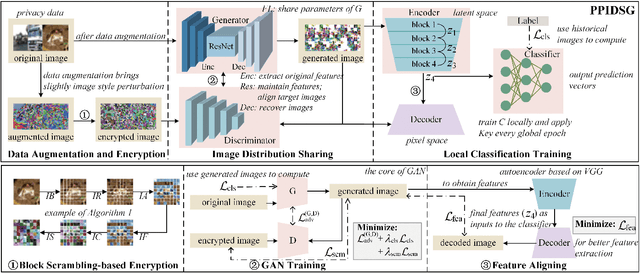
Federated learning (FL) has attracted growing attention since it allows for privacy-preserving collaborative training on decentralized clients without explicitly uploading sensitive data to the central server. However, recent works have revealed that it still has the risk of exposing private data to adversaries. In this paper, we conduct reconstruction attacks and enhance inference attacks on various datasets to better understand that sharing trained classification model parameters to a central server is the main problem of privacy leakage in FL. To tackle this problem, a privacy-preserving image distribution sharing scheme with GAN (PPIDSG) is proposed, which consists of a block scrambling-based encryption algorithm, an image distribution sharing method, and local classification training. Specifically, our method can capture the distribution of a target image domain which is transformed by the block encryption algorithm, and upload generator parameters to avoid classifier sharing with negligible influence on model performance. Furthermore, we apply a feature extractor to motivate model utility and train it separately from the classifier. The extensive experimental results and security analyses demonstrate the superiority of our proposed scheme compared to other state-of-the-art defense methods. The code is available at https://github.com/ytingma/PPIDSG.

Stabilized Sparse Online Learning for Sparse Data

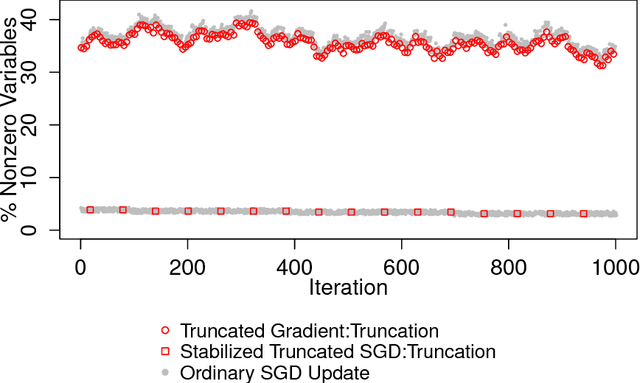
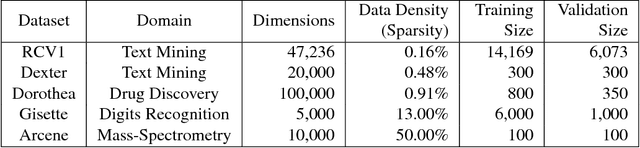
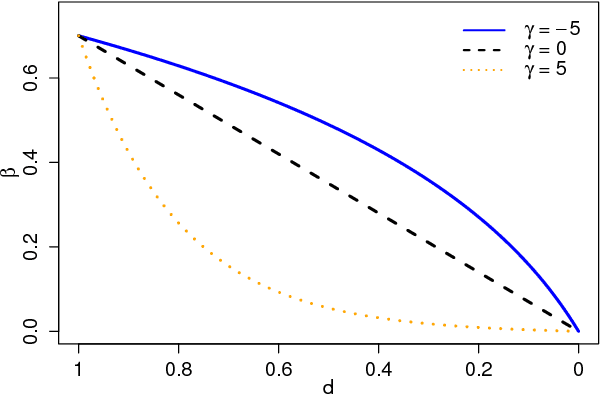
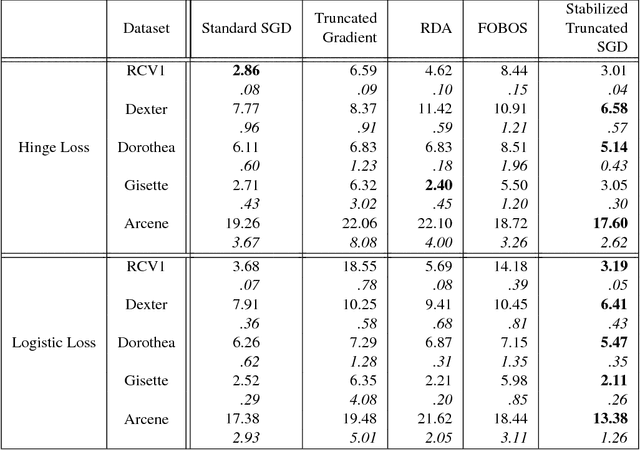
Stochastic gradient descent (SGD) is commonly used for optimization in large-scale machine learning problems. Langford et al. (2009) introduce a sparse online learning method to induce sparsity via truncated gradient. With high-dimensional sparse data, however, the method suffers from slow convergence and high variance due to the heterogeneity in feature sparsity. To mitigate this issue, we introduce a stabilized truncated stochastic gradient descent algorithm. We employ a soft-thresholding scheme on the weight vector where the imposed shrinkage is adaptive to the amount of information available in each feature. The variability in the resulted sparse weight vector is further controlled by stability selection integrated with the informative truncation. To facilitate better convergence, we adopt an annealing strategy on the truncation rate, which leads to a balanced trade-off between exploration and exploitation in learning a sparse weight vector. Numerical experiments show that our algorithm compares favorably with the original algorithm in terms of prediction accuracy, achieved sparsity and stability.

Boosted Sparse Non-linear Distance Metric Learning

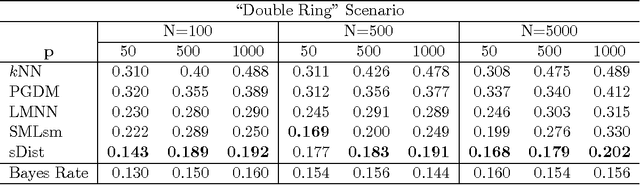
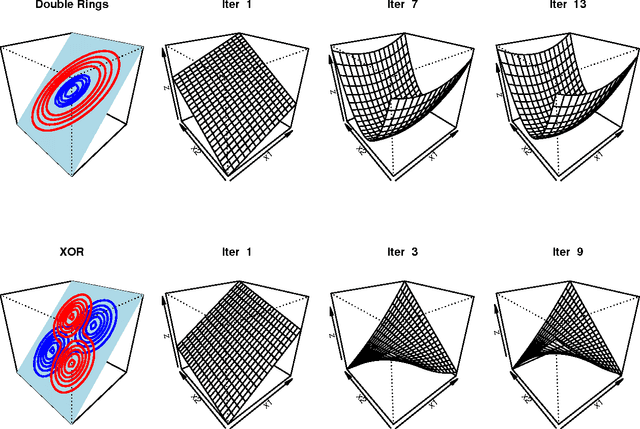
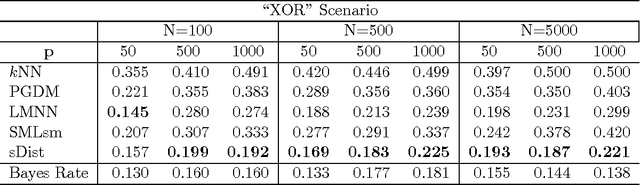
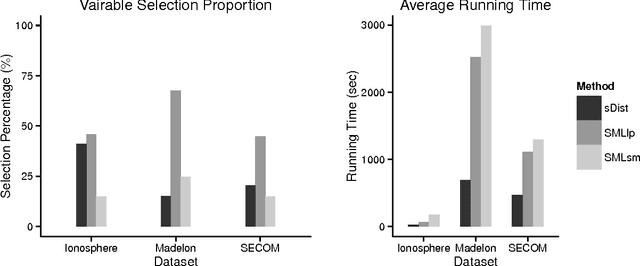
This paper proposes a boosting-based solution addressing metric learning problems for high-dimensional data. Distance measures have been used as natural measures of (dis)similarity and served as the foundation of various learning methods. The efficiency of distance-based learning methods heavily depends on the chosen distance metric. With increasing dimensionality and complexity of data, however, traditional metric learning methods suffer from poor scalability and the limitation due to linearity as the true signals are usually embedded within a low-dimensional nonlinear subspace. In this paper, we propose a nonlinear sparse metric learning algorithm via boosting. We restructure a global optimization problem into a forward stage-wise learning of weak learners based on a rank-one decomposition of the weight matrix in the Mahalanobis distance metric. A gradient boosting algorithm is devised to obtain a sparse rank-one update of the weight matrix at each step. Nonlinear features are learned by a hierarchical expansion of interactions incorporated within the boosting algorithm. Meanwhile, an early stopping rule is imposed to control the overall complexity of the learned metric. As a result, our approach guarantees three desirable properties of the final metric: positive semi-definiteness, low rank and element-wise sparsity. Numerical experiments show that our learning model compares favorably with the state-of-the-art methods in the current literature of metric learning.