Yu-Sheng Chen
Single-Image HDR Reconstruction by Learning to Reverse the Camera Pipeline
Apr 02, 2020



Abstract:Recovering a high dynamic range (HDR) image from a single low dynamic range (LDR) input image is challenging due to missing details in under-/over-exposed regions caused by quantization and saturation of camera sensors. In contrast to existing learning-based methods, our core idea is to incorporate the domain knowledge of the LDR image formation pipeline into our model. We model the HDRto-LDR image formation pipeline as the (1) dynamic range clipping, (2) non-linear mapping from a camera response function, and (3) quantization. We then propose to learn three specialized CNNs to reverse these steps. By decomposing the problem into specific sub-tasks, we impose effective physical constraints to facilitate the training of individual sub-networks. Finally, we jointly fine-tune the entire model end-to-end to reduce error accumulation. With extensive quantitative and qualitative experiments on diverse image datasets, we demonstrate that the proposed method performs favorably against state-of-the-art single-image HDR reconstruction algorithms.
COCO-GAN: Generation by Parts via Conditional Coordinating
Apr 16, 2019



Abstract:Humans can only interact with part of the surrounding environment due to biological restrictions. Therefore, we learn to reason the spatial relationships across a series of observations to piece together the surrounding environment. Inspired by such behavior and the fact that machines also have computational constraints, we propose \underline{CO}nditional \underline{CO}ordinate GAN (COCO-GAN) of which the generator generates images by parts based on their spatial coordinates as the condition. On the other hand, the discriminator learns to justify realism across multiple assembled patches by global coherence, local appearance, and edge-crossing continuity. Despite the full images are never generated during training, we show that COCO-GAN can produce \textbf{state-of-the-art-quality} full images during inference. We further demonstrate a variety of novel applications enabled by teaching the network to be aware of coordinates. First, we perform extrapolation to the learned coordinate manifold and generate off-the-boundary patches. Combining with the originally generated full image, COCO-GAN can produce images that are larger than training samples, which we called "beyond-boundary generation". We then showcase panorama generation within a cylindrical coordinate system that inherently preserves horizontally cyclic topology. On the computation side, COCO-GAN has a built-in divide-and-conquer paradigm that reduces memory requisition during training and inference, provides high-parallelism, and can generate parts of images on-demand.
Learning Deep Convolutional Networks for Demosaicing
Feb 11, 2018



Abstract:This paper presents a comprehensive study of applying the convolutional neural network (CNN) to solving the demosaicing problem. The paper presents two CNN models that learn end-to-end mappings between the mosaic samples and the original image patches with full information. In the case the Bayer color filter array (CFA) is used, an evaluation with ten competitive methods on popular benchmarks confirms that the data-driven, automatically learned features by the CNN models are very effective. Experiments show that the proposed CNN models can perform equally well in both the sRGB space and the linear space. It is also demonstrated that the CNN model can perform joint denoising and demosaicing. The CNN model is very flexible and can be easily adopted for demosaicing with any CFA design. We train CNN models for demosaicing with three different CFAs and obtain better results than existing methods. With the great flexibility to be coupled with any CFA, we present the first data-driven joint optimization of the CFA design and the demosaicing method using CNN. Experiments show that the combination of the automatically discovered CFA pattern and the automatically devised demosaicing method significantly outperforms the current best demosaicing results. Visual comparisons confirm that the proposed methods reduce more visual artifacts than existing methods. Finally, we show that the CNN model is also effective for the more general demosaicing problem with spatially varying exposure and color and can be used for taking images of higher dynamic ranges with a single shot. The proposed models and the thorough experiments together demonstrate that CNN is an effective and versatile tool for solving the demosaicing problem.
A Mathematical Theory for Clustering in Metric Spaces
Sep 25, 2015
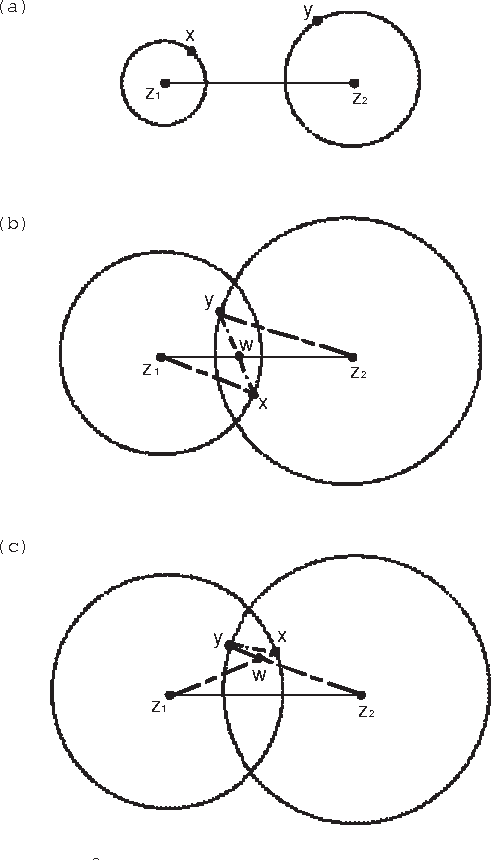
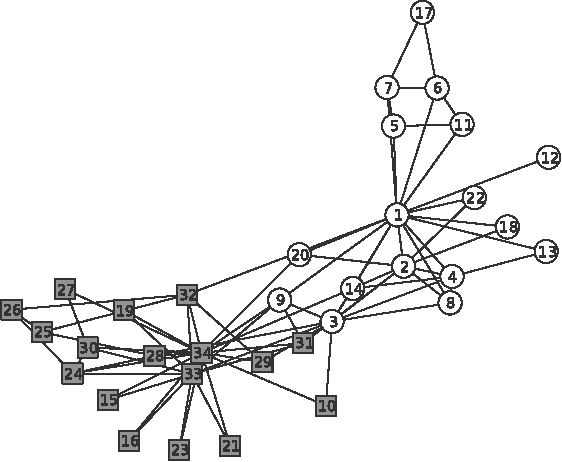
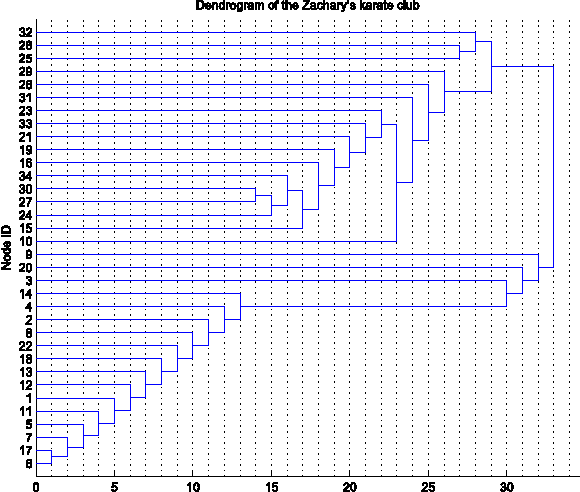
Abstract:Clustering is one of the most fundamental problems in data analysis and it has been studied extensively in the literature. Though many clustering algorithms have been proposed, clustering theories that justify the use of these clustering algorithms are still unsatisfactory. In particular, one of the fundamental challenges is to address the following question: What is a cluster in a set of data points? In this paper, we make an attempt to address such a question by considering a set of data points associated with a distance measure (metric). We first propose a new cohesion measure in terms of the distance measure. Using the cohesion measure, we define a cluster as a set of points that are cohesive to themselves. For such a definition, we show there are various equivalent statements that have intuitive explanations. We then consider the second question: How do we find clusters and good partitions of clusters under such a definition? For such a question, we propose a hierarchical agglomerative algorithm and a partitional algorithm. Unlike standard hierarchical agglomerative algorithms, our hierarchical agglomerative algorithm has a specific stopping criterion and it stops with a partition of clusters. Our partitional algorithm, called the K-sets algorithm in the paper, appears to be a new iterative algorithm. Unlike the Lloyd iteration that needs two-step minimization, our K-sets algorithm only takes one-step minimization. One of the most interesting findings of our paper is the duality result between a distance measure and a cohesion measure. Such a duality result leads to a dual K-sets algorithm for clustering a set of data points with a cohesion measure. The dual K-sets algorithm converges in the same way as a sequential version of the classical kernel K-means algorithm. The key difference is that a cohesion measure does not need to be positive semi-definite.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge