A Mathematical Theory for Learning Semantic Languages by Abstract Learners

Recent advances in Large Language Models (LLMs) have demonstrated the emergence of capabilities (learned skills) when the number of system parameters and the size of training data surpass certain thresholds. The exact mechanisms behind such phenomena are not fully understood and remain a topic of active research. Inspired by the skill-text bipartite graph model presented in [1] for modeling semantic language, we develop a mathematical theory to explain the emergence of learned skills, taking the learning (or training) process into account. Our approach models the learning process for skills in the skill-text bipartite graph as an iterative decoding process in Low-Density Parity Check (LDPC) codes and Irregular Repetition Slotted ALOHA (IRSA). Using density evolution analysis, we demonstrate the emergence of learned skills when the ratio of the size of training texts to the number of skills exceeds a certain threshold. Our analysis also yields a scaling law for testing errors relative to the size of training texts. Upon completion of the training, we propose a method for semantic compression and discuss its application in semantic communication.

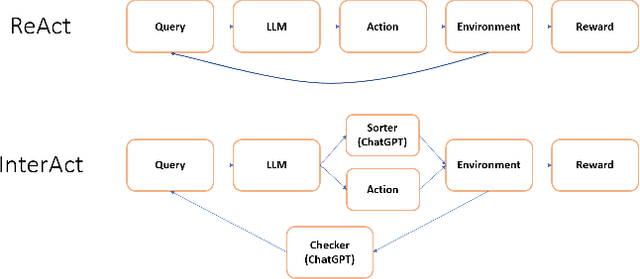
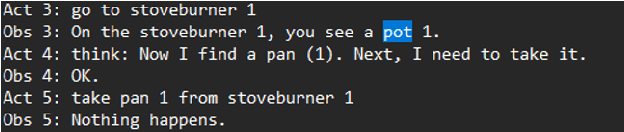
InterAct: Exploring the Potentials of ChatGPT as a Cooperative Agent

This research paper delves into the integration of OpenAI's ChatGPT into embodied agent systems, evaluating its influence on interactive decision-making benchmark. Drawing a parallel to the concept of people assuming roles according to their unique strengths, we introduce InterAct. In this approach, we feed ChatGPT with varied prompts, assigning it a numerous roles like a checker and a sorter, then integrating them with the original language model. Our research shows a remarkable success rate of 98% in AlfWorld, which consists of 6 different tasks in a simulated household environment, emphasizing the significance of proficient prompt engineering. The results highlight ChatGPT's competence in comprehending and performing intricate tasks effectively in real-world settings, thus paving the way for further advancements in task planning.

A Simple Explanation for the Phase Transition in Large Language Models with List Decoding

Various recent experimental results show that large language models (LLM) exhibit emergent abilities that are not present in small models. System performance is greatly improved after passing a certain critical threshold of scale. In this letter, we provide a simple explanation for such a phase transition phenomenon. For this, we model an LLM as a sequence-to-sequence random function. Instead of using instant generation at each step, we use a list decoder that keeps a list of candidate sequences at each step and defers the generation of the output sequence at the end. We show that there is a critical threshold such that the expected number of erroneous candidate sequences remains bounded when an LLM is below the threshold, and it grows exponentially when an LLM is above the threshold. Such a threshold is related to the basic reproduction number in a contagious disease.

Explainable, Stable, and Scalable Graph Convolutional Networks for Learning Graph Representation

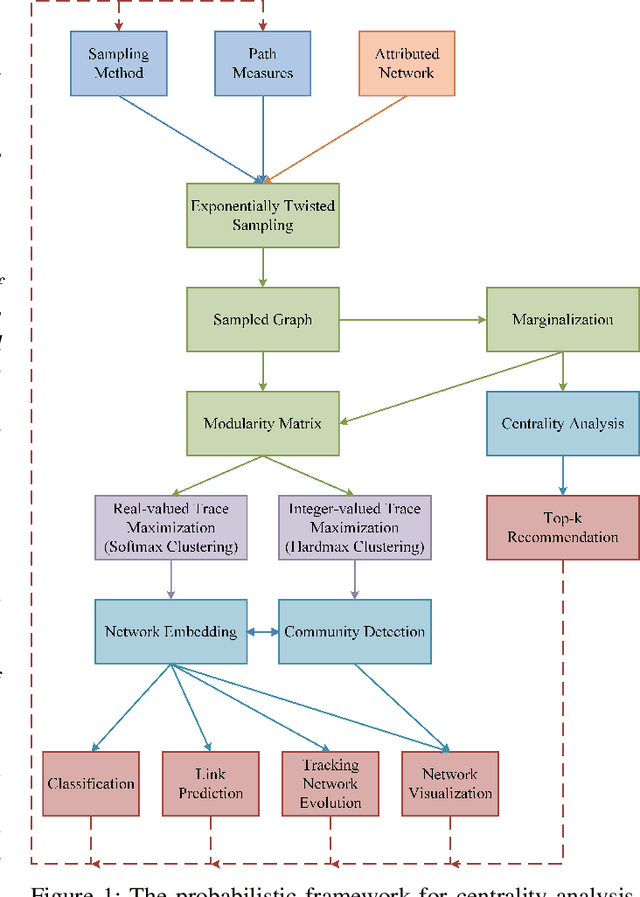
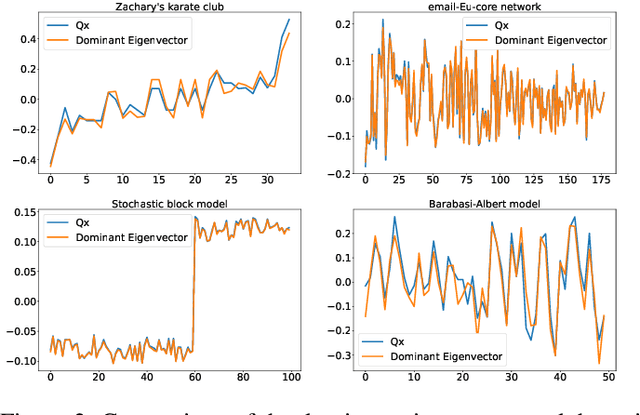
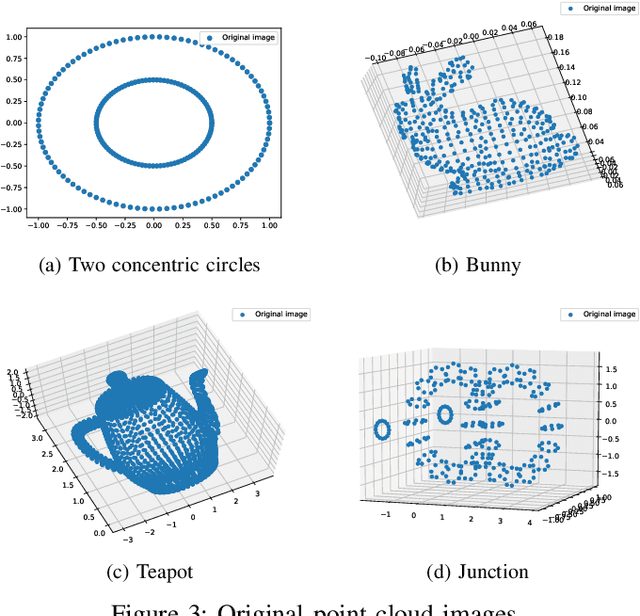
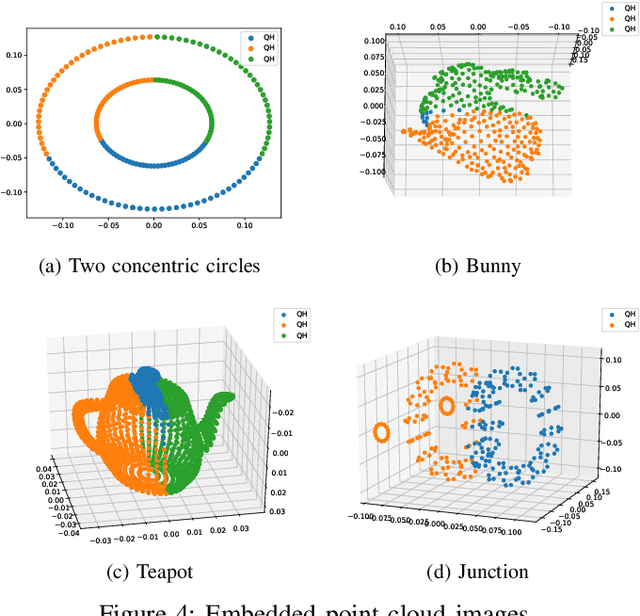
The network embedding problem that maps nodes in a graph to vectors in Euclidean space can be very useful for addressing several important tasks on a graph. Recently, graph neural networks (GNNs) have been proposed for solving such a problem. However, most embedding algorithms and GNNs are difficult to interpret and do not scale well to handle millions of nodes. In this paper, we tackle the problem from a new perspective based on the equivalence of three constrained optimization problems: the network embedding problem, the trace maximization problem of the modularity matrix in a sampled graph, and the matrix factorization problem of the modularity matrix in a sampled graph. The optimal solutions to these three problems are the dominant eigenvectors of the modularity matrix. We proposed two algorithms that belong to a special class of graph convolutional networks (GCNs) for solving these problems: (i) Clustering As Feature Embedding GCN (CAFE-GCN) and (ii) sphere-GCN. Both algorithms are stable trace maximization algorithms, and they yield good approximations of dominant eigenvectors. Moreover, there are linear-time implementations for sparse graphs. In addition to solving the network embedding problem, both proposed GCNs are capable of performing dimensionality reduction. Various experiments are conducted to evaluate our proposed GCNs and show that our proposed GCNs outperform almost all the baseline methods. Moreover, CAFE-GCN could be benefited from the labeled data and have tremendous improvements in various performance metrics.

A Time-dependent SIR model for COVID-19

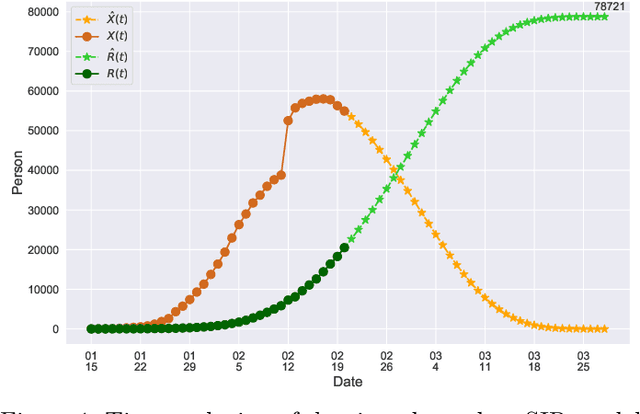
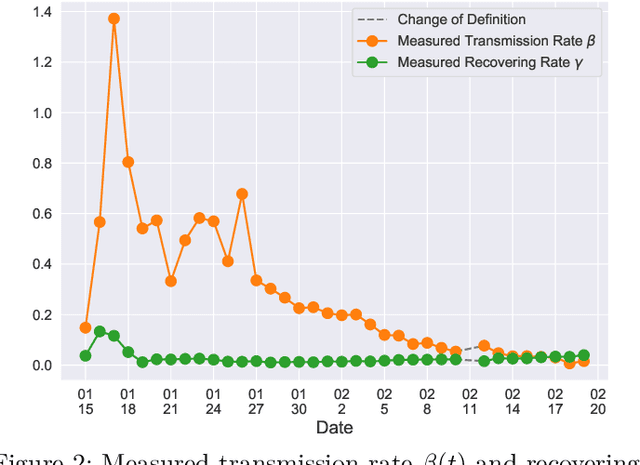
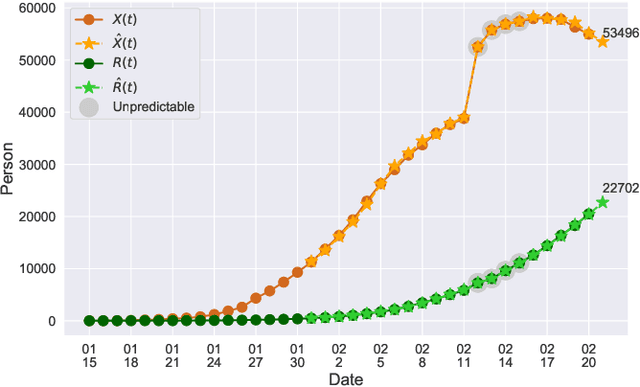
In this paper, we propose a mathematical model for analyzing and predicting the number of confirmed cases of COVID-19. Our model is a time-dependent susceptible-infected-recovered (SIR) model that tracks two time series: (i) the transmission rate at time $t$ and (ii) the recovering rate at time $t$. Our time-dependent SIR method is better than the traditional static SIR model as it can adapt to the change of contagious disease control policies such as city lockdowns. Moreover, it is also more robust than the direct estimation of the number of confirmed cases, as a sudden change of the definition of the number of confirmed cases might result in a spike of the number of new cases. Using the data set provided by the National Health Commission of the People's Republic of China (NHC) [2], we show that the one-day prediction errors for the numbers of confirmed cases are less than $3\%$ except the day when the definition of the number of confirmed cases is changed. Also, the turning point, defined as the day that the transmission rate is less than the recovering rate, is predicted to be Feb. 17, 2020. After that day, the basic reproduction number, known as the $R_0(t)$ value, is less than $1$ if the current contagious disease control policies are maintained in China. In that case, the total number of confirmed cases is predicted to be less than $80,000$ cases in China under our deterministic model.

A Reinforcement Learning Approach for the Multichannel Rendezvous Problem

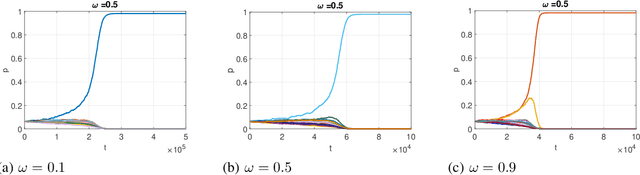
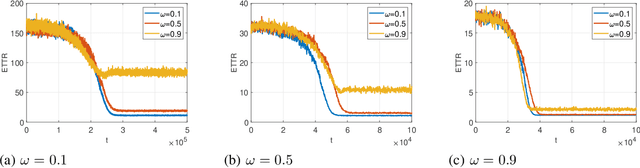
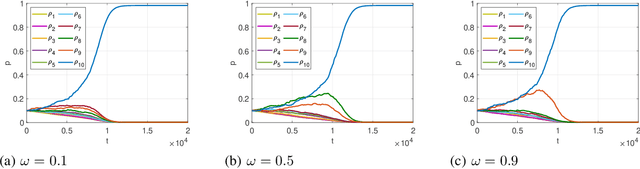
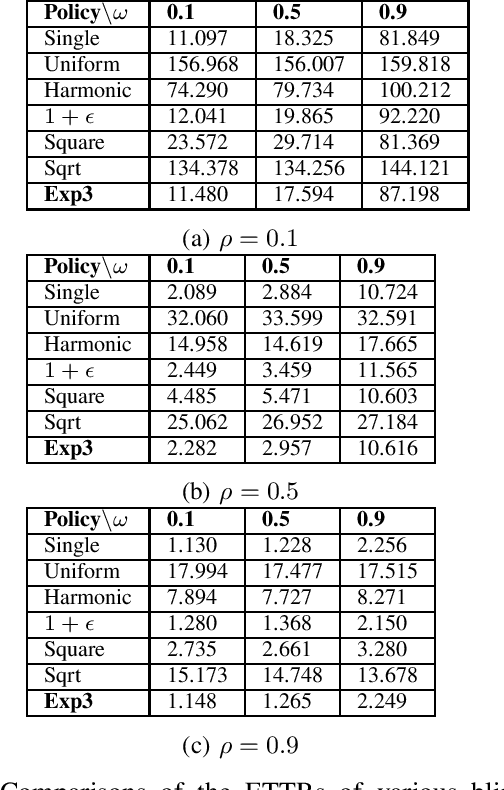
In this paper, we consider the multichannel rendezvous problem in cognitive radio networks (CRNs) where the probability that two users hopping on the same channel have a successful rendezvous is a function of channel states. The channel states are modelled by two-state Markov chains that have a good state and a bad state. These channel states are not observable by the users. For such a multichannel rendezvous problem, we are interested in finding the optimal policy to minimize the expected time-to-rendezvous (ETTR) among the class of {\em dynamic blind rendezvous policies}, i.e., at the $t^{th}$ time slot each user selects channel $i$ independently with probability $p_i(t)$, $i=1,2, \ldots, N$. By formulating such a multichannel rendezvous problem as an adversarial bandit problem, we propose using a reinforcement learning approach to learn the channel selection probabilities $p_i(t)$, $i=1,2, \ldots, N$. Our experimental results show that the reinforcement learning approach is very effective and yields comparable ETTRs when comparing to various approximation policies in the literature.

K-sets+: a Linear-time Clustering Algorithm for Data Points with a Sparse Similarity Measure

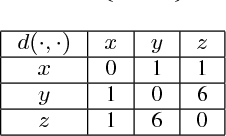
In this paper, we first propose a new iterative algorithm, called the K-sets+ algorithm for clustering data points in a semi-metric space, where the distance measure does not necessarily satisfy the triangular inequality. We show that the K-sets+ algorithm converges in a finite number of iterations and it retains the same performance guarantee as the K-sets algorithm for clustering data points in a metric space. We then extend the applicability of the K-sets+ algorithm from data points in a semi-metric space to data points that only have a symmetric similarity measure. Such an extension leads to great reduction of computational complexity. In particular, for an n * n similarity matrix with m nonzero elements in the matrix, the computational complexity of the K-sets+ algorithm is O((Kn + m)I), where I is the number of iterations. The memory complexity to achieve that computational complexity is O(Kn + m). As such, both the computational complexity and the memory complexity are linear in n when the n * n similarity matrix is sparse, i.e., m = O(n). We also conduct various experiments to show the effectiveness of the K-sets+ algorithm by using a synthetic dataset from the stochastic block model and a real network from the WonderNetwork website.

A Mathematical Theory for Clustering in Metric Spaces

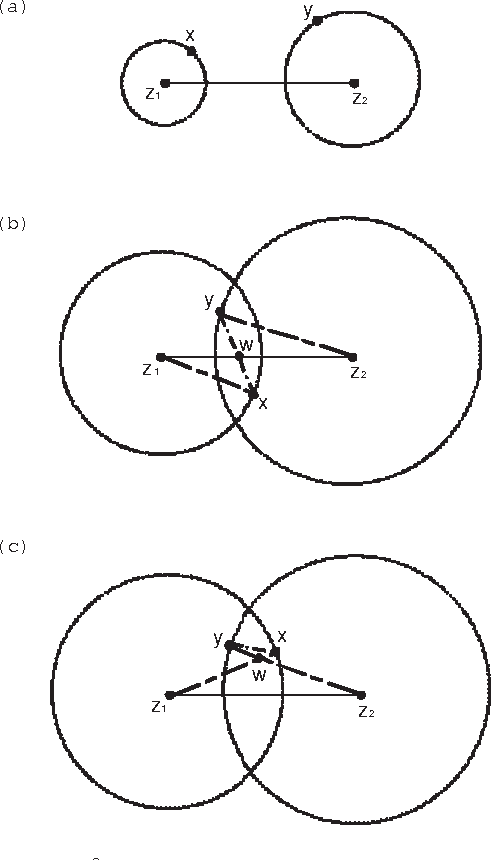
Clustering is one of the most fundamental problems in data analysis and it has been studied extensively in the literature. Though many clustering algorithms have been proposed, clustering theories that justify the use of these clustering algorithms are still unsatisfactory. In particular, one of the fundamental challenges is to address the following question: What is a cluster in a set of data points? In this paper, we make an attempt to address such a question by considering a set of data points associated with a distance measure (metric). We first propose a new cohesion measure in terms of the distance measure. Using the cohesion measure, we define a cluster as a set of points that are cohesive to themselves. For such a definition, we show there are various equivalent statements that have intuitive explanations. We then consider the second question: How do we find clusters and good partitions of clusters under such a definition? For such a question, we propose a hierarchical agglomerative algorithm and a partitional algorithm. Unlike standard hierarchical agglomerative algorithms, our hierarchical agglomerative algorithm has a specific stopping criterion and it stops with a partition of clusters. Our partitional algorithm, called the K-sets algorithm in the paper, appears to be a new iterative algorithm. Unlike the Lloyd iteration that needs two-step minimization, our K-sets algorithm only takes one-step minimization. One of the most interesting findings of our paper is the duality result between a distance measure and a cohesion measure. Such a duality result leads to a dual K-sets algorithm for clustering a set of data points with a cohesion measure. The dual K-sets algorithm converges in the same way as a sequential version of the classical kernel K-means algorithm. The key difference is that a cohesion measure does not need to be positive semi-definite.