K-sets+: a Linear-time Clustering Algorithm for Data Points with a Sparse Similarity Measure

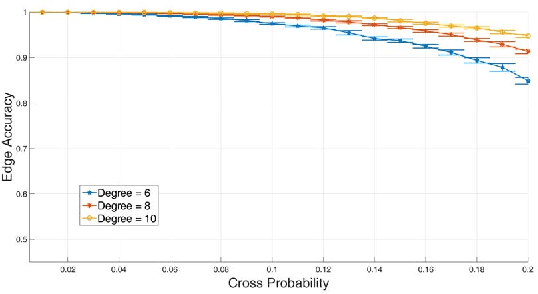
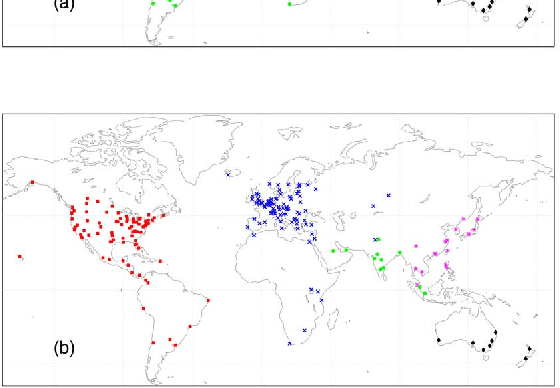
In this paper, we first propose a new iterative algorithm, called the K-sets+ algorithm for clustering data points in a semi-metric space, where the distance measure does not necessarily satisfy the triangular inequality. We show that the K-sets+ algorithm converges in a finite number of iterations and it retains the same performance guarantee as the K-sets algorithm for clustering data points in a metric space. We then extend the applicability of the K-sets+ algorithm from data points in a semi-metric space to data points that only have a symmetric similarity measure. Such an extension leads to great reduction of computational complexity. In particular, for an n * n similarity matrix with m nonzero elements in the matrix, the computational complexity of the K-sets+ algorithm is O((Kn + m)I), where I is the number of iterations. The memory complexity to achieve that computational complexity is O(Kn + m). As such, both the computational complexity and the memory complexity are linear in n when the n * n similarity matrix is sparse, i.e., m = O(n). We also conduct various experiments to show the effectiveness of the K-sets+ algorithm by using a synthetic dataset from the stochastic block model and a real network from the WonderNetwork website.

A Mathematical Theory for Clustering in Metric Spaces

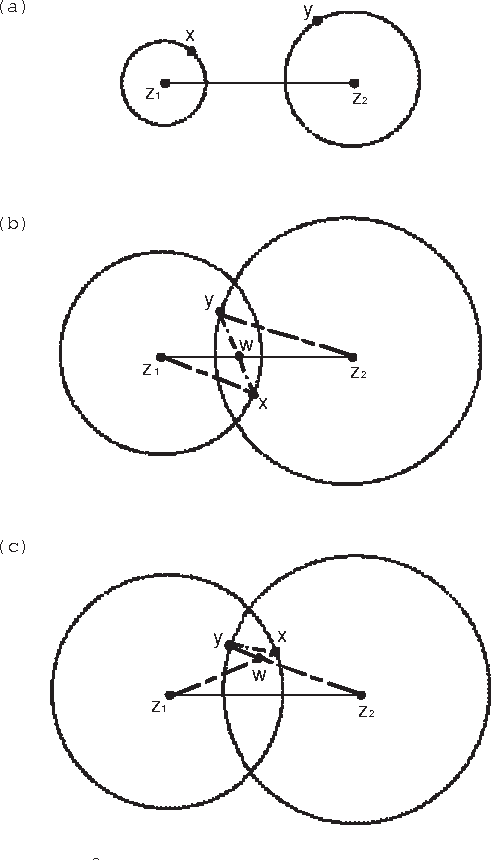
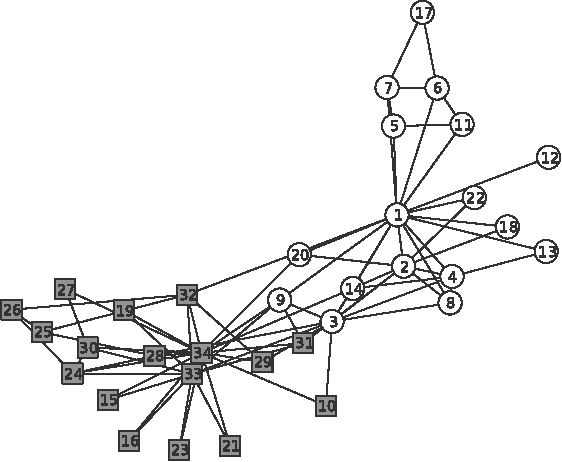
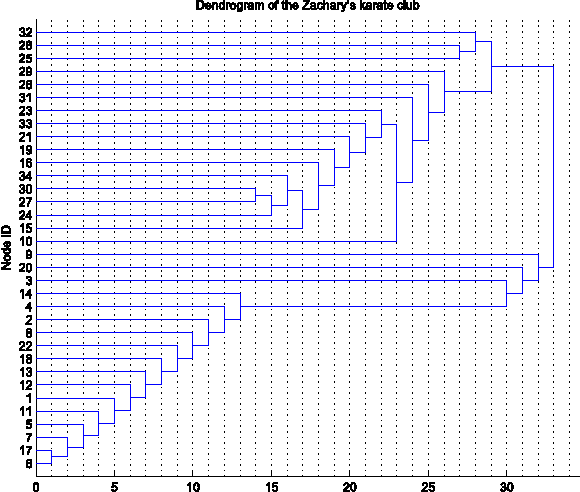
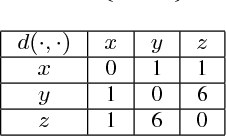
Clustering is one of the most fundamental problems in data analysis and it has been studied extensively in the literature. Though many clustering algorithms have been proposed, clustering theories that justify the use of these clustering algorithms are still unsatisfactory. In particular, one of the fundamental challenges is to address the following question: What is a cluster in a set of data points? In this paper, we make an attempt to address such a question by considering a set of data points associated with a distance measure (metric). We first propose a new cohesion measure in terms of the distance measure. Using the cohesion measure, we define a cluster as a set of points that are cohesive to themselves. For such a definition, we show there are various equivalent statements that have intuitive explanations. We then consider the second question: How do we find clusters and good partitions of clusters under such a definition? For such a question, we propose a hierarchical agglomerative algorithm and a partitional algorithm. Unlike standard hierarchical agglomerative algorithms, our hierarchical agglomerative algorithm has a specific stopping criterion and it stops with a partition of clusters. Our partitional algorithm, called the K-sets algorithm in the paper, appears to be a new iterative algorithm. Unlike the Lloyd iteration that needs two-step minimization, our K-sets algorithm only takes one-step minimization. One of the most interesting findings of our paper is the duality result between a distance measure and a cohesion measure. Such a duality result leads to a dual K-sets algorithm for clustering a set of data points with a cohesion measure. The dual K-sets algorithm converges in the same way as a sequential version of the classical kernel K-means algorithm. The key difference is that a cohesion measure does not need to be positive semi-definite.