A Reinforcement Learning Approach for the Multichannel Rendezvous Problem

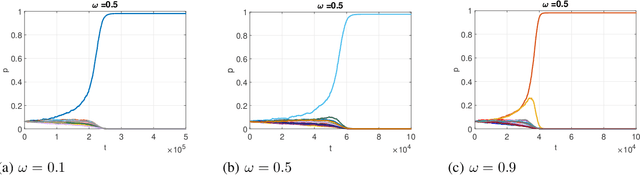
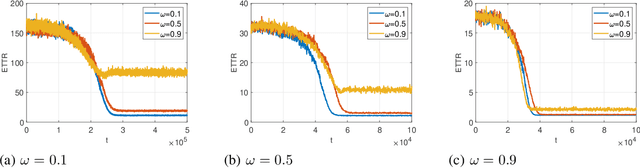
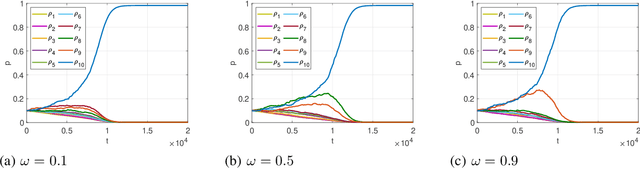
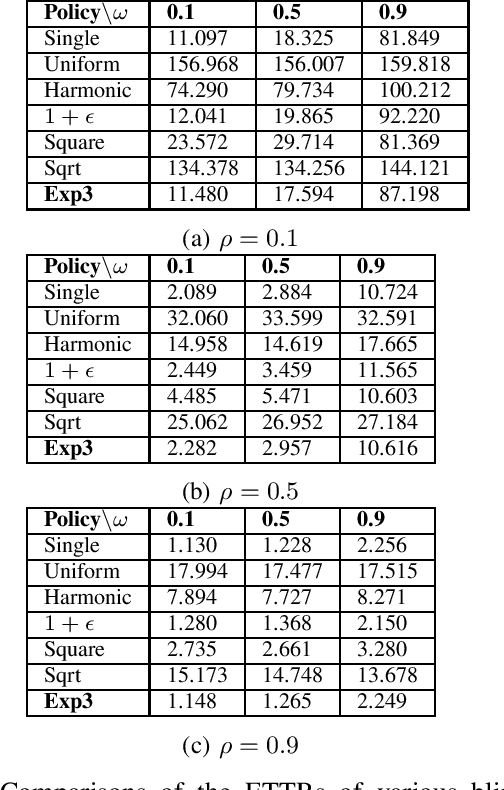
In this paper, we consider the multichannel rendezvous problem in cognitive radio networks (CRNs) where the probability that two users hopping on the same channel have a successful rendezvous is a function of channel states. The channel states are modelled by two-state Markov chains that have a good state and a bad state. These channel states are not observable by the users. For such a multichannel rendezvous problem, we are interested in finding the optimal policy to minimize the expected time-to-rendezvous (ETTR) among the class of {\em dynamic blind rendezvous policies}, i.e., at the $t^{th}$ time slot each user selects channel $i$ independently with probability $p_i(t)$, $i=1,2, \ldots, N$. By formulating such a multichannel rendezvous problem as an adversarial bandit problem, we propose using a reinforcement learning approach to learn the channel selection probabilities $p_i(t)$, $i=1,2, \ldots, N$. Our experimental results show that the reinforcement learning approach is very effective and yields comparable ETTRs when comparing to various approximation policies in the literature.

K-sets+: a Linear-time Clustering Algorithm for Data Points with a Sparse Similarity Measure

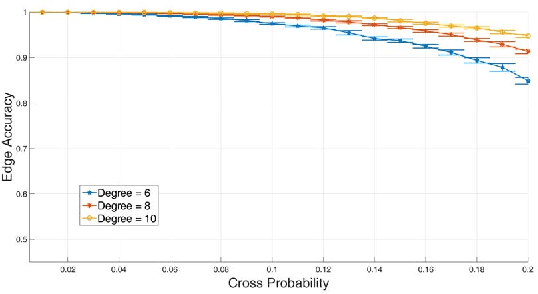
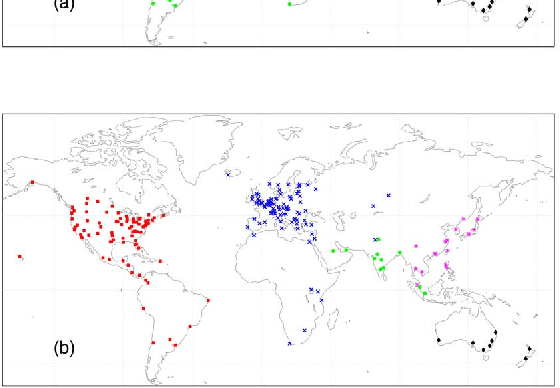
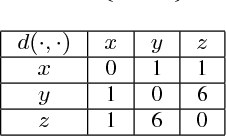
In this paper, we first propose a new iterative algorithm, called the K-sets+ algorithm for clustering data points in a semi-metric space, where the distance measure does not necessarily satisfy the triangular inequality. We show that the K-sets+ algorithm converges in a finite number of iterations and it retains the same performance guarantee as the K-sets algorithm for clustering data points in a metric space. We then extend the applicability of the K-sets+ algorithm from data points in a semi-metric space to data points that only have a symmetric similarity measure. Such an extension leads to great reduction of computational complexity. In particular, for an n * n similarity matrix with m nonzero elements in the matrix, the computational complexity of the K-sets+ algorithm is O((Kn + m)I), where I is the number of iterations. The memory complexity to achieve that computational complexity is O(Kn + m). As such, both the computational complexity and the memory complexity are linear in n when the n * n similarity matrix is sparse, i.e., m = O(n). We also conduct various experiments to show the effectiveness of the K-sets+ algorithm by using a synthetic dataset from the stochastic block model and a real network from the WonderNetwork website.