A Reinforcement Learning Approach for the Multichannel Rendezvous Problem
Paper and Code
Jul 05, 2019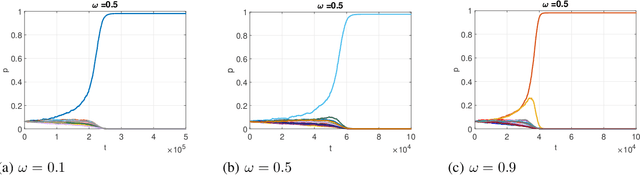
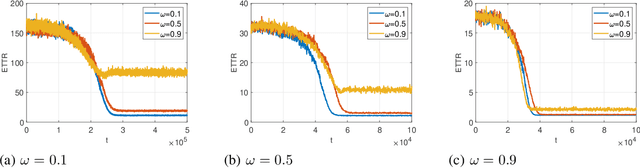
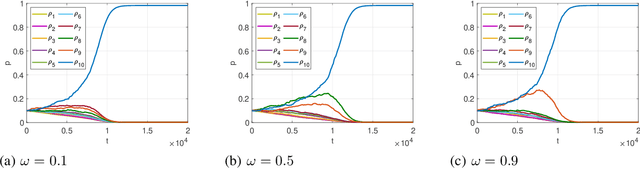
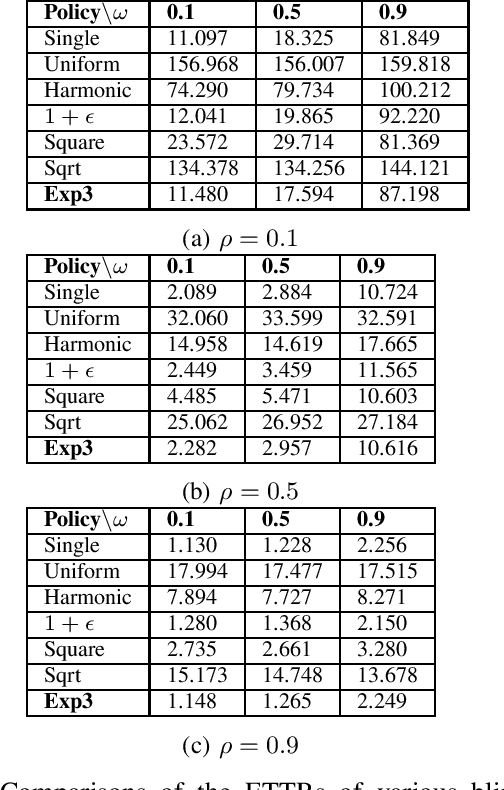
In this paper, we consider the multichannel rendezvous problem in cognitive radio networks (CRNs) where the probability that two users hopping on the same channel have a successful rendezvous is a function of channel states. The channel states are modelled by two-state Markov chains that have a good state and a bad state. These channel states are not observable by the users. For such a multichannel rendezvous problem, we are interested in finding the optimal policy to minimize the expected time-to-rendezvous (ETTR) among the class of {\em dynamic blind rendezvous policies}, i.e., at the $t^{th}$ time slot each user selects channel $i$ independently with probability $p_i(t)$, $i=1,2, \ldots, N$. By formulating such a multichannel rendezvous problem as an adversarial bandit problem, we propose using a reinforcement learning approach to learn the channel selection probabilities $p_i(t)$, $i=1,2, \ldots, N$. Our experimental results show that the reinforcement learning approach is very effective and yields comparable ETTRs when comparing to various approximation policies in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge