Explainable, Stable, and Scalable Graph Convolutional Networks for Learning Graph Representation

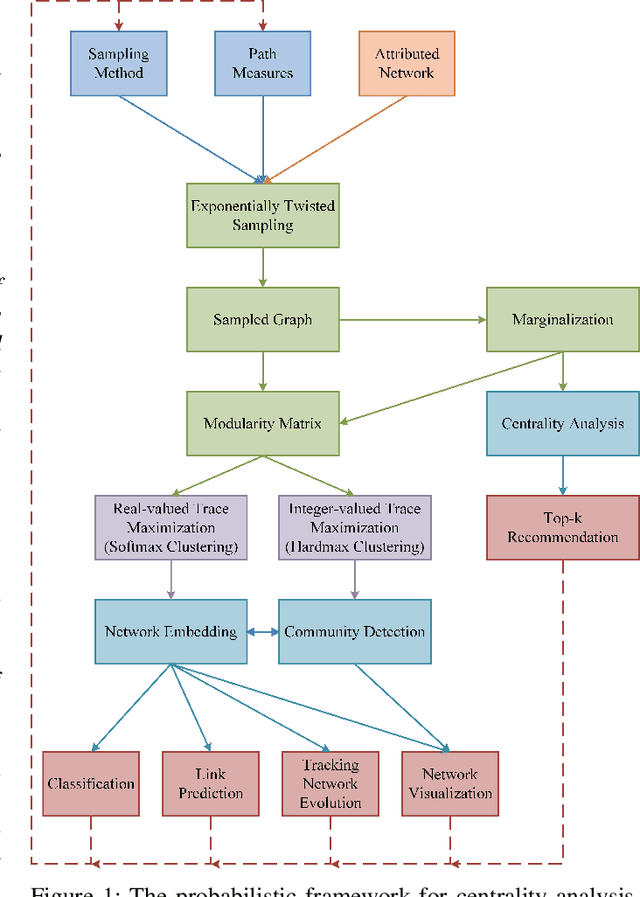
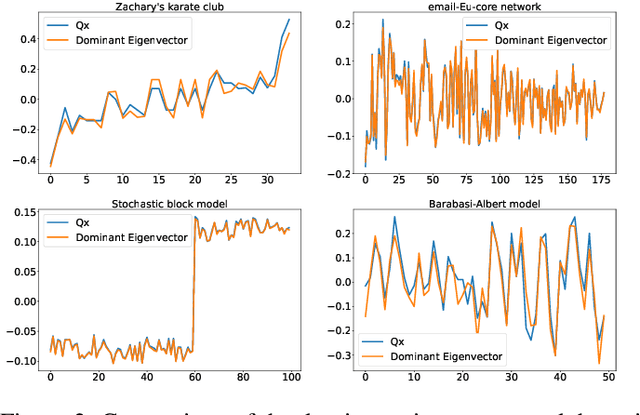
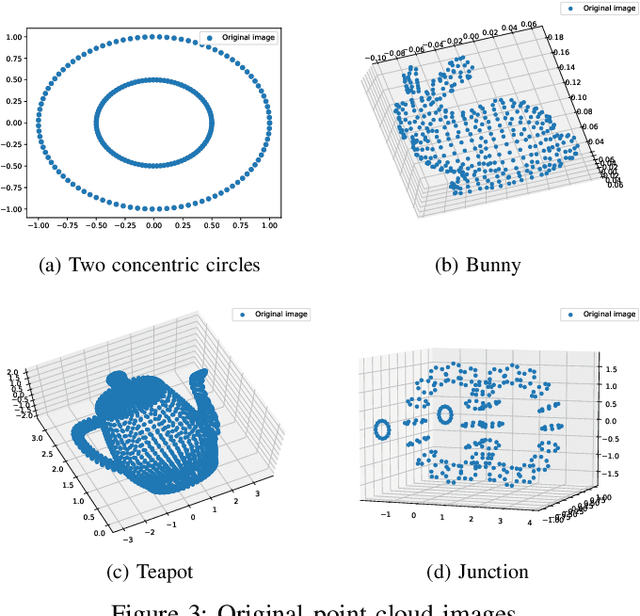
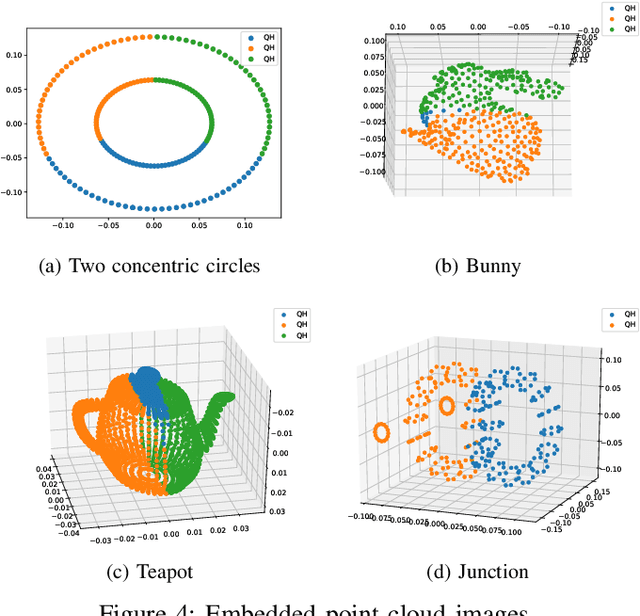
The network embedding problem that maps nodes in a graph to vectors in Euclidean space can be very useful for addressing several important tasks on a graph. Recently, graph neural networks (GNNs) have been proposed for solving such a problem. However, most embedding algorithms and GNNs are difficult to interpret and do not scale well to handle millions of nodes. In this paper, we tackle the problem from a new perspective based on the equivalence of three constrained optimization problems: the network embedding problem, the trace maximization problem of the modularity matrix in a sampled graph, and the matrix factorization problem of the modularity matrix in a sampled graph. The optimal solutions to these three problems are the dominant eigenvectors of the modularity matrix. We proposed two algorithms that belong to a special class of graph convolutional networks (GCNs) for solving these problems: (i) Clustering As Feature Embedding GCN (CAFE-GCN) and (ii) sphere-GCN. Both algorithms are stable trace maximization algorithms, and they yield good approximations of dominant eigenvectors. Moreover, there are linear-time implementations for sparse graphs. In addition to solving the network embedding problem, both proposed GCNs are capable of performing dimensionality reduction. Various experiments are conducted to evaluate our proposed GCNs and show that our proposed GCNs outperform almost all the baseline methods. Moreover, CAFE-GCN could be benefited from the labeled data and have tremendous improvements in various performance metrics.

A Time-dependent SIR model for COVID-19

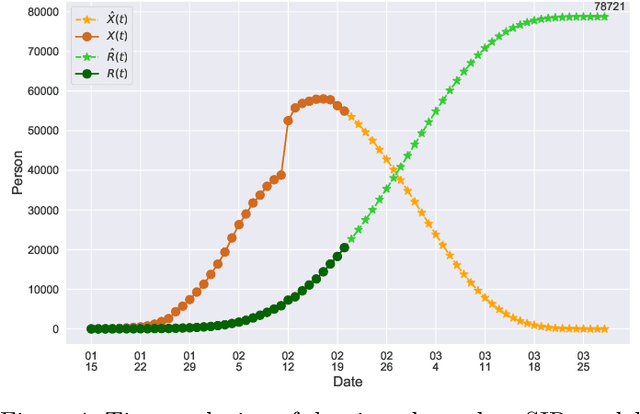
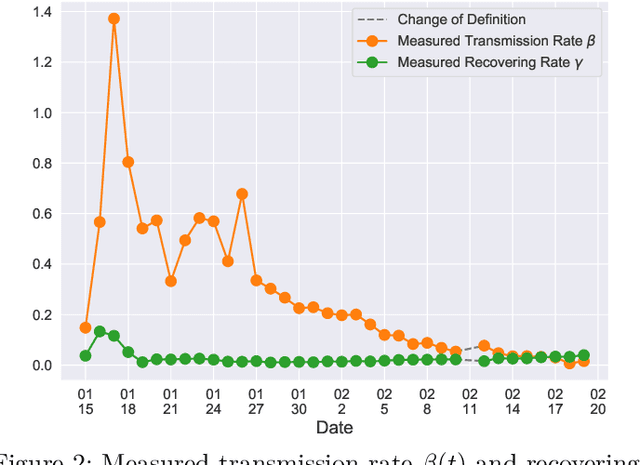
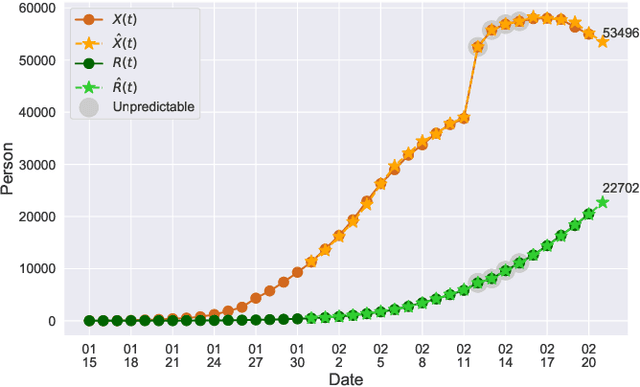
In this paper, we propose a mathematical model for analyzing and predicting the number of confirmed cases of COVID-19. Our model is a time-dependent susceptible-infected-recovered (SIR) model that tracks two time series: (i) the transmission rate at time $t$ and (ii) the recovering rate at time $t$. Our time-dependent SIR method is better than the traditional static SIR model as it can adapt to the change of contagious disease control policies such as city lockdowns. Moreover, it is also more robust than the direct estimation of the number of confirmed cases, as a sudden change of the definition of the number of confirmed cases might result in a spike of the number of new cases. Using the data set provided by the National Health Commission of the People's Republic of China (NHC) [2], we show that the one-day prediction errors for the numbers of confirmed cases are less than $3\%$ except the day when the definition of the number of confirmed cases is changed. Also, the turning point, defined as the day that the transmission rate is less than the recovering rate, is predicted to be Feb. 17, 2020. After that day, the basic reproduction number, known as the $R_0(t)$ value, is less than $1$ if the current contagious disease control policies are maintained in China. In that case, the total number of confirmed cases is predicted to be less than $80,000$ cases in China under our deterministic model.

A Reinforcement Learning Approach for the Multichannel Rendezvous Problem

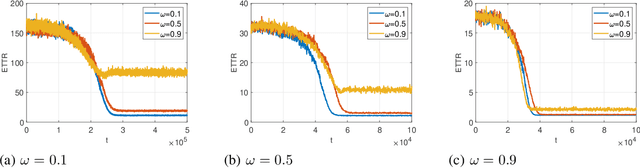
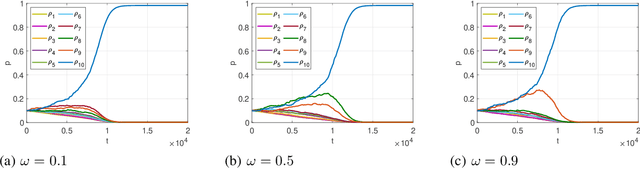
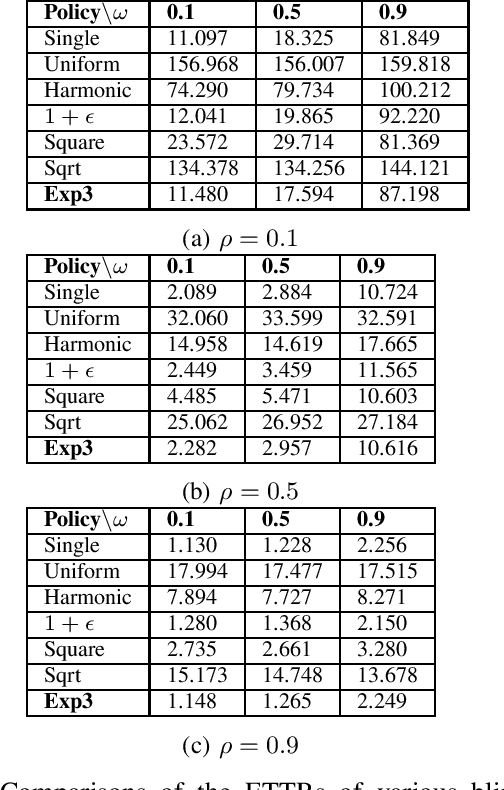
In this paper, we consider the multichannel rendezvous problem in cognitive radio networks (CRNs) where the probability that two users hopping on the same channel have a successful rendezvous is a function of channel states. The channel states are modelled by two-state Markov chains that have a good state and a bad state. These channel states are not observable by the users. For such a multichannel rendezvous problem, we are interested in finding the optimal policy to minimize the expected time-to-rendezvous (ETTR) among the class of {\em dynamic blind rendezvous policies}, i.e., at the $t^{th}$ time slot each user selects channel $i$ independently with probability $p_i(t)$, $i=1,2, \ldots, N$. By formulating such a multichannel rendezvous problem as an adversarial bandit problem, we propose using a reinforcement learning approach to learn the channel selection probabilities $p_i(t)$, $i=1,2, \ldots, N$. Our experimental results show that the reinforcement learning approach is very effective and yields comparable ETTRs when comparing to various approximation policies in the literature.