Chia-Tai Chang
K-sets+: a Linear-time Clustering Algorithm for Data Points with a Sparse Similarity Measure
May 11, 2017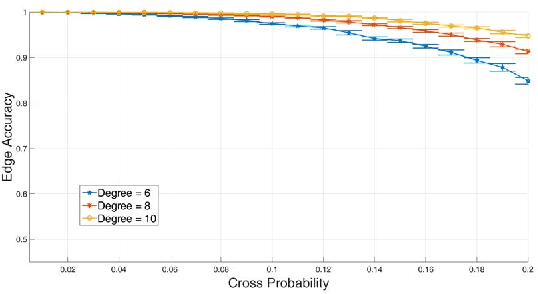
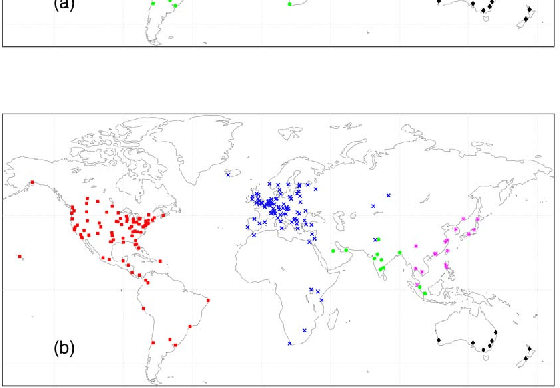
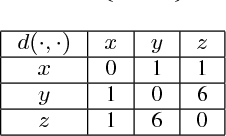
Abstract:In this paper, we first propose a new iterative algorithm, called the K-sets+ algorithm for clustering data points in a semi-metric space, where the distance measure does not necessarily satisfy the triangular inequality. We show that the K-sets+ algorithm converges in a finite number of iterations and it retains the same performance guarantee as the K-sets algorithm for clustering data points in a metric space. We then extend the applicability of the K-sets+ algorithm from data points in a semi-metric space to data points that only have a symmetric similarity measure. Such an extension leads to great reduction of computational complexity. In particular, for an n * n similarity matrix with m nonzero elements in the matrix, the computational complexity of the K-sets+ algorithm is O((Kn + m)I), where I is the number of iterations. The memory complexity to achieve that computational complexity is O(Kn + m). As such, both the computational complexity and the memory complexity are linear in n when the n * n similarity matrix is sparse, i.e., m = O(n). We also conduct various experiments to show the effectiveness of the K-sets+ algorithm by using a synthetic dataset from the stochastic block model and a real network from the WonderNetwork website.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge