A general reduced-order neural operator for spatio-temporal predictive learning on complex spatial domains

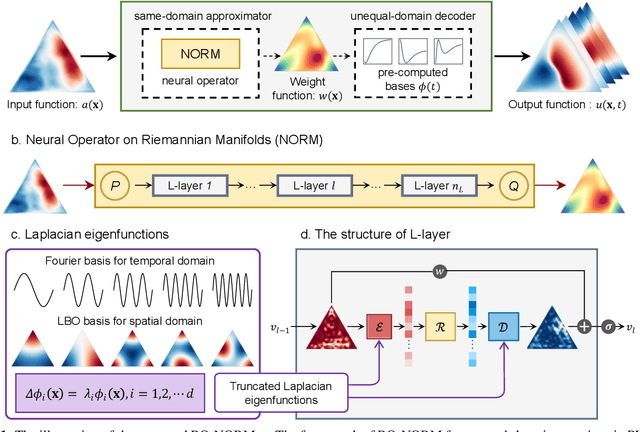
Predictive learning for spatio-temporal processes (PL-STP) on complex spatial domains plays a critical role in various scientific and engineering fields, with its essence being the construction of operators between infinite-dimensional function spaces. This paper focuses on the unequal-domain mappings in PL-STP and categorising them into increase-domain and decrease-domain mapping. Recent advances in deep learning have revealed the great potential of neural operators (NOs) to learn operators directly from observational data. However, existing NOs require input space and output space to be the same domain, which pose challenges in ensuring predictive accuracy and stability for unequal-domain mappings. To this end, this study presents a general reduced-order neural operator named Reduced-Order Neural Operator on Riemannian Manifolds (RO-NORM), which consists of two parts: the unequal-domain encoder/decoder and the same-domain approximator. Motivated by the variable separation in classical modal decomposition, the unequal-domain encoder/decoder uses the pre-computed bases to reformulate the spatio-temporal function as a sum of products between spatial (or temporal) bases and corresponding temporally (or spatially) distributed weight functions, thus the original unequal-domain mapping can be converted into a same-domain mapping. Consequently, the same-domain approximator NORM is applied to model the transformed mapping. The performance of our proposed method has been evaluated on six benchmark cases, including parametric PDEs, engineering and biomedical applications, and compared with four baseline algorithms: DeepONet, POD-DeepONet, PCA-Net, and vanilla NORM. The experimental results demonstrate the superiority of RO-NORM in prediction accuracy and training efficiency for PL-STP.

Diffeomorphism Neural Operator for various domains and parameters of partial differential equations

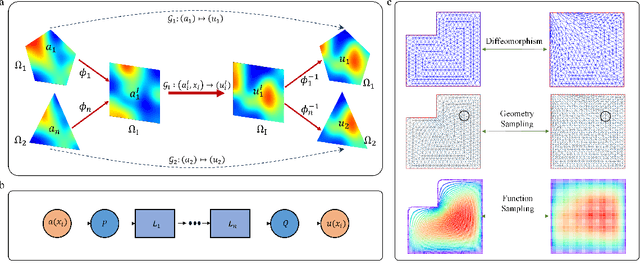
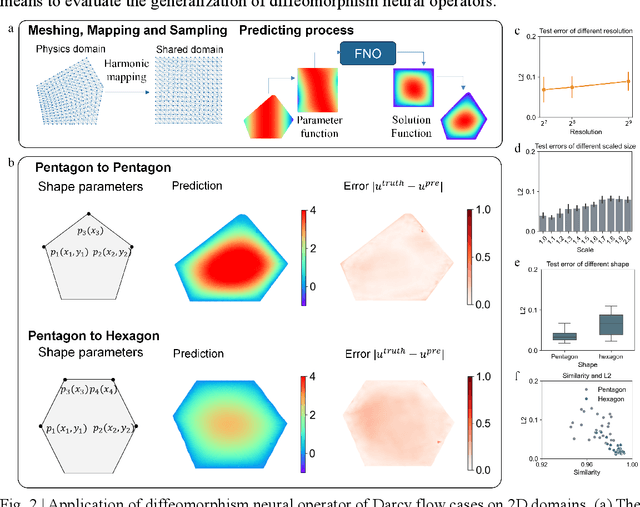
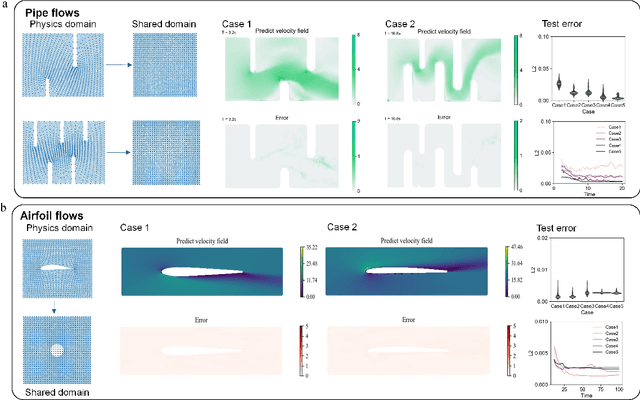
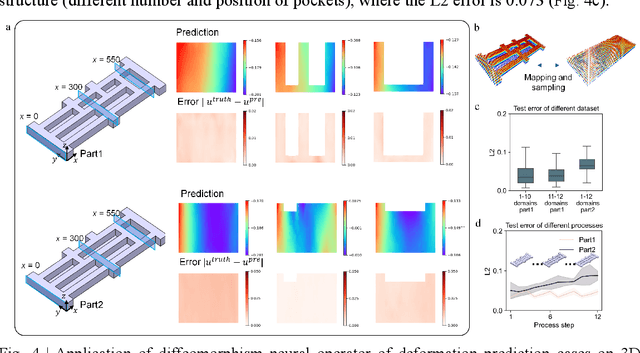
Many science and engineering applications demand partial differential equations (PDE) evaluations that are traditionally computed with resource-intensive numerical solvers. Neural operator models provide an efficient alternative by learning the governing physical laws directly from data in a class of PDEs with different parameters, but constrained in a fixed boundary (domain). Many applications, such as design and manufacturing, would benefit from neural operators with flexible domains when studied at scale. Here we present a diffeomorphism neural operator learning framework towards developing domain-flexible models for physical systems with various and complex domains. Specifically, a neural operator trained in a shared domain mapped from various domains of fields by diffeomorphism is proposed, which transformed the problem of learning function mappings in varying domains (spaces) into the problem of learning operators on a shared diffeomorphic domain. Meanwhile, an index is provided to evaluate the generalization of diffeomorphism neural operators in different domains by the domain diffeomorphism similarity. Experiments on statics scenarios (Darcy flow, mechanics) and dynamic scenarios (pipe flow, airfoil flow) demonstrate the advantages of our approach for neural operator learning under various domains, where harmonic and volume parameterization are used as the diffeomorphism for 2D and 3D domains. Our diffeomorphism neural operator approach enables strong learning capability and robust generalization across varying domains and parameters.

Residual fourier neural operator for thermochemical curing of composites

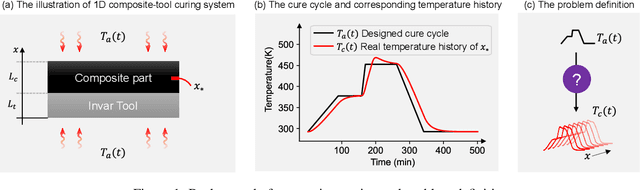
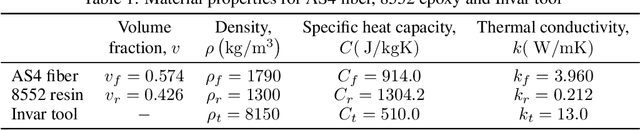
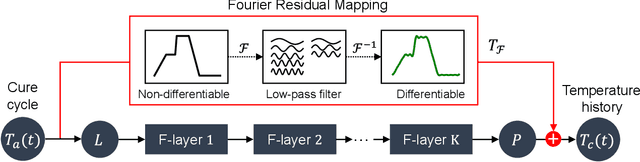
During the curing process of composites, the temperature history heavily determines the evolutions of the field of degree of cure as well as the residual stress, which will further influence the mechanical properties of composite, thus it is important to simulate the real temperature history to optimize the curing process of composites. Since thermochemical analysis using Finite Element (FE) simulations requires heavy computational loads and data-driven approaches suffer from the complexity of highdimensional mapping. This paper proposes a Residual Fourier Neural Operator (ResFNO) to establish the direct high-dimensional mapping from any given cure cycle to the corresponding temperature histories. By integrating domain knowledge into a time-resolution independent parameterized neural network, the mapping between cure cycles to temperature histories can be learned using limited number of labelled data. Besides, a novel Fourier residual mapping is designed based on mode decomposition to accelerate the training and boost the performance significantly. Several cases are carried out to evaluate the superior performance and generalizability of the proposed method comprehensively.