Diffeomorphism Neural Operator for various domains and parameters of partial differential equations
Paper and Code
Feb 19, 2024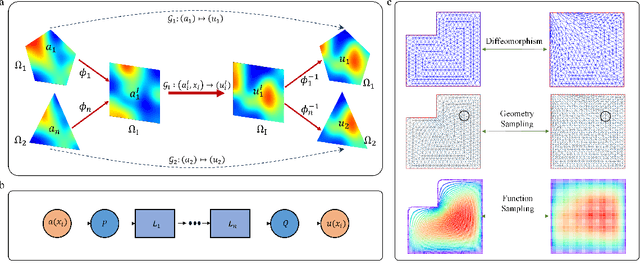
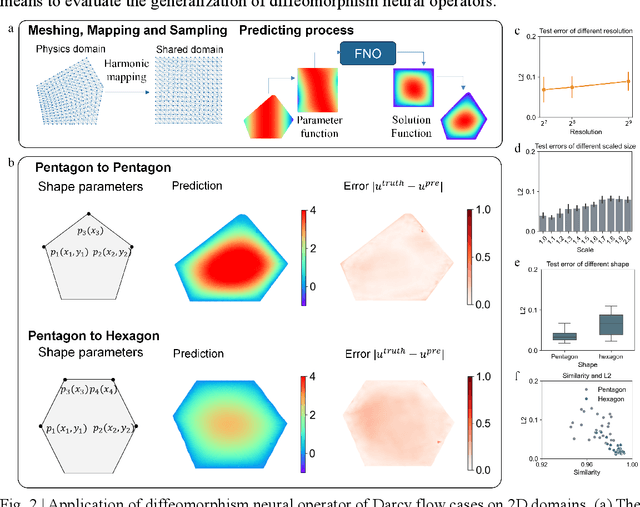
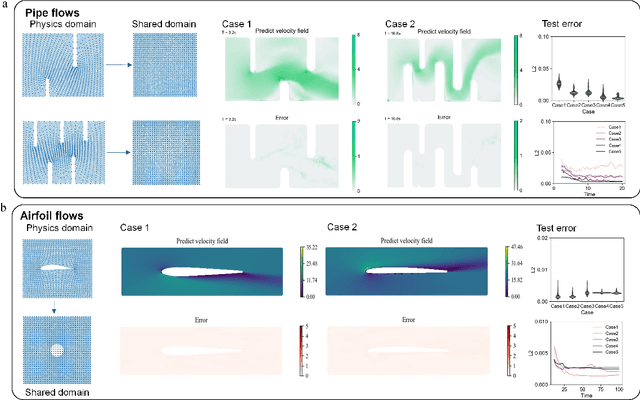
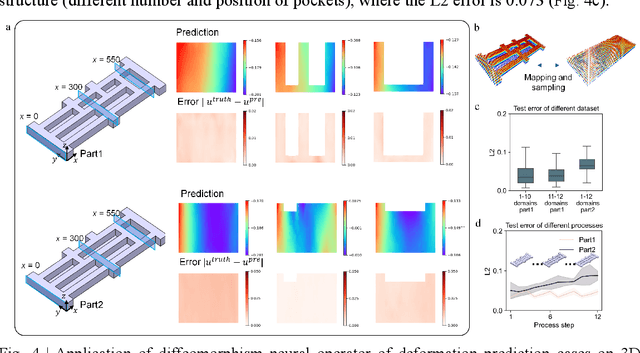
Many science and engineering applications demand partial differential equations (PDE) evaluations that are traditionally computed with resource-intensive numerical solvers. Neural operator models provide an efficient alternative by learning the governing physical laws directly from data in a class of PDEs with different parameters, but constrained in a fixed boundary (domain). Many applications, such as design and manufacturing, would benefit from neural operators with flexible domains when studied at scale. Here we present a diffeomorphism neural operator learning framework towards developing domain-flexible models for physical systems with various and complex domains. Specifically, a neural operator trained in a shared domain mapped from various domains of fields by diffeomorphism is proposed, which transformed the problem of learning function mappings in varying domains (spaces) into the problem of learning operators on a shared diffeomorphic domain. Meanwhile, an index is provided to evaluate the generalization of diffeomorphism neural operators in different domains by the domain diffeomorphism similarity. Experiments on statics scenarios (Darcy flow, mechanics) and dynamic scenarios (pipe flow, airfoil flow) demonstrate the advantages of our approach for neural operator learning under various domains, where harmonic and volume parameterization are used as the diffeomorphism for 2D and 3D domains. Our diffeomorphism neural operator approach enables strong learning capability and robust generalization across varying domains and parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge