A general reduced-order neural operator for spatio-temporal predictive learning on complex spatial domains

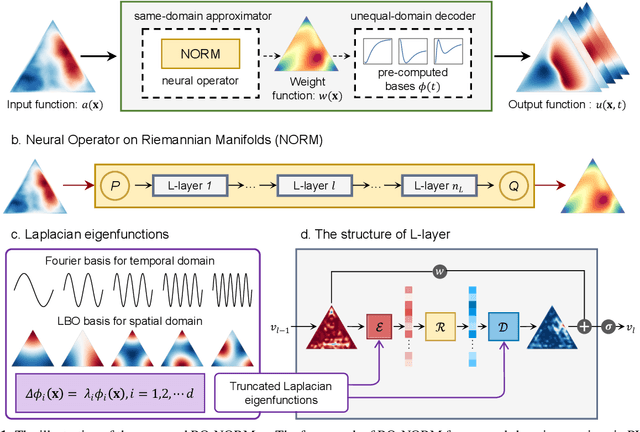
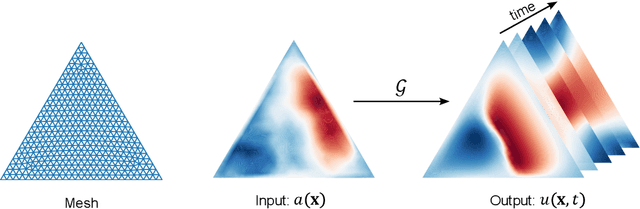
Predictive learning for spatio-temporal processes (PL-STP) on complex spatial domains plays a critical role in various scientific and engineering fields, with its essence being the construction of operators between infinite-dimensional function spaces. This paper focuses on the unequal-domain mappings in PL-STP and categorising them into increase-domain and decrease-domain mapping. Recent advances in deep learning have revealed the great potential of neural operators (NOs) to learn operators directly from observational data. However, existing NOs require input space and output space to be the same domain, which pose challenges in ensuring predictive accuracy and stability for unequal-domain mappings. To this end, this study presents a general reduced-order neural operator named Reduced-Order Neural Operator on Riemannian Manifolds (RO-NORM), which consists of two parts: the unequal-domain encoder/decoder and the same-domain approximator. Motivated by the variable separation in classical modal decomposition, the unequal-domain encoder/decoder uses the pre-computed bases to reformulate the spatio-temporal function as a sum of products between spatial (or temporal) bases and corresponding temporally (or spatially) distributed weight functions, thus the original unequal-domain mapping can be converted into a same-domain mapping. Consequently, the same-domain approximator NORM is applied to model the transformed mapping. The performance of our proposed method has been evaluated on six benchmark cases, including parametric PDEs, engineering and biomedical applications, and compared with four baseline algorithms: DeepONet, POD-DeepONet, PCA-Net, and vanilla NORM. The experimental results demonstrate the superiority of RO-NORM in prediction accuracy and training efficiency for PL-STP.

Residual fourier neural operator for thermochemical curing of composites

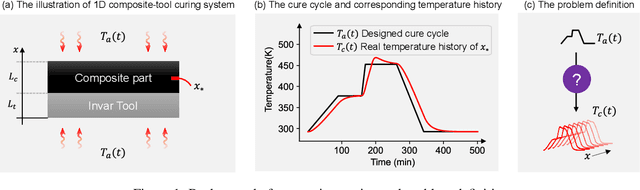
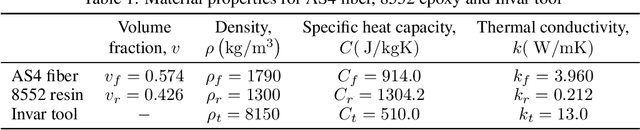
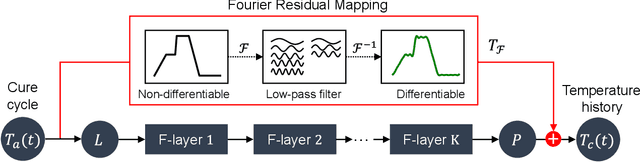
During the curing process of composites, the temperature history heavily determines the evolutions of the field of degree of cure as well as the residual stress, which will further influence the mechanical properties of composite, thus it is important to simulate the real temperature history to optimize the curing process of composites. Since thermochemical analysis using Finite Element (FE) simulations requires heavy computational loads and data-driven approaches suffer from the complexity of highdimensional mapping. This paper proposes a Residual Fourier Neural Operator (ResFNO) to establish the direct high-dimensional mapping from any given cure cycle to the corresponding temperature histories. By integrating domain knowledge into a time-resolution independent parameterized neural network, the mapping between cure cycles to temperature histories can be learned using limited number of labelled data. Besides, a novel Fourier residual mapping is designed based on mode decomposition to accelerate the training and boost the performance significantly. Several cases are carried out to evaluate the superior performance and generalizability of the proposed method comprehensively.