Training-Free Self-Correction for Multimodal Masked Diffusion Models

Masked diffusion models have emerged as a powerful framework for text and multimodal generation. However, their sampling procedure updates multiple tokens simultaneously and treats generated tokens as immutable, which may lead to error accumulation when early mistakes cannot be revised. In this work, we revisit existing self-correction methods and identify limitations stemming from additional training requirements or reliance on misaligned likelihood estimates. We propose a training-free self-correction framework that exploits the inductive biases of pre-trained masked diffusion models. Without modifying model parameters or introducing auxiliary evaluators, our method significantly improves generation quality on text-to-image generation and multimodal understanding tasks with reduced sampling steps. Moreover, the proposed framework generalizes across different masked diffusion architectures, highlighting its robustness and practical applicability. Code can be found in https://github.com/huge123/FreeCorrection.

Alignment of Diffusion Model and Flow Matching for Text-to-Image Generation

Diffusion models and flow matching have demonstrated remarkable success in text-to-image generation. While many existing alignment methods primarily focus on fine-tuning pre-trained generative models to maximize a given reward function, these approaches require extensive computational resources and may not generalize well across different objectives. In this work, we propose a novel alignment framework by leveraging the underlying nature of the alignment problem -- sampling from reward-weighted distributions -- and show that it applies to both diffusion models (via score guidance) and flow matching models (via velocity guidance). The score function (velocity field) required for the reward-weighted distribution can be decomposed into the pre-trained score (velocity field) plus a conditional expectation of the reward. For the alignment on the diffusion model, we identify a fundamental challenge: the adversarial nature of the guidance term can introduce undesirable artifacts in the generated images. Therefore, we propose a finetuning-free framework that trains a guidance network to estimate the conditional expectation of the reward. We achieve comparable performance to finetuning-based models with one-step generation with at least a 60% reduction in computational cost. For the alignment on flow matching, we propose a training-free framework that improves the generation quality without additional computational cost.

Corrected Samplers for Discrete Flow Models

Discrete flow models (DFMs) have been proposed to learn the data distribution on a finite state space, offering a flexible framework as an alternative to discrete diffusion models. A line of recent work has studied samplers for discrete diffusion models, such as tau-leaping and Euler solver. However, these samplers require a large number of iterations to control discretization error, since the transition rates are frozen in time and evaluated at the initial state within each time interval. Moreover, theoretical results for these samplers often require boundedness conditions of the transition rate or they focus on a specific type of source distributions. To address those limitations, we establish non-asymptotic discretization error bounds for those samplers without any restriction on transition rates and source distributions, under the framework of discrete flow models. Furthermore, by analyzing a one-step lower bound of the Euler sampler, we propose two corrected samplers: \textit{time-corrected sampler} and \textit{location-corrected sampler}, which can reduce the discretization error of tau-leaping and Euler solver with almost no additional computational cost. We rigorously show that the location-corrected sampler has a lower iteration complexity than existing parallel samplers. We validate the effectiveness of the proposed method by demonstrating improved generation quality and reduced inference time on both simulation and text-to-image generation tasks. Code can be found in https://github.com/WanZhengyan/Corrected-Samplers-for-Discrete-Flow-Models.

Error Analysis of Discrete Flow with Generator Matching

Discrete flow models offer a powerful framework for learning distributions over discrete state spaces and have demonstrated superior performance compared to the discrete diffusion model. However, their convergence properties and error analysis remain largely unexplored. In this work, we develop a unified framework grounded in stochastic calculus theory to systematically investigate the theoretical properties of discrete flow. Specifically, we derive the KL divergence of two path measures regarding two continuous-time Markov chains (CTMCs) with different transition rates by developing a novel Girsanov-type theorem, and provide a comprehensive analysis that encompasses the error arising from transition rate estimation and early stopping, where the first type of error has rarely been analyzed by existing works. Unlike discrete diffusion models, discrete flow incurs no truncation error caused by truncating the time horizon in the noising process. Building on generator matching and uniformization, we establish non-asymptotic error bounds for distribution estimation. Our results provide the first error analysis for discrete flow models.

Discrete Guidance Matching: Exact Guidance for Discrete Flow Matching

Guidance provides a simple and effective framework for posterior sampling by steering the generation process towards the desired distribution. When modeling discrete data, existing approaches mostly focus on guidance with the first-order Taylor approximation to improve the sampling efficiency. However, such an approximation is inappropriate in discrete state spaces since the approximation error could be large. A novel guidance framework for discrete data is proposed to address this problem: We derive the exact transition rate for the desired distribution given a learned discrete flow matching model, leading to guidance that only requires a single forward pass in each sampling step, significantly improving efficiency. This unified novel framework is general enough, encompassing existing guidance methods as special cases, and it can also be seamlessly applied to the masked diffusion model. We demonstrate the effectiveness of our proposed guidance on energy-guided simulations and preference alignment on text-to-image generation and multimodal understanding tasks. The code is available through https://github.com/WanZhengyan/Discrete-Guidance-Matching/tree/main.

Transfer Learning for Diffusion Models

Diffusion models, a specific type of generative model, have achieved unprecedented performance in recent years and consistently produce high-quality synthetic samples. A critical prerequisite for their notable success lies in the presence of a substantial number of training samples, which can be impractical in real-world applications due to high collection costs or associated risks. Consequently, various finetuning and regularization approaches have been proposed to transfer knowledge from existing pre-trained models to specific target domains with limited data. This paper introduces the Transfer Guided Diffusion Process (TGDP), a novel approach distinct from conventional finetuning and regularization methods. We prove that the optimal diffusion model for the target domain integrates pre-trained diffusion models on the source domain with additional guidance from a domain classifier. We further extend TGDP to a conditional version for modeling the joint distribution of data and its corresponding labels, together with two additional regularization terms to enhance the model performance. We validate the effectiveness of TGDP on Gaussian mixture simulations and on real electrocardiogram (ECG) datasets.

MissDiff: Training Diffusion Models on Tabular Data with Missing Values

The diffusion model has shown remarkable performance in modeling data distributions and synthesizing data. However, the vanilla diffusion model requires complete or fully observed data for training. Incomplete data is a common issue in various real-world applications, including healthcare and finance, particularly when dealing with tabular datasets. This work presents a unified and principled diffusion-based framework for learning from data with missing values under various missing mechanisms. We first observe that the widely adopted "impute-then-generate" pipeline may lead to a biased learning objective. Then we propose to mask the regression loss of Denoising Score Matching in the training phase. We prove the proposed method is consistent in learning the score of data distributions, and the proposed training objective serves as an upper bound for the negative likelihood in certain cases. The proposed framework is evaluated on multiple tabular datasets using realistic and efficacious metrics and is demonstrated to outperform state-of-the-art diffusion model on tabular data with "impute-then-generate" pipeline by a large margin.

Improving Adversarial Robustness by Contrastive Guided Diffusion Process

Synthetic data generation has become an emerging tool to help improve the adversarial robustness in classification tasks since robust learning requires a significantly larger amount of training samples compared with standard classification tasks. Among various deep generative models, the diffusion model has been shown to produce high-quality synthetic images and has achieved good performance in improving the adversarial robustness. However, diffusion-type methods are typically slow in data generation as compared with other generative models. Although different acceleration techniques have been proposed recently, it is also of great importance to study how to improve the sample efficiency of generated data for the downstream task. In this paper, we first analyze the optimality condition of synthetic distribution for achieving non-trivial robust accuracy. We show that enhancing the distinguishability among the generated data is critical for improving adversarial robustness. Thus, we propose the Contrastive-Guided Diffusion Process (Contrastive-DP), which adopts the contrastive loss to guide the diffusion model in data generation. We verify our theoretical results using simulations and demonstrate the good performance of Contrastive-DP on image datasets.

Attention Enables Zero Approximation Error

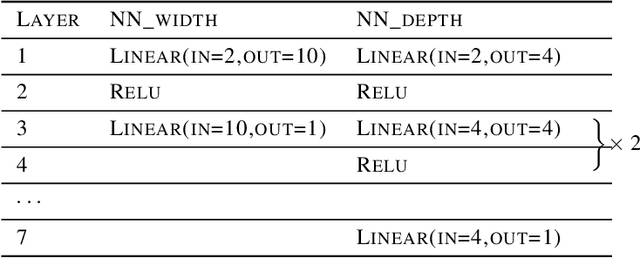
Deep learning models have been widely applied in various aspects of daily life. Many variant models based on deep learning structures have achieved even better performances. Attention-based architectures have become almost ubiquitous in deep learning structures. Especially, the transformer model has now defeated the convolutional neural network in image classification tasks to become the most widely used tool. However, the theoretical properties of attention-based models are seldom considered. In this work, we show that with suitable adaptations, the single-head self-attention transformer with a fixed number of transformer encoder blocks and free parameters is able to generate any desired polynomial of the input with no error. The number of transformer encoder blocks is the same as the degree of the target polynomial. Even more exciting, we find that these transformer encoder blocks in this model do not need to be trained. As a direct consequence, we show that the single-head self-attention transformer with increasing numbers of free parameters is universal. These surprising theoretical results clearly explain the outstanding performances of the transformer model and may shed light on future modifications in real applications. We also provide some experiments to verify our theoretical result.

Generalizing to Unseen Domains: A Survey on Domain Generalization

Domain generalization (DG), i.e., out-of-distribution generalization, has attracted increased interests in recent years. Domain generalization deals with a challenging setting where one or several different but related domain(s) are given, and the goal is to learn a model that can generalize to an unseen test domain. For years, great progress has been achieved. This paper presents the first review for recent advances in domain generalization. First, we provide a formal definition of domain generalization and discuss several related fields. Next, we thoroughly review the theories related to domain generalization and carefully analyze the theory behind generalization. Then, we categorize recent algorithms into three classes and present them in detail: data manipulation, representation learning, and learning strategy, each of which contains several popular algorithms. Third, we introduce the commonly used datasets and applications. Finally, we summarize existing literature and present some potential research topics for the future.