NeuroFly: A framework for whole-brain single neuron reconstruction

Neurons, with their elongated, tree-like dendritic and axonal structures, enable efficient signal integration and long-range communication across brain regions. By reconstructing individual neurons' morphology, we can gain valuable insights into brain connectivity, revealing the structure basis of cognition, movement, and perception. Despite the accumulation of extensive 3D microscopic imaging data, progress has been considerably hindered by the absence of automated tools to streamline this process. Here we introduce NeuroFly, a validated framework for large-scale automatic single neuron reconstruction. This framework breaks down the process into three distinct stages: segmentation, connection, and proofreading. In the segmentation stage, we perform automatic segmentation followed by skeletonization to generate over-segmented neuronal fragments without branches. During the connection stage, we use a 3D image-based path following approach to extend each fragment and connect it with other fragments of the same neuron. Finally, human annotators are required only to proofread the few unresolved positions. The first two stages of our process are clearly defined computer vision problems, and we have trained robust baseline models to solve them. We validated NeuroFly's efficiency using in-house datasets that include a variety of challenging scenarios, such as dense arborizations, weak axons, images with contamination. We will release the datasets along with a suite of visualization and annotation tools for better reproducibility. Our goal is to foster collaboration among researchers to address the neuron reconstruction challenge, ultimately accelerating advancements in neuroscience research. The dataset and code are available at https://github.com/beanli161514/neurofly

Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks

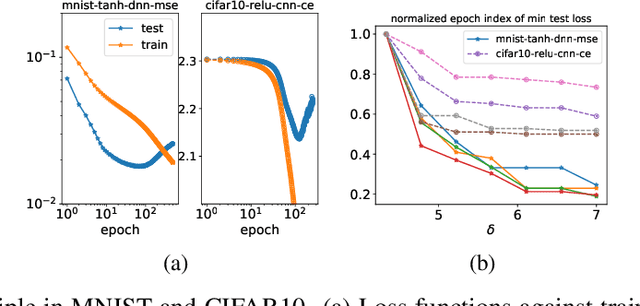
We study the training process of Deep Neural Networks (DNNs) from the Fourier analysis perspective. Our starting point is a Frequency Principle (F-Principle) --- DNNs initialized with small parameters often fit target functions from low to high frequencies --- which was first proposed by Xu et al. (2018) and Rahaman et al. (2018) on synthetic datasets. In this work, we first show the universality of the F-Principle by demonstrating this phenomenon on high-dimensional benchmark datasets, such as MNIST and CIFAR10. Then, based on experiments, we show that the F-Principle provides insight into both the success and failure of DNNs in different types of problems. Based on the F-Principle, we further propose that DNN can be adopted to accelerate the convergence of low frequencies for scientific computing problems, in which most of the conventional methods (e.g., Jacobi method) exhibit the opposite convergence behavior --- faster convergence for higher frequencies. Finally, we prove a theorem for DNNs of one hidden layer as a first step towards a mathematical explanation of the F-Principle. Our work indicates that the F-Principle with Fourier analysis is a promising approach to the study of DNNs because it seems ubiquitous, applicable, and explainable.

Training behavior of deep neural network in frequency domain

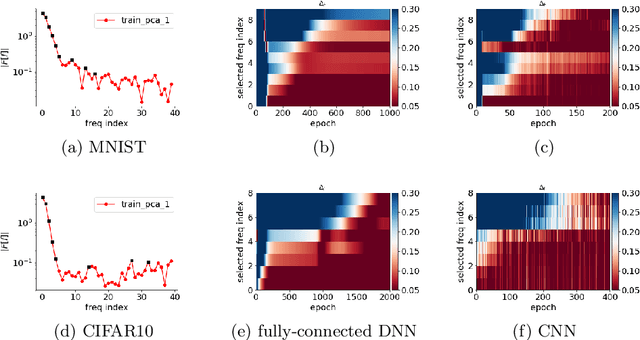
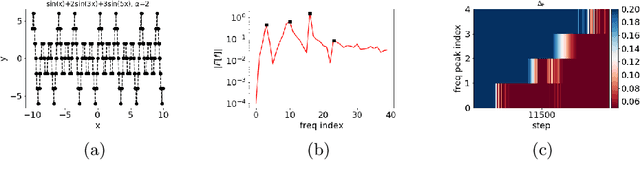
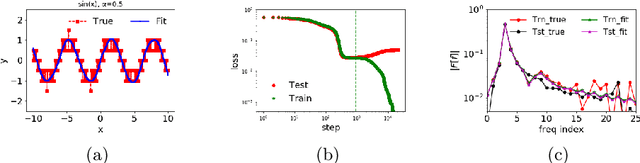
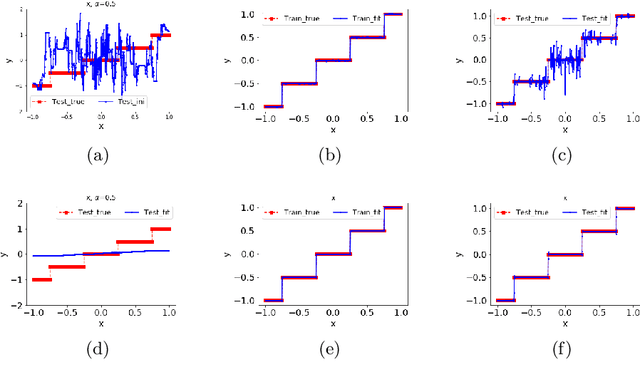
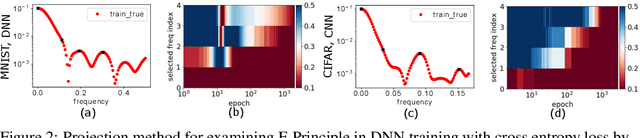
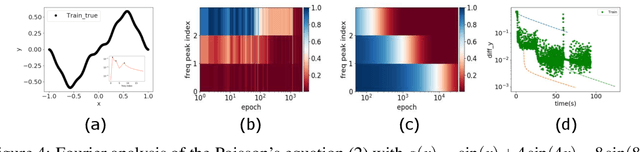
Why deep neural networks (DNNs) capable of overfitting often generalize well in practice is a mystery in deep learning. Existing works indicate that this observation holds for both complicated real datasets and simple datasets of one-dimensional (1-d) functions. In this work, for fitting low-frequency dominant 1-d functions, memorizing natural images and classification problems, we empirically found that a DNN, i.e., full-connected DNN or convolutional neural networks with common settings first quickly captures the dominant low-frequency components, and then relatively slowly captures high-frequency ones. We call this phenomenon Frequency Principle (F-Principle). F-Principle can be observed over various DNN setups of different activation functions, layer structures and training algorithms in our experiments. F-Principle can be used to understand (i) the behavior of DNN training in the information plane and (ii) why DNNs often generalize well albeit its ability of overfitting. This F-Principle potentially can provide insights into understanding the general principle underlying DNN optimization and generalization for real datasets.