Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks

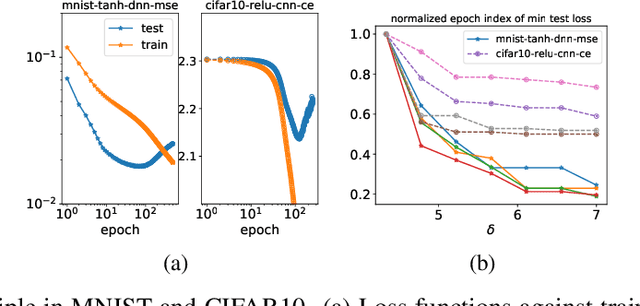
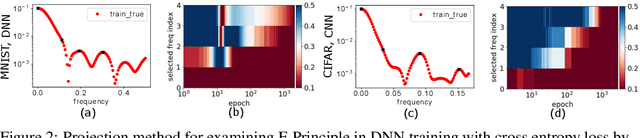
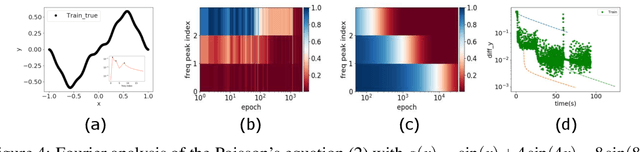
We study the training process of Deep Neural Networks (DNNs) from the Fourier analysis perspective. Our starting point is a Frequency Principle (F-Principle) --- DNNs initialized with small parameters often fit target functions from low to high frequencies --- which was first proposed by Xu et al. (2018) and Rahaman et al. (2018) on synthetic datasets. In this work, we first show the universality of the F-Principle by demonstrating this phenomenon on high-dimensional benchmark datasets, such as MNIST and CIFAR10. Then, based on experiments, we show that the F-Principle provides insight into both the success and failure of DNNs in different types of problems. Based on the F-Principle, we further propose that DNN can be adopted to accelerate the convergence of low frequencies for scientific computing problems, in which most of the conventional methods (e.g., Jacobi method) exhibit the opposite convergence behavior --- faster convergence for higher frequencies. Finally, we prove a theorem for DNNs of one hidden layer as a first step towards a mathematical explanation of the F-Principle. Our work indicates that the F-Principle with Fourier analysis is a promising approach to the study of DNNs because it seems ubiquitous, applicable, and explainable.