Training behavior of deep neural network in frequency domain

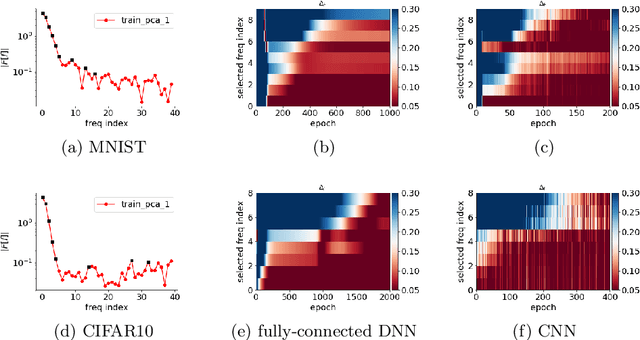
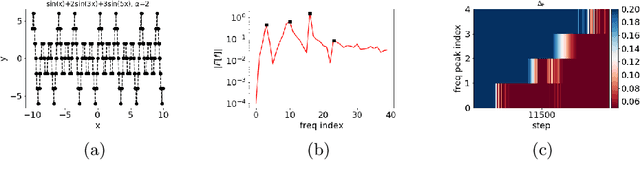
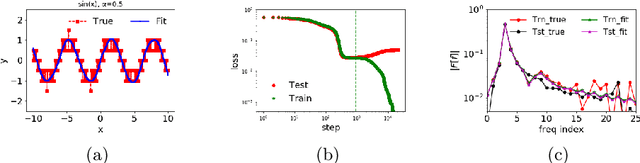
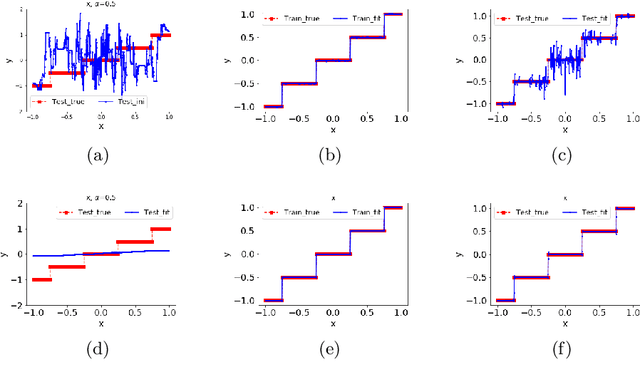
Why deep neural networks (DNNs) capable of overfitting often generalize well in practice is a mystery in deep learning. Existing works indicate that this observation holds for both complicated real datasets and simple datasets of one-dimensional (1-d) functions. In this work, for fitting low-frequency dominant 1-d functions, memorizing natural images and classification problems, we empirically found that a DNN, i.e., full-connected DNN or convolutional neural networks with common settings first quickly captures the dominant low-frequency components, and then relatively slowly captures high-frequency ones. We call this phenomenon Frequency Principle (F-Principle). F-Principle can be observed over various DNN setups of different activation functions, layer structures and training algorithms in our experiments. F-Principle can be used to understand (i) the behavior of DNN training in the information plane and (ii) why DNNs often generalize well albeit its ability of overfitting. This F-Principle potentially can provide insights into understanding the general principle underlying DNN optimization and generalization for real datasets.