Neural Decoding with Optimization of Node Activations

The problem of maximum likelihood decoding with a neural decoder for error-correcting code is considered. It is shown that the neural decoder can be improved with two novel loss terms on the node's activations. The first loss term imposes a sparse constraint on the node's activations. Whereas, the second loss term tried to mimic the node's activations from a teacher decoder which has better performance. The proposed method has the same run time complexity and model size as the neural Belief Propagation decoder, while improving the decoding performance by up to $1.1dB$ on BCH codes.

perm2vec: Graph Permutation Selection for Decoding of Error Correction Codes using Self-Attention

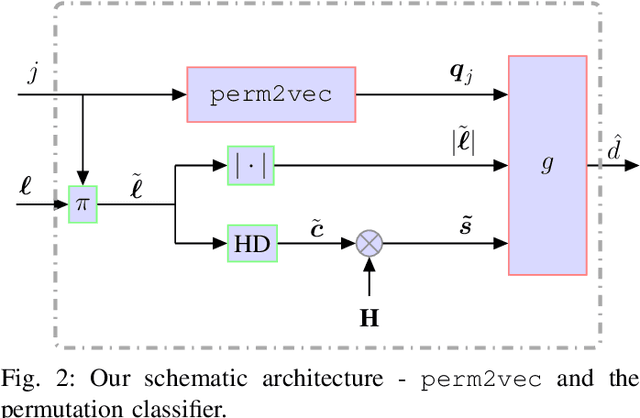
Error correction codes are integral part of communication applications, boosting the reliability of transmission. The optimal decoding of transmitted codewords is the maximum likelihood rule, which is NP-hard due to the curse of dimensionality. For practical realizations, suboptimal decoding algorithms are employed; yet limited theoretical insights prevents one from exploiting the full potential of these algorithms. One such insight is the choice of permutation in permutation decoding. We present a data-driven framework for permutation selection, combining domain knowledge with machine learning concepts such as node embedding and self-attention. Significant and consistent improvements in the bit error rate are introduced for all simulated codes, over the baseline decoders. To the best of the authors' knowledge, this work is the first to leverage the benefits of the neural Transformer networks in physical layer communication systems.

Active Deep Decoding of Linear Codes

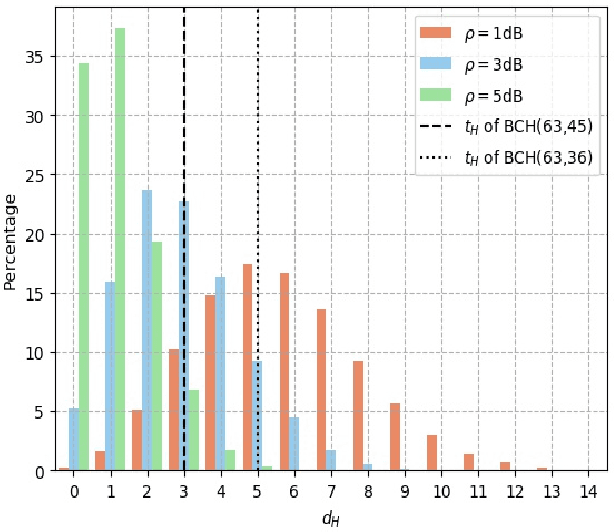
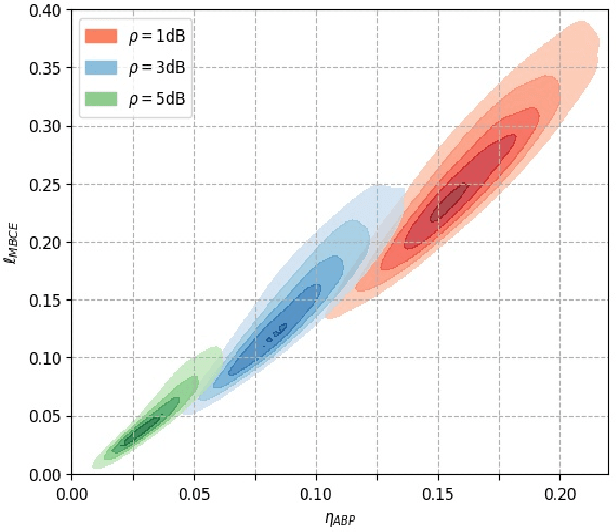
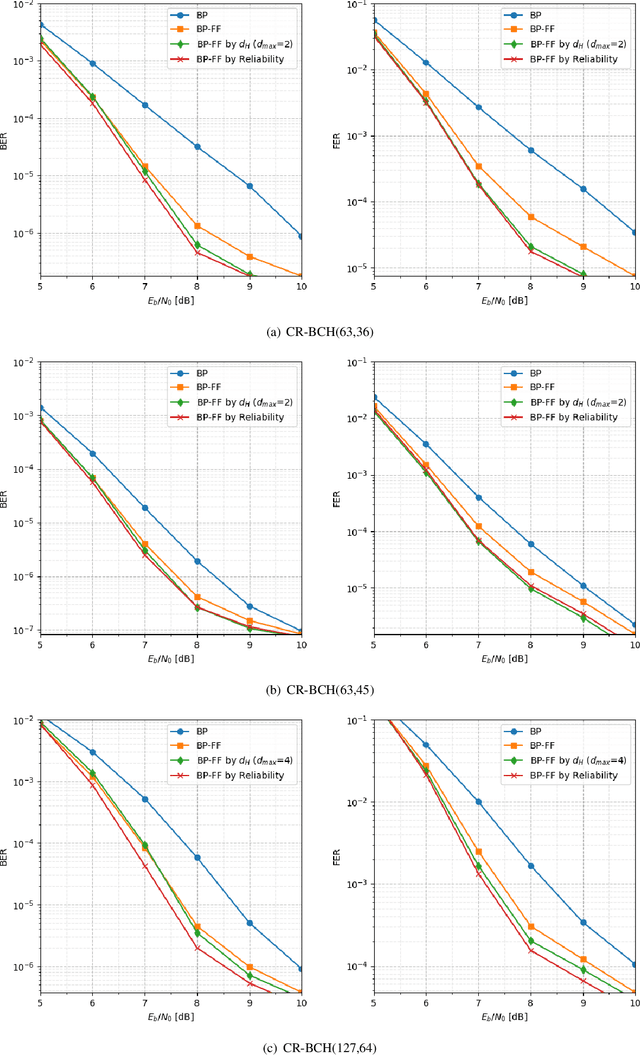
High quality data is essential in deep learning to train a robust model. While in other fields data is sparse and costly to collect, in error decoding it is free to query and label thus allowing potential data exploitation. Utilizing this fact and inspired by active learning, two novel methods are introduced to improve Weighted Belief Propagation (WBP) decoding. These methods incorporate machine-learning concepts with error decoding measures. For BCH(63,36), (63,45) and (127,64) codes, with cycle-reduced parity-check matrices, improvement of up to 1dB in BER and FER is demonstrated by smartly sampling the data, without increasing inference (decoding) complexity. The proposed methods constitutes an example guidelines for model enhancement by incorporation of domain knowledge from error-correcting field into a deep learning model. These guidelines can be adapted to any other deep learning based communication block.

Polar Decoding on Sparse Graphs with Deep Learning

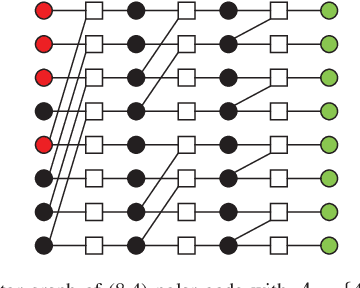
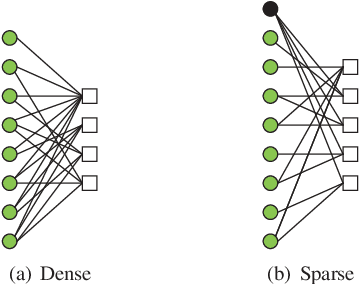
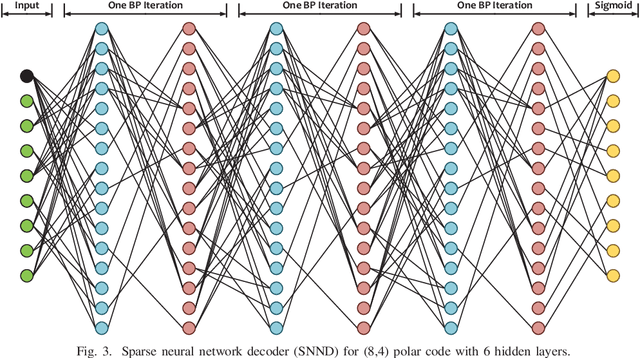
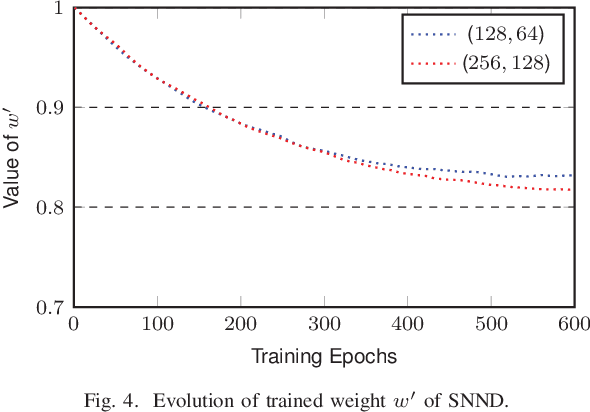
In this paper, we present a sparse neural network decoder (SNND) of polar codes based on belief propagation (BP) and deep learning. At first, the conventional factor graph of polar BP decoding is converted to the bipartite Tanner graph similar to low-density parity-check (LDPC) codes. Then the Tanner graph is unfolded and translated into the graphical representation of deep neural network (DNN). The complex sum-product algorithm (SPA) is modified to min-sum (MS) approximation with low complexity. We dramatically reduce the number of weight by using single weight to parameterize the networks. Optimized by the training techniques of deep learning, proposed SNND achieves comparative decoding performance of SPA and obtains about $0.5$ dB gain over MS decoding on ($128,64$) and ($256,128$) codes. Moreover, $60 \%$ complexity reduction is achieved and the decoding latency is significantly lower than the conventional polar BP.

Improving Massive MIMO Belief Propagation Detector with Deep Neural Network

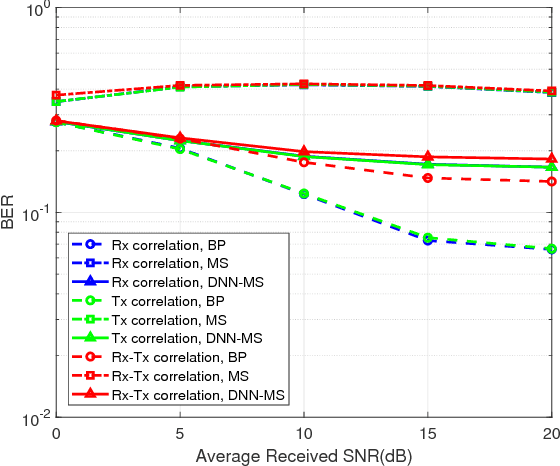
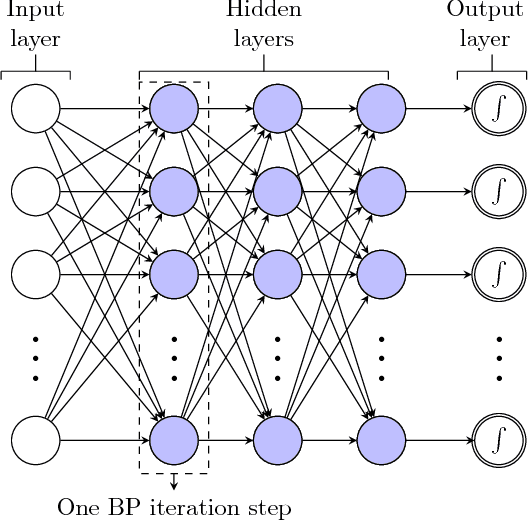
In this paper, deep neural network (DNN) is utilized to improve the belief propagation (BP) detection for massive multiple-input multiple-output (MIMO) systems. A neural network architecture suitable for detection task is firstly introduced by unfolding BP algorithms. DNN MIMO detectors are then proposed based on two modified BP detectors, damped BP and max-sum BP. The correction factors in these algorithms are optimized through deep learning techniques, aiming at improved detection performance. Numerical results are presented to demonstrate the performance of the DNN detectors in comparison with various BP modifications. The neural network is trained once and can be used for multiple online detections. The results show that, compared to other state-of-the-art detectors, the DNN detectors can achieve lower bit error rate (BER) with improved robustness against various antenna configurations and channel conditions at the same level of complexity.

Near Maximum Likelihood Decoding with Deep Learning

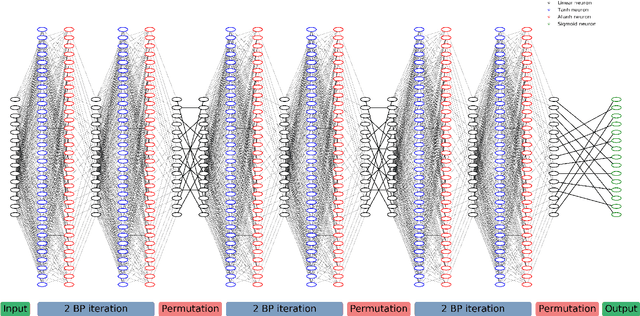
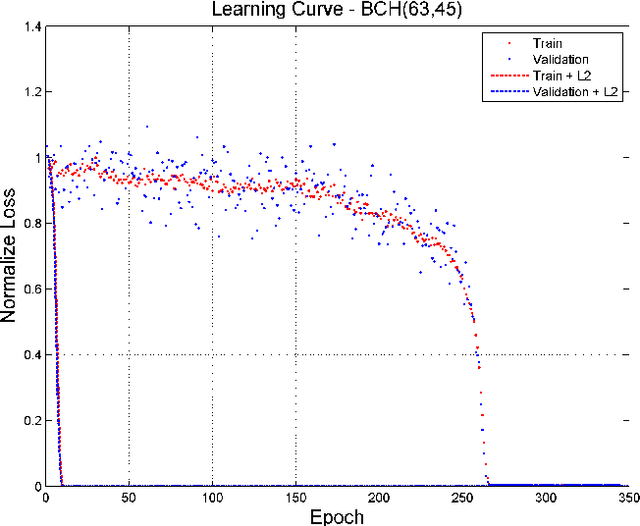
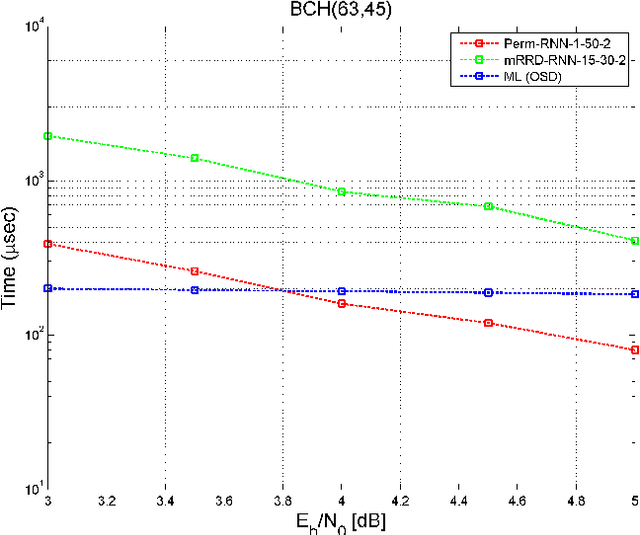
A novel and efficient neural decoder algorithm is proposed. The proposed decoder is based on the neural Belief Propagation algorithm and the Automorphism Group. By combining neural belief propagation with permutations from the Automorphism Group we achieve near maximum likelihood performance for High Density Parity Check codes. Moreover, the proposed decoder significantly improves the decoding complexity, compared to our earlier work on the topic. We also investigate the training process and show how it can be accelerated. Simulations of the hessian and the condition number show why the learning process is accelerated. We demonstrate the decoding algorithm for various linear block codes of length up to 63 bits.

RNN Decoding of Linear Block Codes

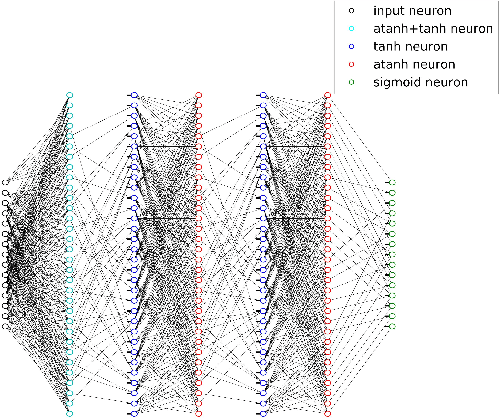
Designing a practical, low complexity, close to optimal, channel decoder for powerful algebraic codes with short to moderate block length is an open research problem. Recently it has been shown that a feed-forward neural network architecture can improve on standard belief propagation decoding, despite the large example space. In this paper we introduce a recurrent neural network architecture for decoding linear block codes. Our method shows comparable bit error rate results compared to the feed-forward neural network with significantly less parameters. We also demonstrate improved performance over belief propagation on sparser Tanner graph representations of the codes. Furthermore, we demonstrate that the RNN decoder can be used to improve the performance or alternatively reduce the computational complexity of the mRRD algorithm for low complexity, close to optimal, decoding of short BCH codes.