Near Maximum Likelihood Decoding with Deep Learning

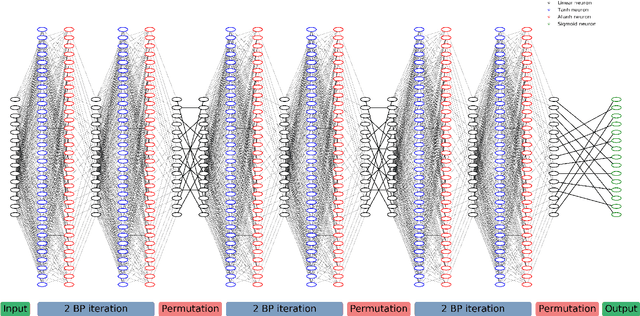
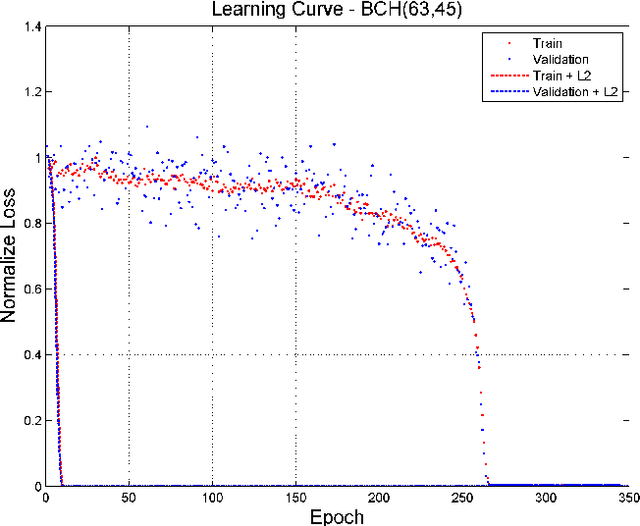
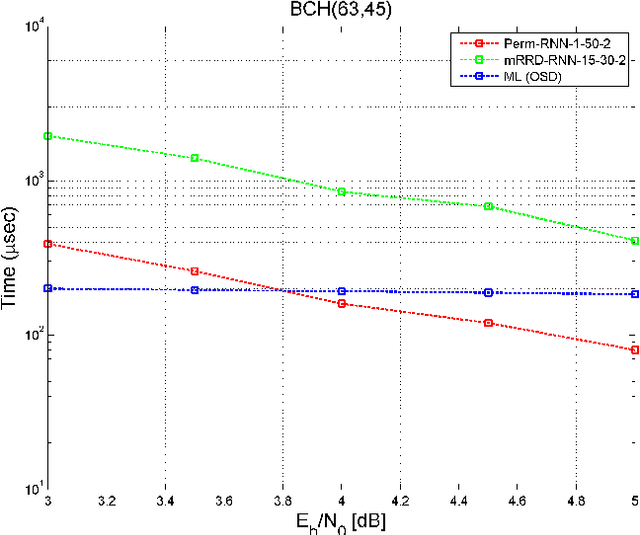
A novel and efficient neural decoder algorithm is proposed. The proposed decoder is based on the neural Belief Propagation algorithm and the Automorphism Group. By combining neural belief propagation with permutations from the Automorphism Group we achieve near maximum likelihood performance for High Density Parity Check codes. Moreover, the proposed decoder significantly improves the decoding complexity, compared to our earlier work on the topic. We also investigate the training process and show how it can be accelerated. Simulations of the hessian and the condition number show why the learning process is accelerated. We demonstrate the decoding algorithm for various linear block codes of length up to 63 bits.

Deep Learning Methods for Improved Decoding of Linear Codes

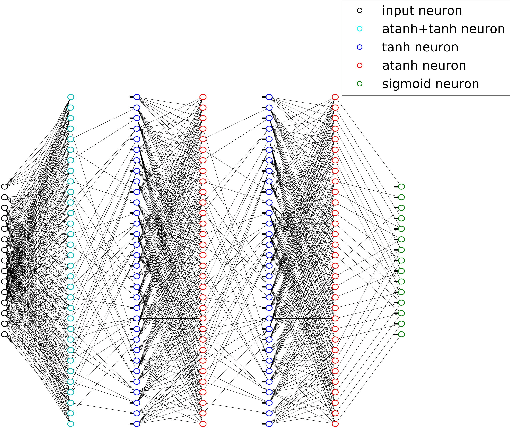
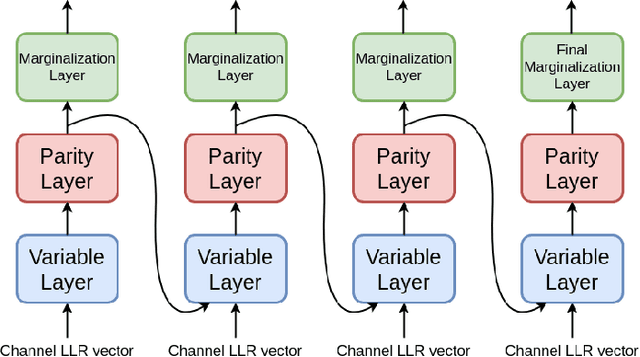
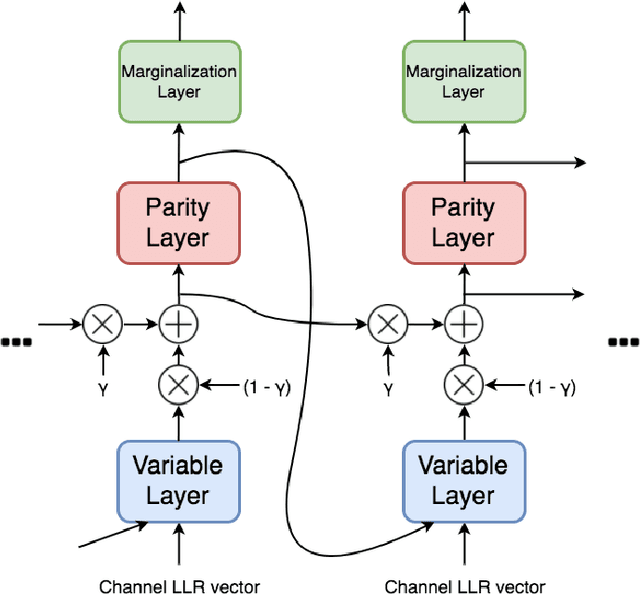
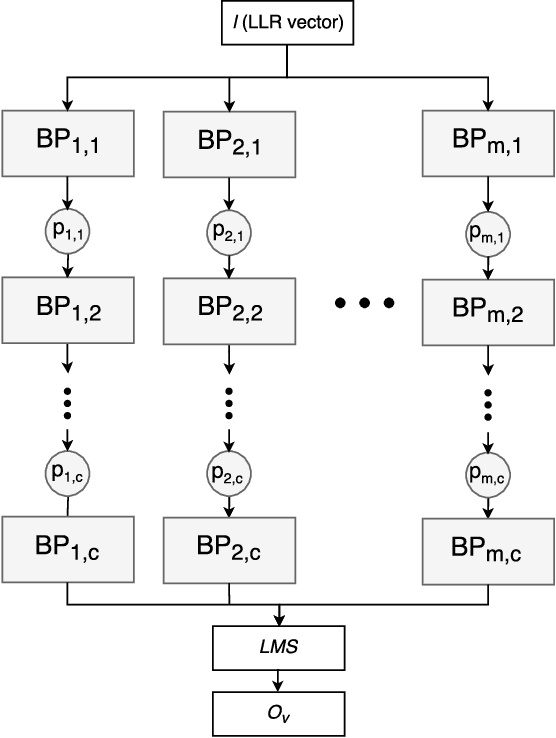
The problem of low complexity, close to optimal, channel decoding of linear codes with short to moderate block length is considered. It is shown that deep learning methods can be used to improve a standard belief propagation decoder, despite the large example space. Similar improvements are obtained for the min-sum algorithm. It is also shown that tying the parameters of the decoders across iterations, so as to form a recurrent neural network architecture, can be implemented with comparable results. The advantage is that significantly less parameters are required. We also introduce a recurrent neural decoder architecture based on the method of successive relaxation. Improvements over standard belief propagation are also observed on sparser Tanner graph representations of the codes. Furthermore, we demonstrate that the neural belief propagation decoder can be used to improve the performance, or alternatively reduce the computational complexity, of a close to optimal decoder of short BCH codes.

RNN Decoding of Linear Block Codes

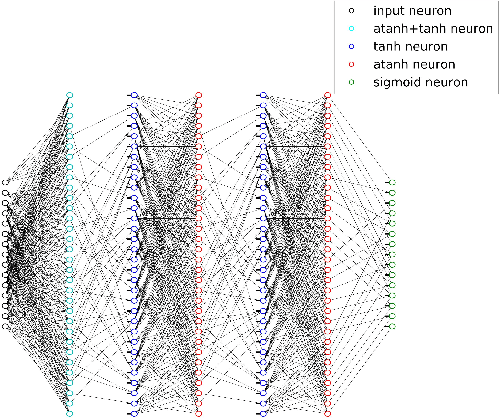
Designing a practical, low complexity, close to optimal, channel decoder for powerful algebraic codes with short to moderate block length is an open research problem. Recently it has been shown that a feed-forward neural network architecture can improve on standard belief propagation decoding, despite the large example space. In this paper we introduce a recurrent neural network architecture for decoding linear block codes. Our method shows comparable bit error rate results compared to the feed-forward neural network with significantly less parameters. We also demonstrate improved performance over belief propagation on sparser Tanner graph representations of the codes. Furthermore, we demonstrate that the RNN decoder can be used to improve the performance or alternatively reduce the computational complexity of the mRRD algorithm for low complexity, close to optimal, decoding of short BCH codes.