Deep Learning Methods for Improved Decoding of Linear Codes

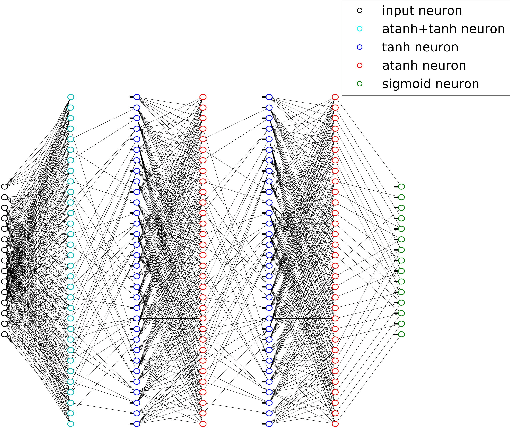
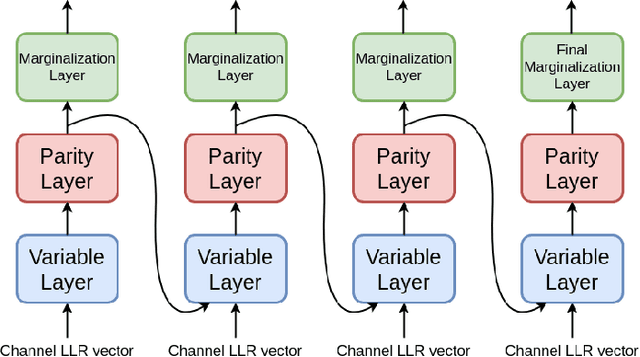
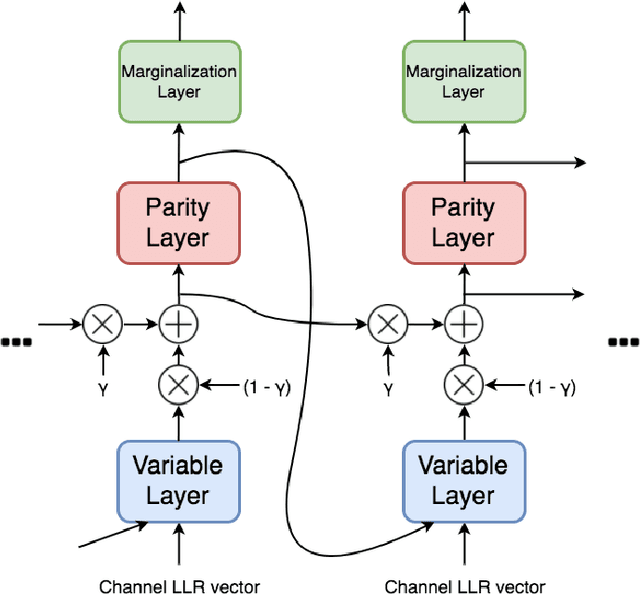
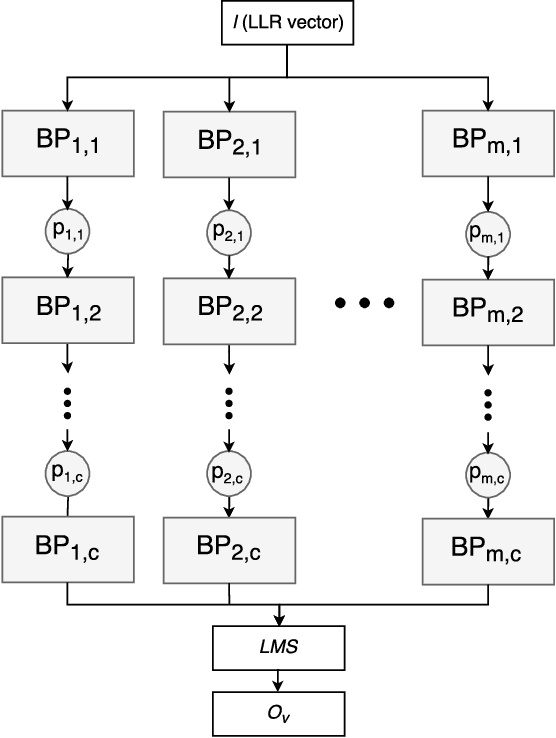
The problem of low complexity, close to optimal, channel decoding of linear codes with short to moderate block length is considered. It is shown that deep learning methods can be used to improve a standard belief propagation decoder, despite the large example space. Similar improvements are obtained for the min-sum algorithm. It is also shown that tying the parameters of the decoders across iterations, so as to form a recurrent neural network architecture, can be implemented with comparable results. The advantage is that significantly less parameters are required. We also introduce a recurrent neural decoder architecture based on the method of successive relaxation. Improvements over standard belief propagation are also observed on sparser Tanner graph representations of the codes. Furthermore, we demonstrate that the neural belief propagation decoder can be used to improve the performance, or alternatively reduce the computational complexity, of a close to optimal decoder of short BCH codes.

Learning to Decode Linear Codes Using Deep Learning

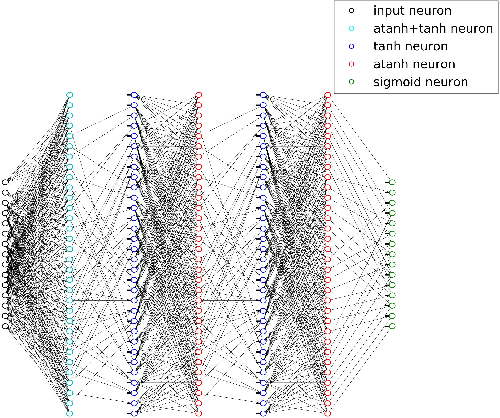
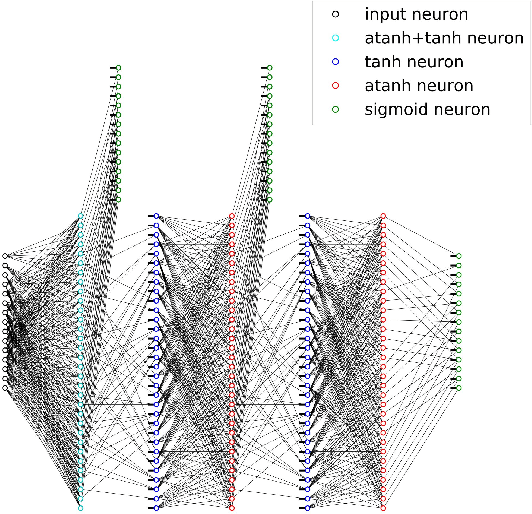
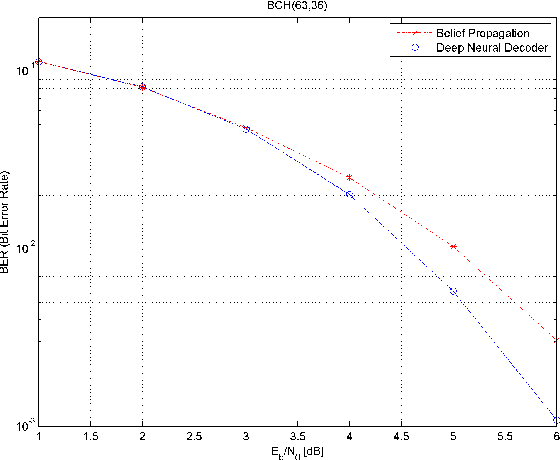
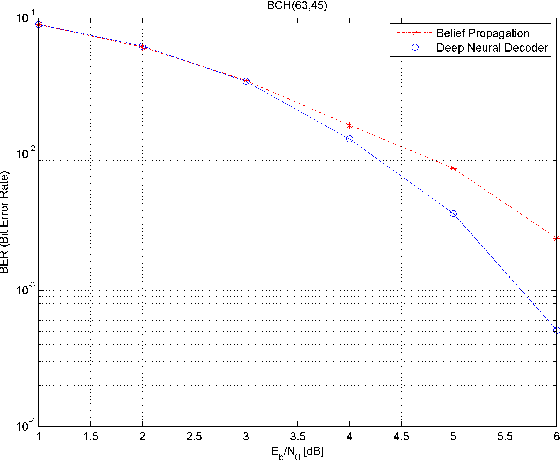
A novel deep learning method for improving the belief propagation algorithm is proposed. The method generalizes the standard belief propagation algorithm by assigning weights to the edges of the Tanner graph. These edges are then trained using deep learning techniques. A well-known property of the belief propagation algorithm is the independence of the performance on the transmitted codeword. A crucial property of our new method is that our decoder preserved this property. Furthermore, this property allows us to learn only a single codeword instead of exponential number of code-words. Improvements over the belief propagation algorithm are demonstrated for various high density parity check codes.