Polar Decoding on Sparse Graphs with Deep Learning
Paper and Code
Nov 24, 2018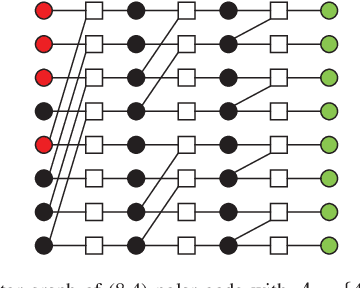
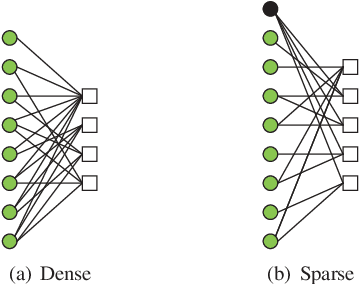
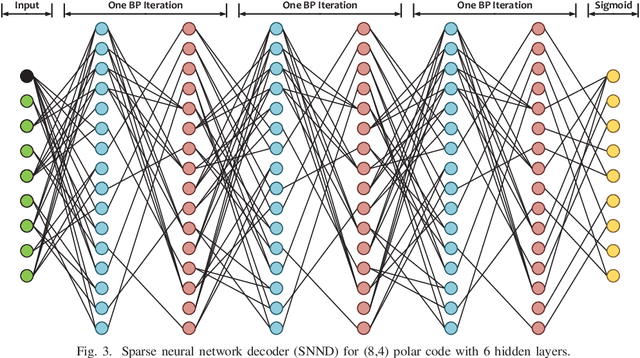
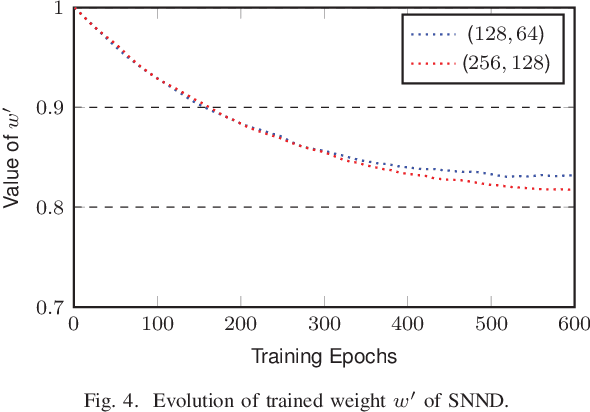
In this paper, we present a sparse neural network decoder (SNND) of polar codes based on belief propagation (BP) and deep learning. At first, the conventional factor graph of polar BP decoding is converted to the bipartite Tanner graph similar to low-density parity-check (LDPC) codes. Then the Tanner graph is unfolded and translated into the graphical representation of deep neural network (DNN). The complex sum-product algorithm (SPA) is modified to min-sum (MS) approximation with low complexity. We dramatically reduce the number of weight by using single weight to parameterize the networks. Optimized by the training techniques of deep learning, proposed SNND achieves comparative decoding performance of SPA and obtains about $0.5$ dB gain over MS decoding on ($128,64$) and ($256,128$) codes. Moreover, $60 \%$ complexity reduction is achieved and the decoding latency is significantly lower than the conventional polar BP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge