Algorithmic Fairness in Performative Policy Learning: Escaping the Impossibility of Group Fairness

In many prediction problems, the predictive model affects the distribution of the prediction target. This phenomenon is known as performativity and is often caused by the behavior of individuals with vested interests in the outcome of the predictive model. Although performativity is generally problematic because it manifests as distribution shifts, we develop algorithmic fairness practices that leverage performativity to achieve stronger group fairness guarantees in social classification problems (compared to what is achievable in non-performative settings). In particular, we leverage the policymaker's ability to steer the population to remedy inequities in the long term. A crucial benefit of this approach is that it is possible to resolve the incompatibilities between conflicting group fairness definitions.

A statistical framework for weak-to-strong generalization

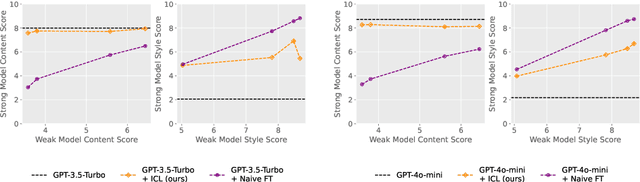
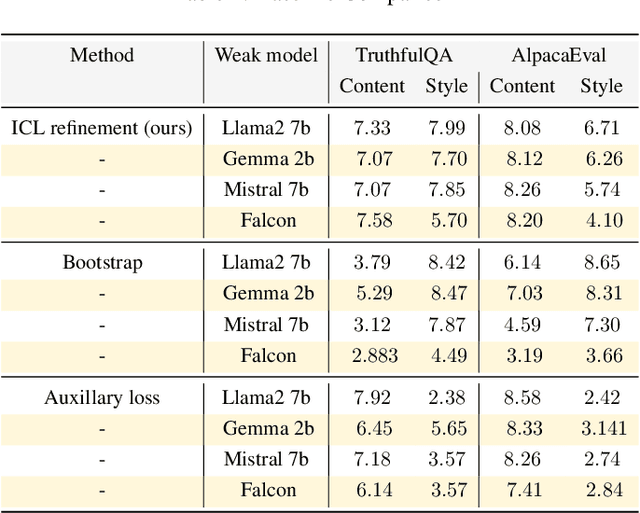
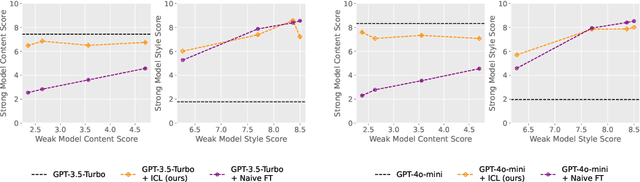
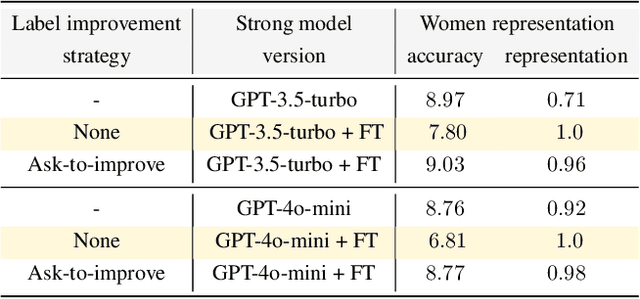
Modern large language model (LLM) alignment techniques rely on human feedback, but it is unclear whether the techniques fundamentally limit the capabilities of aligned LLMs. In particular, it is unclear whether it is possible to align (stronger) LLMs with superhuman capabilities with (weaker) human feedback without degrading their capabilities. This is an instance of the weak-to-strong generalization problem: using weaker (less capable) feedback to train a stronger (more capable) model. We prove that weak-to-strong generalization is possible by eliciting latent knowledge from pre-trained LLMs. In particular, we cast the weak-to-strong generalization problem as a transfer learning problem in which we wish to transfer a latent concept from a weak model to a strong pre-trained model. We prove that a naive fine-tuning approach suffers from fundamental limitations, but an alternative refinement-based approach suggested by the problem structure provably overcomes the limitations of fine-tuning. Finally, we demonstrate the practical applicability of the refinement approach with three LLM alignment tasks.

Learning In Reverse Causal Strategic Environments With Ramifications on Two Sided Markets

Motivated by equilibrium models of labor markets, we develop a formulation of causal strategic classification in which strategic agents can directly manipulate their outcomes. As an application, we compare employers that anticipate the strategic response of a labor force with employers that do not. We show through a combination of theory and experiment that employers with performatively optimal hiring policies improve employer reward, labor force skill level, and in some cases labor force equity. On the other hand, we demonstrate that performative employers harm labor force utility and fail to prevent discrimination in other cases.

Nonparametric Empirical Bayes Estimation and Testing for Sparse and Heteroscedastic Signals

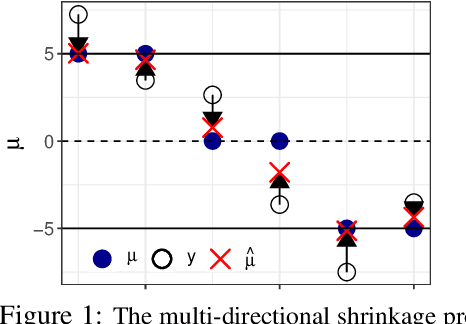
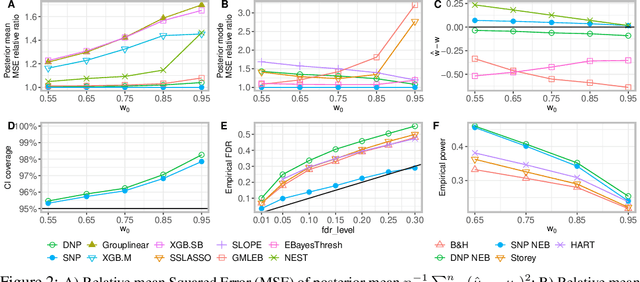
Large-scale modern data often involves estimation and testing for high-dimensional unknown parameters. It is desirable to identify the sparse signals, ``the needles in the haystack'', with accuracy and false discovery control. However, the unprecedented complexity and heterogeneity in modern data structure require new machine learning tools to effectively exploit commonalities and to robustly adjust for both sparsity and heterogeneity. In addition, estimates for high-dimensional parameters often lack uncertainty quantification. In this paper, we propose a novel Spike-and-Nonparametric mixture prior (SNP) -- a spike to promote the sparsity and a nonparametric structure to capture signals. In contrast to the state-of-the-art methods, the proposed methods solve the estimation and testing problem at once with several merits: 1) an accurate sparsity estimation; 2) point estimates with shrinkage/soft-thresholding property; 3) credible intervals for uncertainty quantification; 4) an optimal multiple testing procedure that controls false discovery rate. Our method exhibits promising empirical performance on both simulated data and a gene expression case study.

On conditional parity as a notion of non-discrimination in machine learning

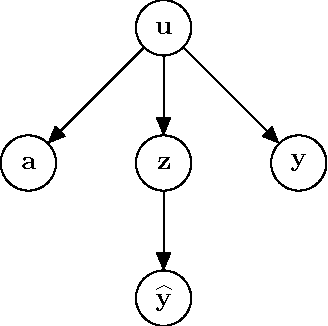
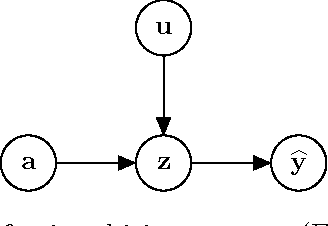
We identify conditional parity as a general notion of non-discrimination in machine learning. In fact, several recently proposed notions of non-discrimination, including a few counterfactual notions, are instances of conditional parity. We show that conditional parity is amenable to statistical analysis by studying randomization as a general mechanism for achieving conditional parity and a kernel-based test of conditional parity.

Sparse Empirical Bayes Analysis (SEBA)

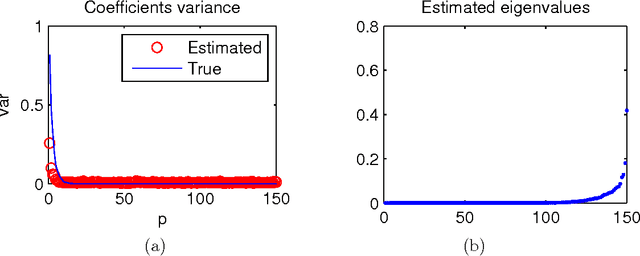
We consider a joint processing of $n$ independent sparse regression problems. Each is based on a sample $(y_{i1},x_{i1})...,(y_{im},x_{im})$ of $m$ \iid observations from $y_{i1}=x_{i1}\t\beta_i+\eps_{i1}$, $y_{i1}\in \R$, $x_{i 1}\in\R^p$, $i=1,...,n$, and $\eps_{i1}\dist N(0,\sig^2)$, say. $p$ is large enough so that the empirical risk minimizer is not consistent. We consider three possible extensions of the lasso estimator to deal with this problem, the lassoes, the group lasso and the RING lasso, each utilizing a different assumption how these problems are related. For each estimator we give a Bayesian interpretation, and we present both persistency analysis and non-asymptotic error bounds based on restricted eigenvalue - type assumptions.

LLE with low-dimensional neighborhood representation

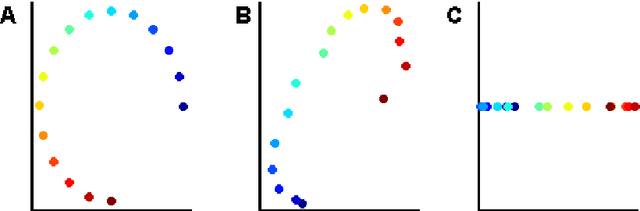
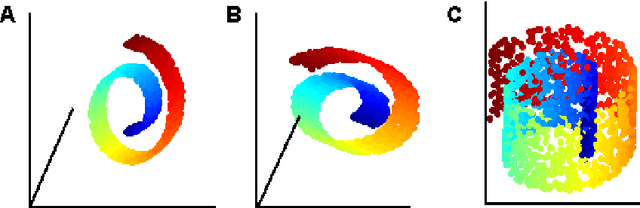
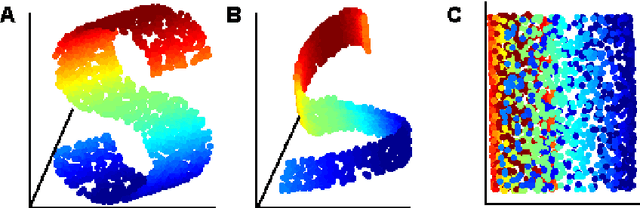
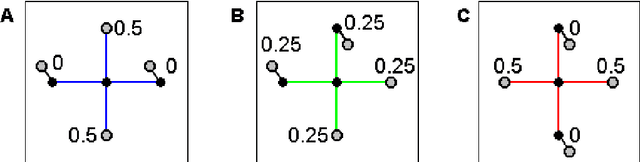
The local linear embedding algorithm (LLE) is a non-linear dimension-reducing technique, widely used due to its computational simplicity and intuitive approach. LLE first linearly reconstructs each input point from its nearest neighbors and then preserves these neighborhood relations in the low-dimensional embedding. We show that the reconstruction weights computed by LLE capture the high-dimensional structure of the neighborhoods, and not the low-dimensional manifold structure. Consequently, the weight vectors are highly sensitive to noise. Moreover, this causes LLE to converge to a linear projection of the input, as opposed to its non-linear embedding goal. To overcome both of these problems, we propose to compute the weight vectors using a low-dimensional neighborhood representation. We prove theoretically that this straightforward and computationally simple modification of LLE reduces LLE's sensitivity to noise. This modification also removes the need for regularization when the number of neighbors is larger than the dimension of the input. We present numerical examples demonstrating both the perturbation and linear projection problems, and the improved outputs using the low-dimensional neighborhood representation.