Silent Abandonment in Contact Centers: Estimating Customer Patience from Uncertain Data

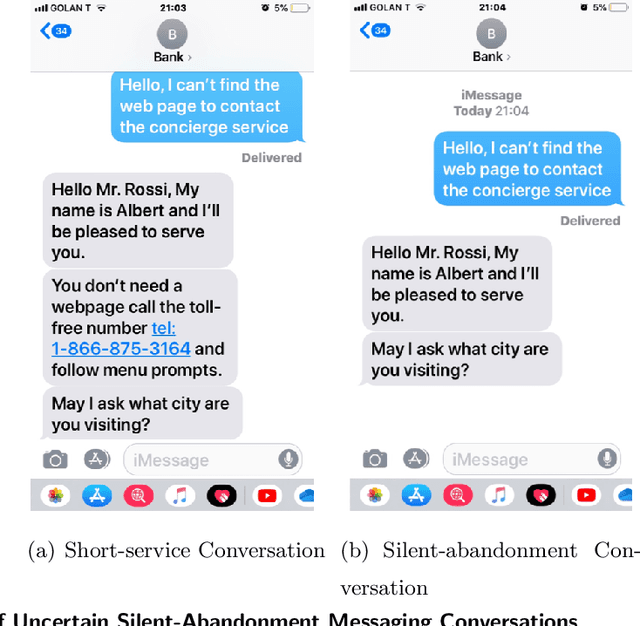
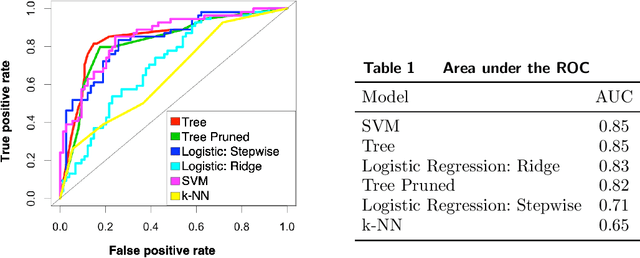
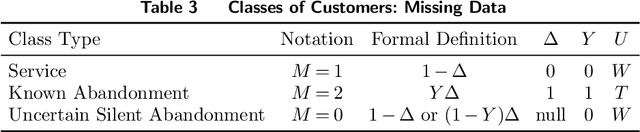
In the quest to improve services, companies offer customers the opportunity to interact with agents through contact centers, where the communication is mainly text-based. This has become one of the favorite channels of communication with companies in recent years. However, contact centers face operational challenges, since the measurement of common proxies for customer experience, such as knowledge of whether customers have abandoned the queue and their willingness to wait for service (patience), are subject to information uncertainty. We focus this research on the impact of a main source of such uncertainty: silent abandonment by customers. These customers leave the system while waiting for a reply to their inquiry, but give no indication of doing so, such as closing the mobile app of the interaction. As a result, the system is unaware that they have left and waste agent time and capacity until this fact is realized. In this paper, we show that 30%-67% of the abandoning customers abandon the system silently, and that such customer behavior reduces system efficiency by 5%-15%. To do so, we develop methodologies to identify silent-abandonment customers in two types of contact centers: chat and messaging systems. We first use text analysis and an SVM model to estimate the actual abandonment level. We then use a parametric estimator and develop an expectation-maximization algorithm to estimate customer patience accurately, as customer patience is an important parameter for fitting queueing models to the data. We show how accounting for silent abandonment in a queueing model improves dramatically the estimation accuracy of key measures of performance. Finally, we suggest strategies to operationally cope with the phenomenon of silent abandonment.

Kernel Machines With Missing Responses

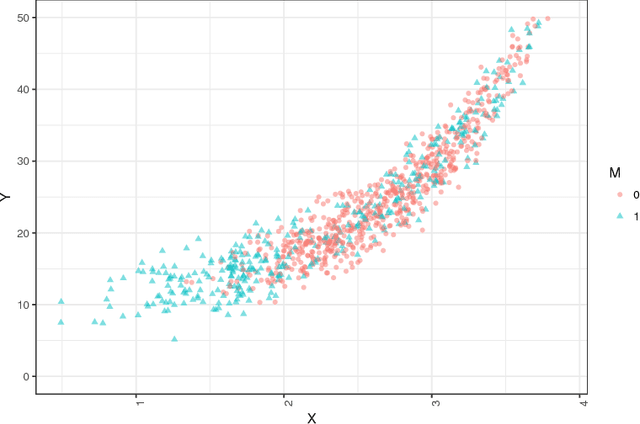
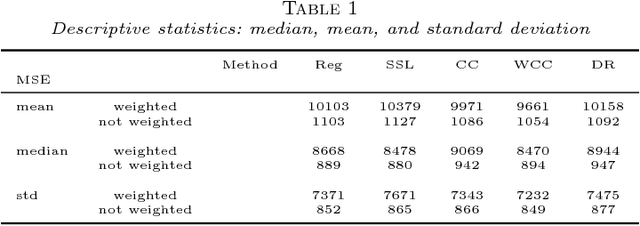
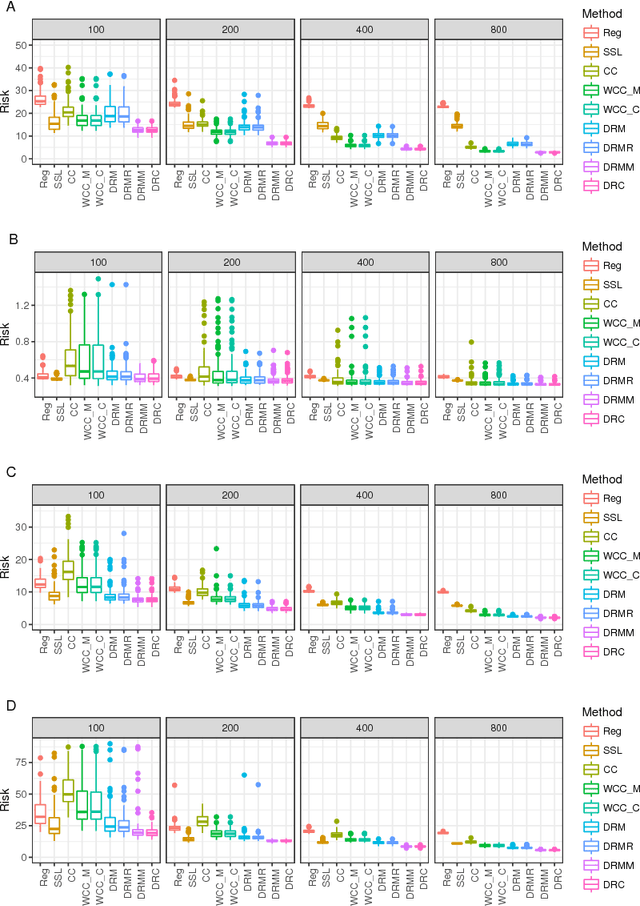
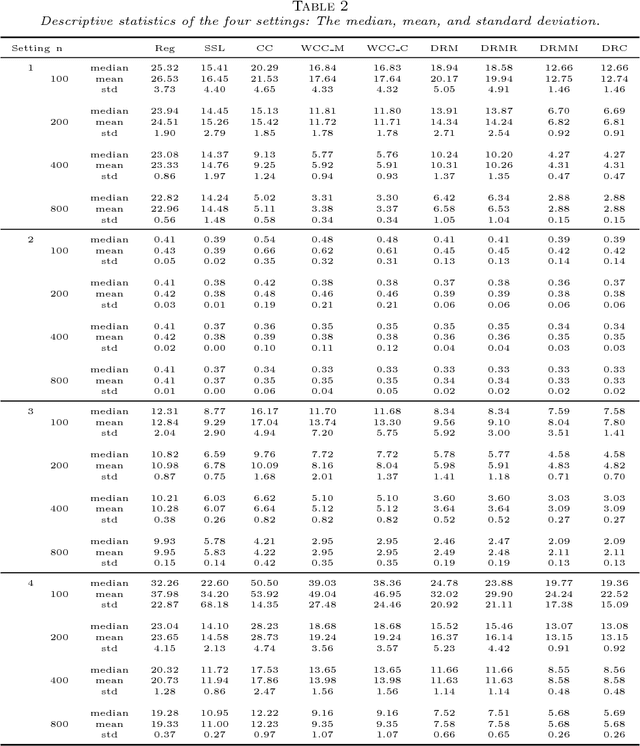
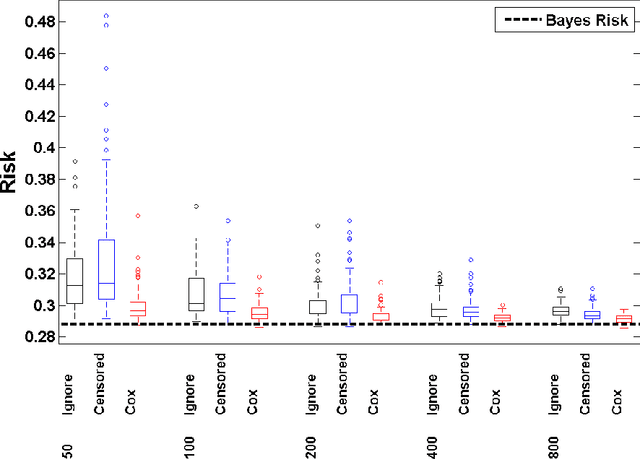
Missing responses is a missing data format in which outcomes are not always observed. In this work we develop kernel machines that can handle missing responses. First, we propose a kernel machine family that uses mainly the complete cases. For the quadratic loss, we then propose a family of doubly-robust kernel machines. The proposed kernel-machine estimators can be applied to both regression and classification problems. We prove oracle inequalities for the finite-sample differences between the kernel machine risk and Bayes risk. We use these oracle inequalities to prove consistency and to calculate convergence rates. We demonstrate the performance of the two proposed kernel machine families using both a simulation study and a real-world data analysis.

Feature Elimination in Kernel Machines in moderately high dimensions

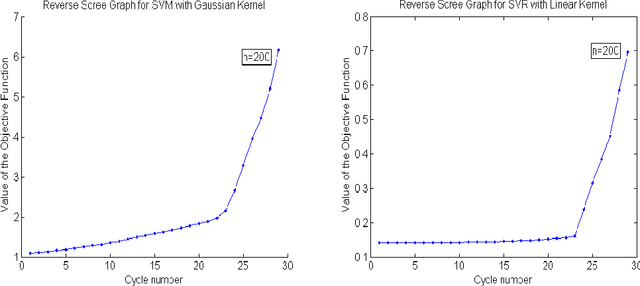
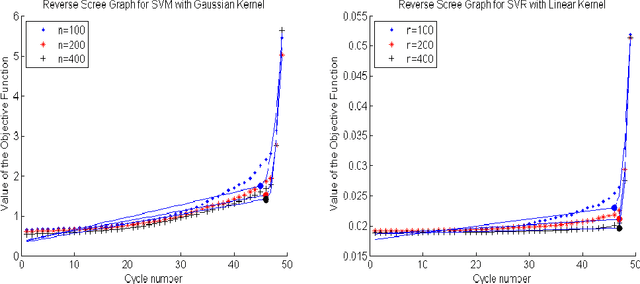
We develop an approach for feature elimination in statistical learning with kernel machines, based on recursive elimination of features.We present theoretical properties of this method and show that it is uniformly consistent in finding the correct feature space under certain generalized assumptions.We present four case studies to show that the assumptions are met in most practical situations and present simulation results to demonstrate performance of the proposed approach.

Support Vector Machines for Current Status Data

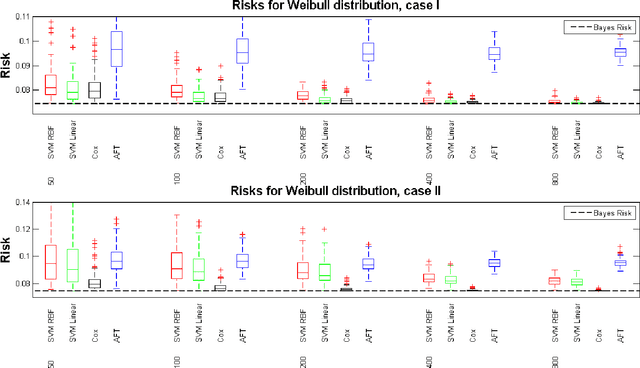
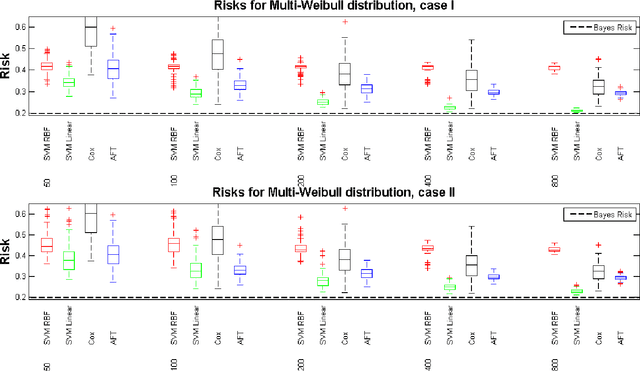
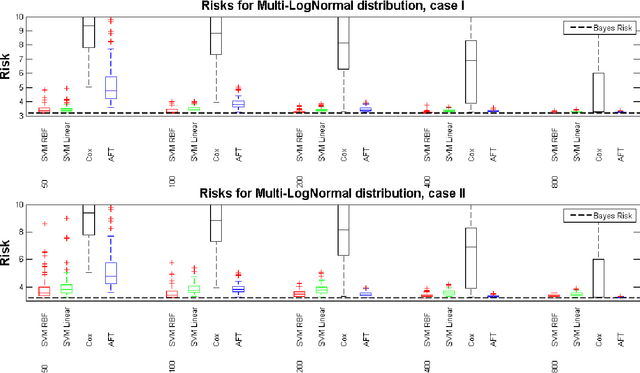
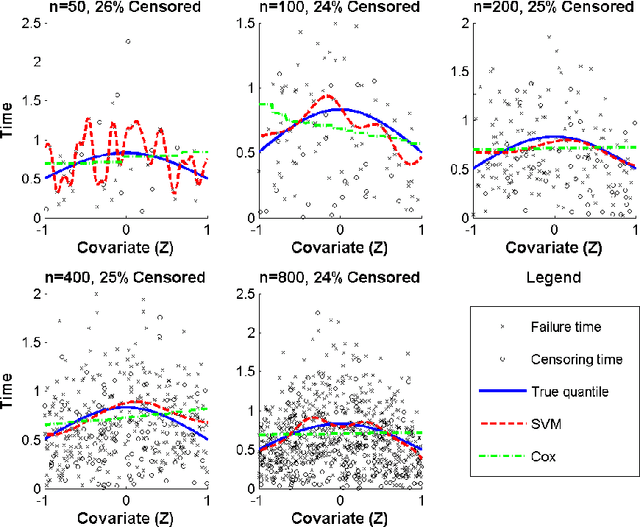
Current status data is a data format where the time to event is restricted to knowledge of whether or not the failure time exceeds a random monitoring time. We develop a support vector machine learning method for current status data that estimates the failure time expectation as a function of the covariates. In order to obtain the support vector machine decision function, we minimize a regularized version of the empirical risk with respect to a data-dependent loss. We show that the decision function has a closed form. Using finite sample bounds and novel oracle inequalities, we prove that the obtained decision function converges to the true conditional expectation for a large family of probability measures and study the associated learning rates. Finally we present a simulation study that compares the performance of the proposed approach to current state of the art.

Support Vector Regression for Right Censored Data

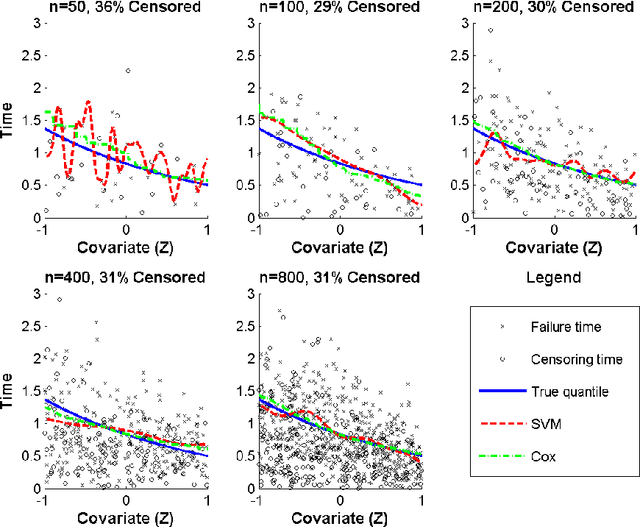
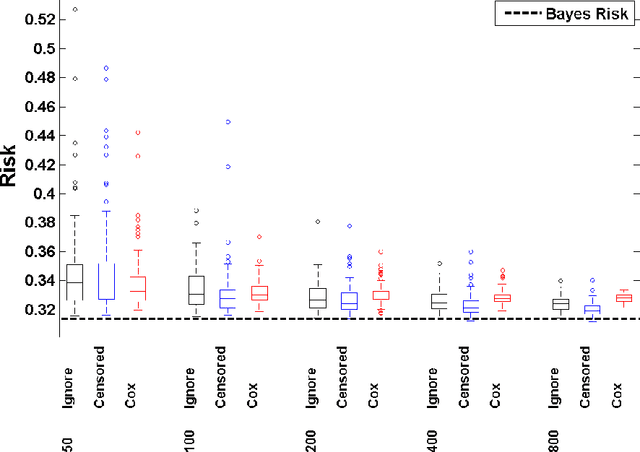
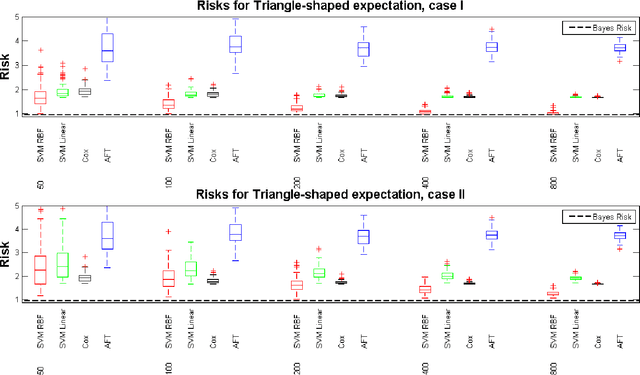
We develop a unified approach for classification and regression support vector machines for data subject to right censoring. We provide finite sample bounds on the generalization error of the algorithm, prove risk consistency for a wide class of probability measures, and study the associated learning rates. We apply the general methodology to estimation of the (truncated) mean, median, quantiles, and for classification problems. We present a simulation study that demonstrates the performance of the proposed approach.

LLE with low-dimensional neighborhood representation

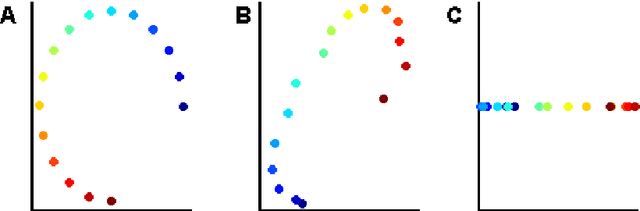
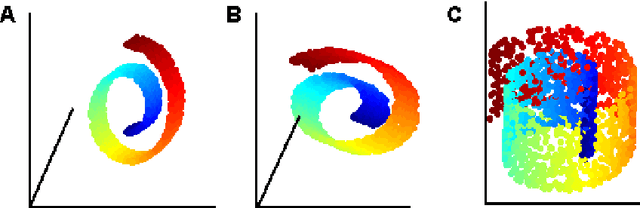
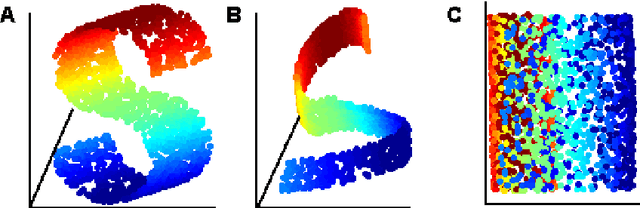
The local linear embedding algorithm (LLE) is a non-linear dimension-reducing technique, widely used due to its computational simplicity and intuitive approach. LLE first linearly reconstructs each input point from its nearest neighbors and then preserves these neighborhood relations in the low-dimensional embedding. We show that the reconstruction weights computed by LLE capture the high-dimensional structure of the neighborhoods, and not the low-dimensional manifold structure. Consequently, the weight vectors are highly sensitive to noise. Moreover, this causes LLE to converge to a linear projection of the input, as opposed to its non-linear embedding goal. To overcome both of these problems, we propose to compute the weight vectors using a low-dimensional neighborhood representation. We prove theoretically that this straightforward and computationally simple modification of LLE reduces LLE's sensitivity to noise. This modification also removes the need for regularization when the number of neighbors is larger than the dimension of the input. We present numerical examples demonstrating both the perturbation and linear projection problems, and the improved outputs using the low-dimensional neighborhood representation.