Shapley Marginal Surplus for Strong Models

Shapley values have seen widespread use in machine learning as a way to explain model predictions and estimate the importance of covariates. Accurately explaining models is critical in real-world models to both aid in decision making and to infer the properties of the true data-generating process (DGP). In this paper, we demonstrate that while model-based Shapley values might be accurate explainers of model predictions, machine learning models themselves are often poor explainers of the DGP even if the model is highly accurate. Particularly in the presence of interrelated or noisy variables, the output of a highly predictive model may fail to account for these relationships. This implies explanations of a trained model's behavior may fail to provide meaningful insight into the DGP. In this paper we introduce a novel variable importance algorithm, Shapley Marginal Surplus for Strong Models, that samples the space of possible models to come up with an inferential measure of feature importance. We compare this method to other popular feature importance methods, both Shapley-based and non-Shapley based, and demonstrate significant outperformance in inferential capabilities relative to other methods.

A Robust Hypothesis Test for Tree Ensemble Pruning

Gradient boosted decision trees are some of the most popular algorithms in applied machine learning. They are a flexible and powerful tool that can robustly fit to any tabular dataset in a scalable and computationally efficient way. One of the most critical parameters to tune when fitting these models are the various penalty terms used to distinguish signal from noise in the current model. These penalties are effective in practice, but are lacking in robust theoretical justifications. In this paper we develop and present a novel theoretically justified hypothesis test of split quality for gradient boosted tree ensembles and demonstrate that using this method instead of the common penalty terms leads to a significant reduction in out of sample loss. Additionally, this method provides a theoretically well-justified stopping condition for the tree growing algorithm. We also present several innovative extensions to the method, opening the door for a wide variety of novel tree pruning algorithms.

Feature Elimination in Kernel Machines in moderately high dimensions

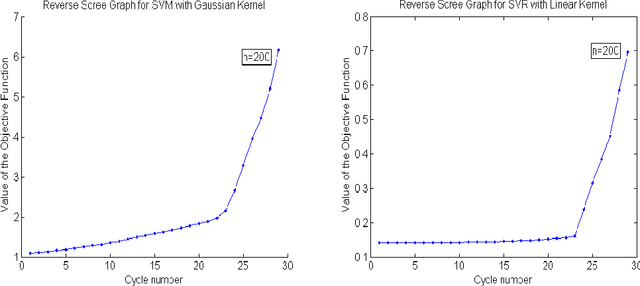
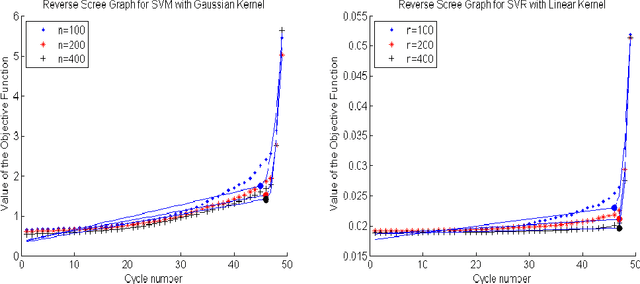
We develop an approach for feature elimination in statistical learning with kernel machines, based on recursive elimination of features.We present theoretical properties of this method and show that it is uniformly consistent in finding the correct feature space under certain generalized assumptions.We present four case studies to show that the assumptions are met in most practical situations and present simulation results to demonstrate performance of the proposed approach.