Natalia Bochkina
Sparse Empirical Bayes Analysis (SEBA)
Jan 08, 2010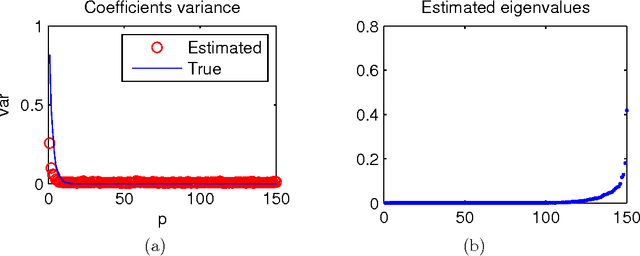
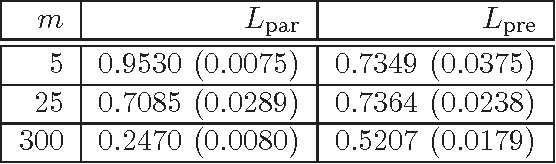
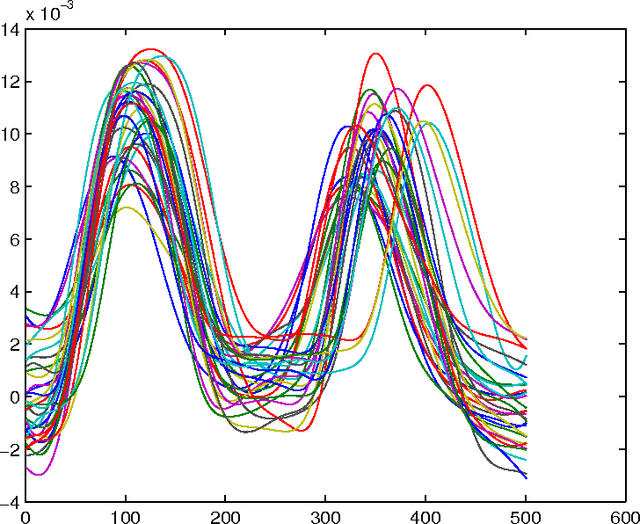

Abstract:We consider a joint processing of $n$ independent sparse regression problems. Each is based on a sample $(y_{i1},x_{i1})...,(y_{im},x_{im})$ of $m$ \iid observations from $y_{i1}=x_{i1}\t\beta_i+\eps_{i1}$, $y_{i1}\in \R$, $x_{i 1}\in\R^p$, $i=1,...,n$, and $\eps_{i1}\dist N(0,\sig^2)$, say. $p$ is large enough so that the empirical risk minimizer is not consistent. We consider three possible extensions of the lasso estimator to deal with this problem, the lassoes, the group lasso and the RING lasso, each utilizing a different assumption how these problems are related. For each estimator we give a Bayesian interpretation, and we present both persistency analysis and non-asymptotic error bounds based on restricted eigenvalue - type assumptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge