Inductive Matrix Completion and Root-MUSIC-Based Channel Estimation for Intelligent Reflecting Surface (IRS)-Aided Hybrid MIMO Systems

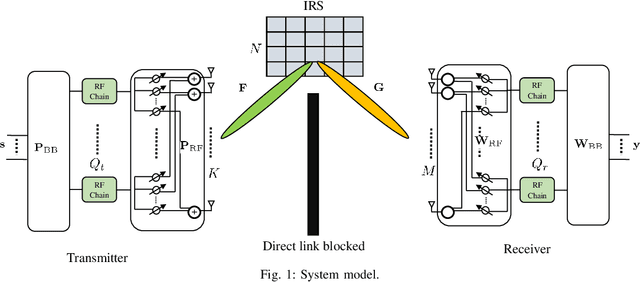
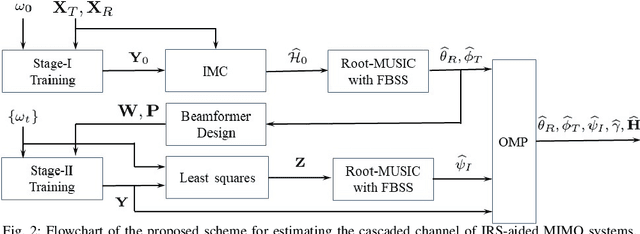
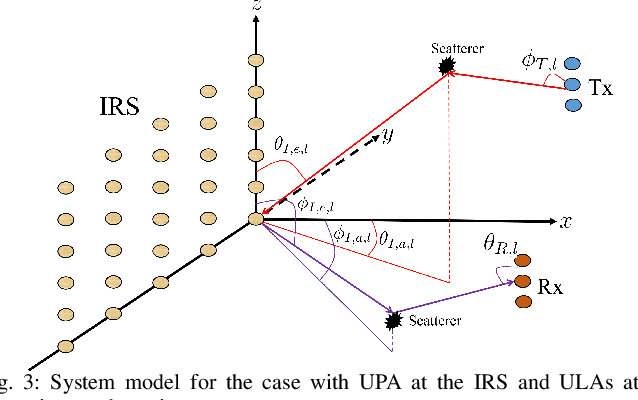
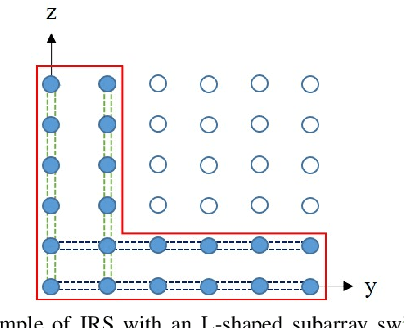
This paper studies the estimation of cascaded channels in passive intelligent reflective surface (IRS)- aided multiple-input multiple-output (MIMO) systems employing hybrid precoders and combiners. We propose a low-complexity solution that estimates the channel parameters progressively. The angles of departure (AoDs) and angles of arrival (AoAs) at the transmitter and receiver, respectively, are first estimated using inductive matrix completion (IMC) followed by root-MUSIC based super-resolution spectrum estimation. Forward-backward spatial smoothing (FBSS) is applied to address the coherence issue. Using the estimated AoAs and AoDs, the training precoders and combiners are then optimized and the angle differences between the AoAs and AoDs at the IRS are estimated using the least squares (LS) method followed by FBSS and the root-MUSIC algorithm. Finally, the composite path gains of the cascaded channel are estimated using on-grid sparse recovery with a small-size dictionary. The simulation results suggest that the proposed estimator can achieve improved channel parameter estimation performance with lower complexity as compared to several recently reported alternatives, thanks to the exploitation of the knowledge of the array responses and low-rankness of the channel using low-complexity algorithms at all the stages.

Study of Robust Sparsity-Aware RLS algorithms with Jointly-Optimized Parameters for Impulsive Noise Environments

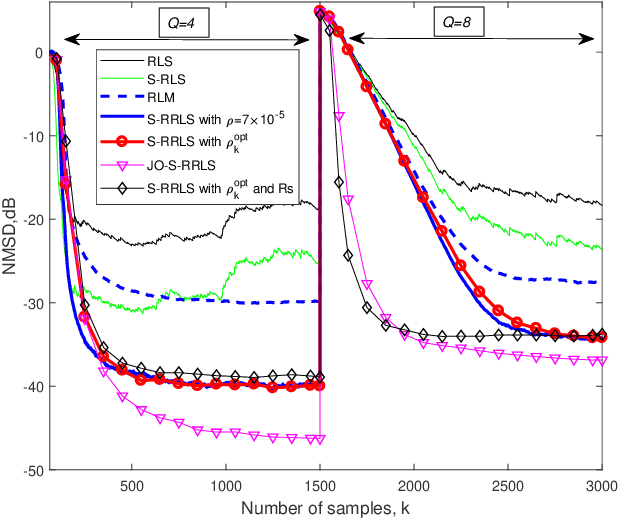
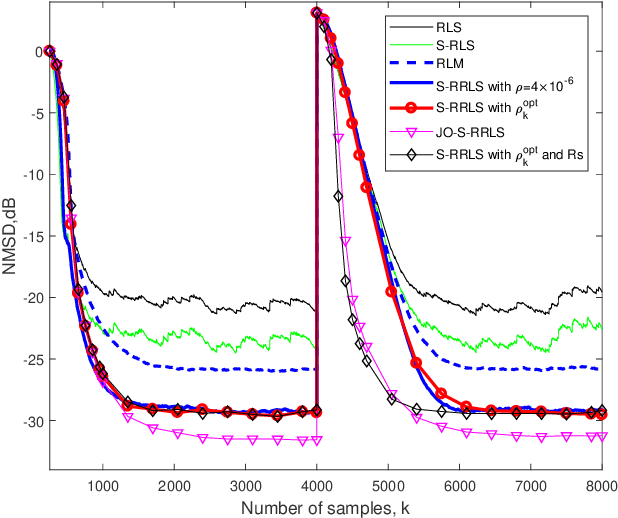
This paper proposes a unified sparsity-aware robust recursive least-squares RLS (S-RRLS) algorithm for the identification of sparse systems under impulsive noise. The proposed algorithm generalizes multiple algorithms only by replacing the specified criterion of robustness and sparsity-aware penalty. Furthermore, by jointly optimizing the forgetting factor and the sparsity penalty parameter, we develop the jointly-optimized S-RRLS (JO-S-RRLS) algorithm, which not only exhibits low misadjustment but also can track well sudden changes of a sparse system. Simulations in impulsive noise scenarios demonstrate that the proposed S-RRLS and JO-S-RRLS algorithms outperform existing techniques.

Study of filtered-x logarithmic recursive least $p$-power algorithm

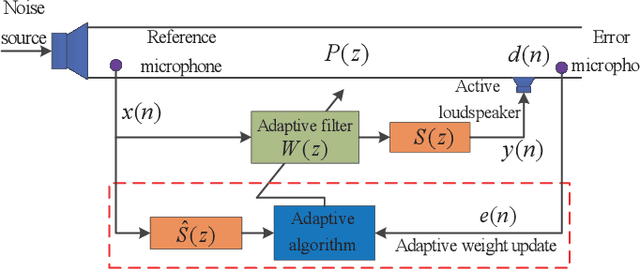
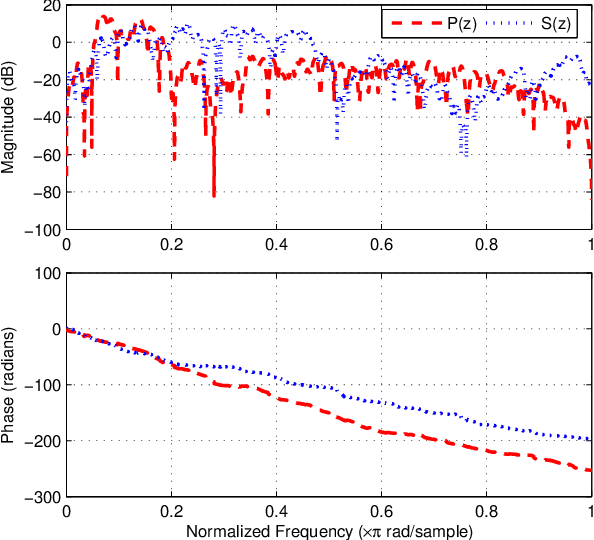
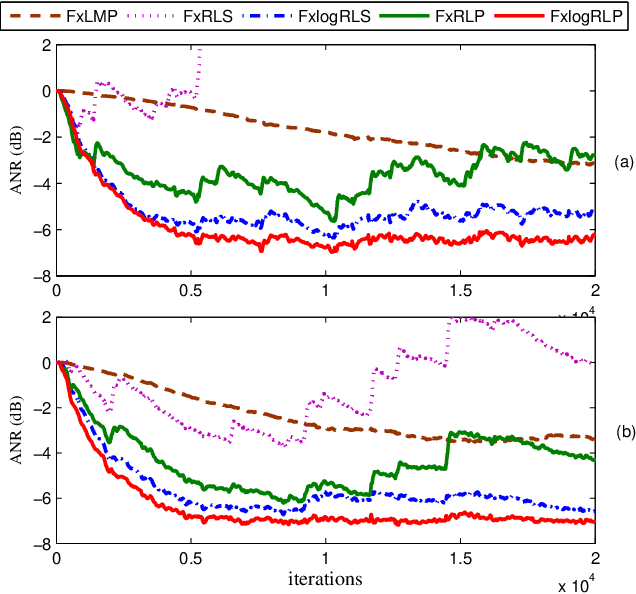
For active impulsive noise control, a filtered-x recursive least $p$-power (FxRLP) algorithm is proposed by minimizing the weighted summation of the $p$-power of the \emph{a posteriori} errors. Since the characteristic of the target noise is investigated, the FxRLP algorithm achieves good performance and robustness. To obtain a better performance, we develop a filtered-x logarithmic recursive least $p$-power (FxlogRLP) algorithm which integrates the $p$-order moment with the logarithmic-order moment. Simulation results demonstrate that the FxlogRLP algorithm is superior to the existing algorithms in terms of convergence rate and noise reduction.

Study of Frequency domain exponential functional link network filters

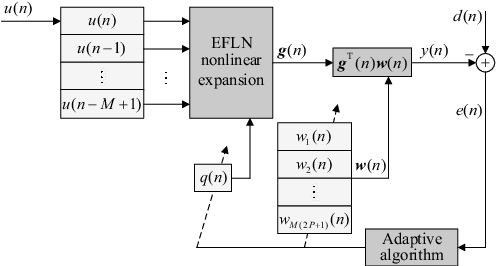
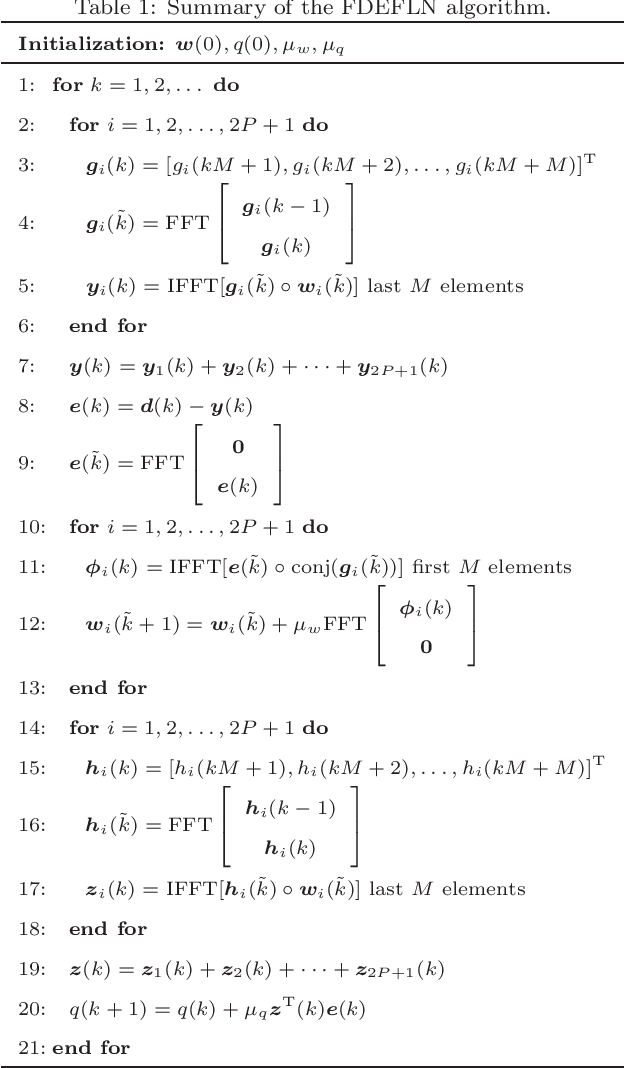
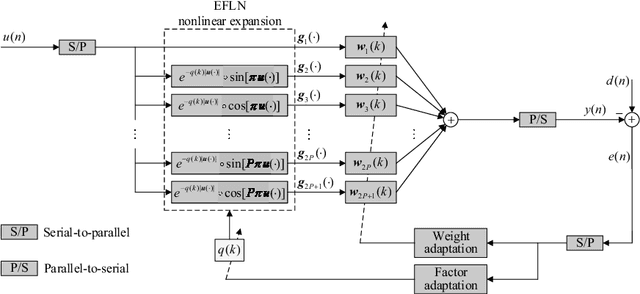
The exponential functional link network (EFLN) filter has attracted tremendous interest due to its enhanced nonlinear modeling capability. However, the computational complexity will dramatically increase with the dimension growth of the EFLN-based filter. To improve the computational efficiency, we propose a novel frequency domain exponential functional link network (FDEFLN) filter in this paper. The idea is to organize the samples in blocks of expanded input data, transform them from time domain to frequency domain, and thus execute the filtering and adaptation procedures in frequency domain with the overlap-save method. A FDEFLN-based nonlinear active noise control (NANC) system has also been developed to form the frequency domain exponential filtered-s least mean-square (FDEFsLMS) algorithm. Moreover, the stability, steady-state performance and computational complexity of algorithms are analyzed. Finally, several numerical experiments corroborate the proposed FDEFLN-based algorithms in nonlinear system identification, acoustic echo cancellation and NANC implementations, which demonstrate much better computational efficiency.

Robust Adaptive Filtering Based on Exponential Functional Link Network

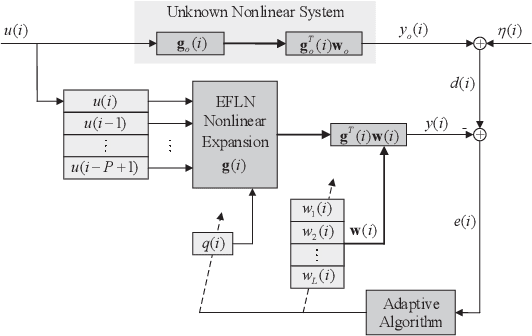
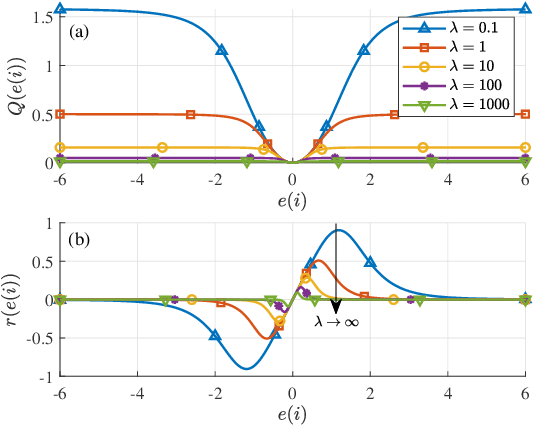
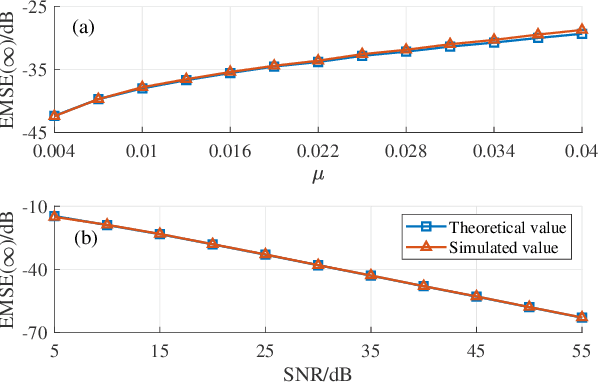
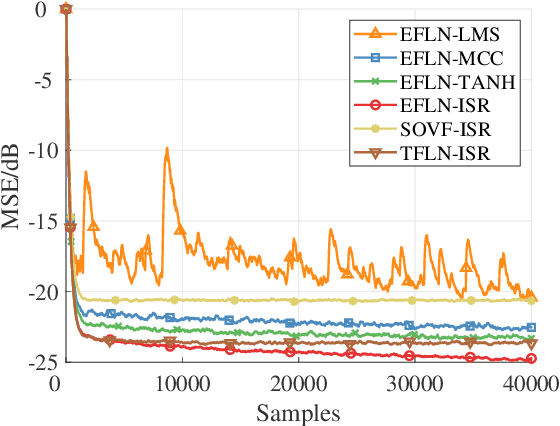
The exponential functional link network (EFLN) has been recently investigated and applied to nonlinear filtering. This brief proposes an adaptive EFLN filtering algorithm based on a novel inverse square root (ISR) cost function, called the EFLN-ISR algorithm, whose learning capability is robust under impulsive interference. The steady-state performance of EFLN-ISR is rigorously derived and then confirmed by numerical simulations. Moreover, the validity of the proposed EFLN-ISR algorithm is justified by the actually experimental results with the application to hysteretic nonlinear system identification.

Study of Diffusion Normalized Least Mean M-estimate Algorithms

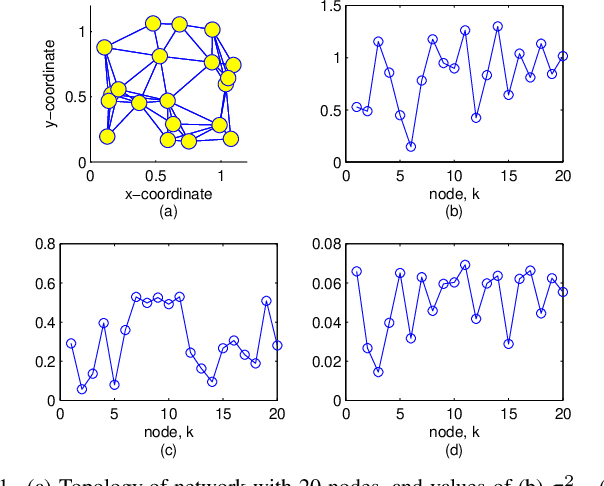
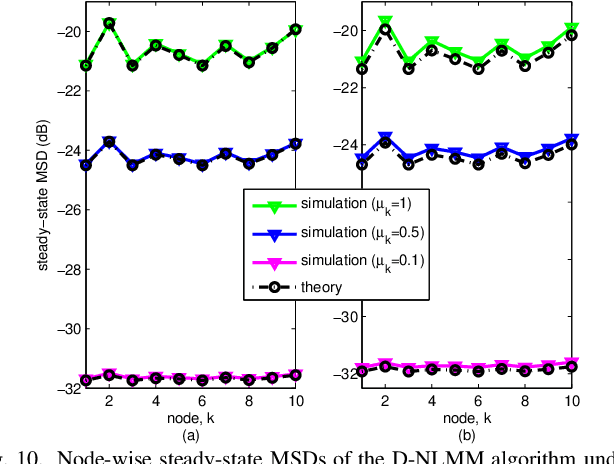
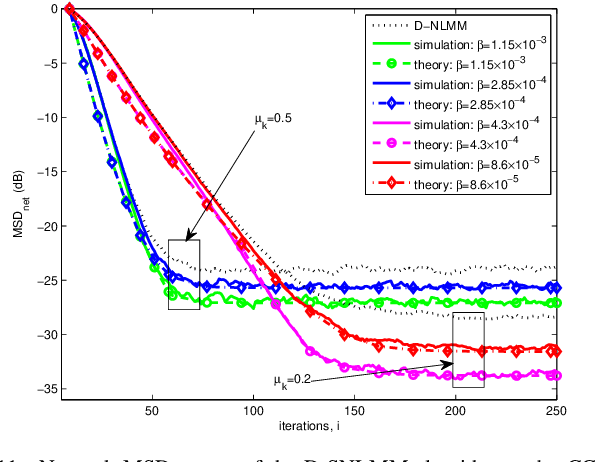
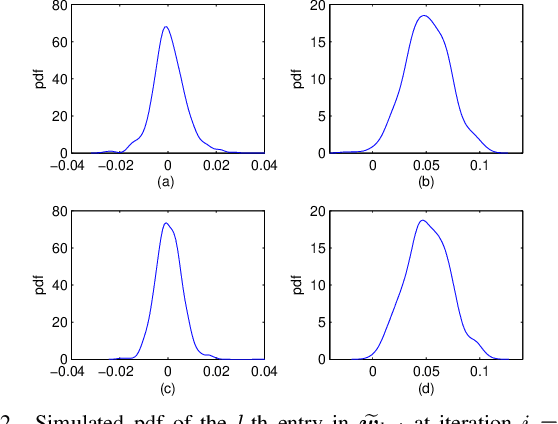
This work proposes diffusion normalized least mean M-estimate algorithm based on the modified Huber function, which can equip distributed networks with robust learning capability in the presence of impulsive interference. In order to exploit the system's underlying sparsity to further improve the learning performance, a sparse-aware variant is also developed by incorporating the $l_0$-norm of the estimates into the update process. We then analyze the transient, steady-state and stability behaviors of the algorithms in a unified framework. In particular, we present an analytical method that is simpler than conventional approaches to deal with the score function since it removes the requirements of integrals and Price's theorem. Simulations in various impulsive noise scenarios show that the proposed algorithms are superior to some existing diffusion algorithms and the theoretical results are verifiable.

Robust DCD-Based Recursive Adaptive Algorithms

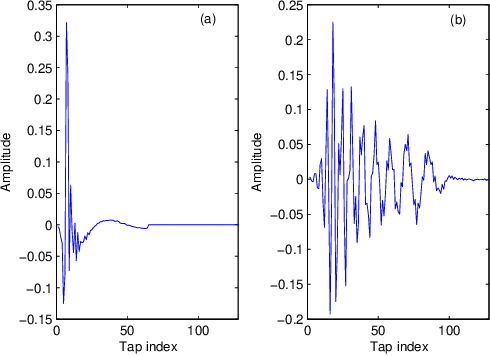
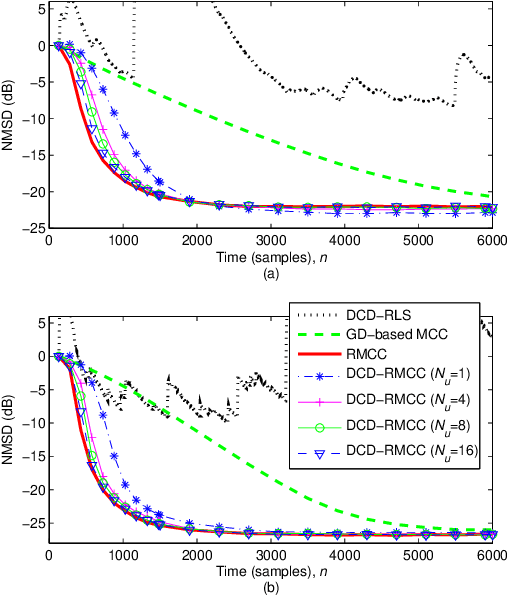
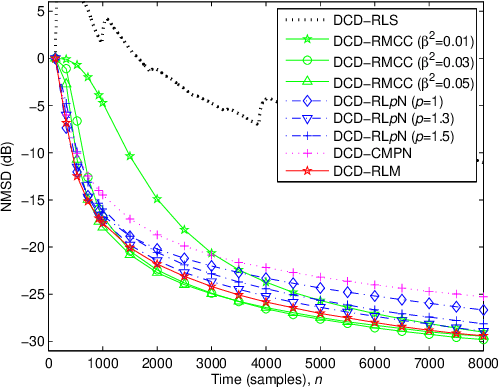
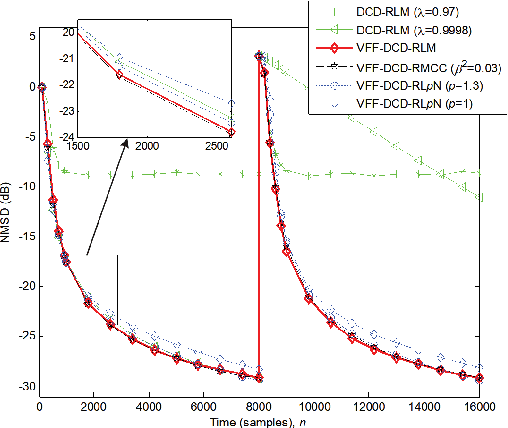
The dichotomous coordinate descent (DCD) algorithm has been successfully used for significant reduction in the complexity of recursive least squares (RLS) algorithms. In this work, we generalize the application of the DCD algorithm to RLS adaptive filtering in impulsive noise scenarios and derive a unified update formula. By employing different robust strategies against impulsive noise, we develop novel computationally efficient DCD-based robust recursive algorithms. Furthermore, to equip the proposed algorithms with the ability to track abrupt changes in unknown systems, a simple variable forgetting factor mechanism is also developed. Simulation results for channel identification scenarios in impulsive noise demonstrate the effectiveness of the proposed algorithms.

Study of Robust Distributed Diffusion RLS Algorithms with Side Information for Adaptive Networks

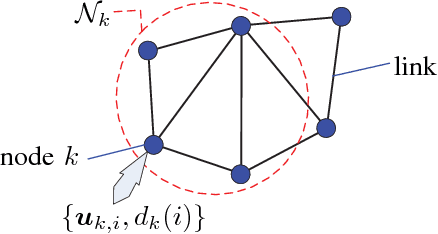
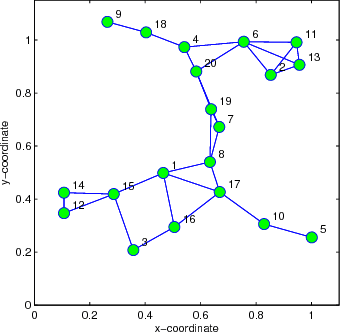
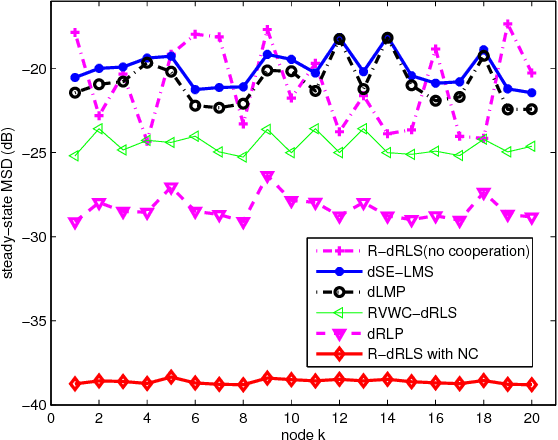
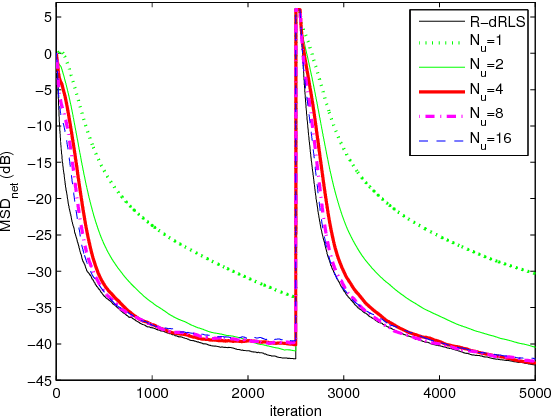
This work develops robust diffusion recursive least squares algorithms to mitigate the performance degradation often experienced in networks of agents in the presence of impulsive noise. The first algorithm minimizes an exponentially weighted least-squares cost function subject to a time-dependent constraint on the squared norm of the intermediate update at each node. A recursive strategy for computing the constraint is proposed using side information from the neighboring nodes to further improve the robustness. We also analyze the mean-square convergence behavior of the proposed algorithm. The second proposed algorithm is a modification of the first one based on the dichotomous coordinate descent iterations. It has a performance similar to that of the former, however its complexity is significantly lower especially when input regressors of agents have a shift structure and it is well suited to practical implementation. Simulations show the superiority of the proposed algorithms over previously reported techniques in various impulsive noise scenarios.

Study of Robust Diffusion Recursive Least Squares Algorithms with Side Information for Networked Agents

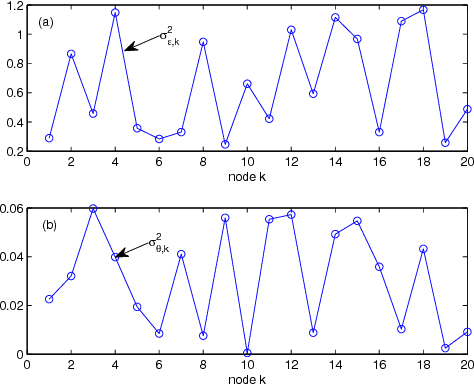
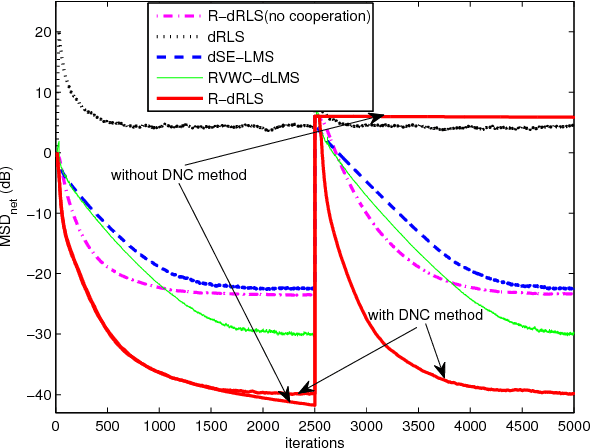
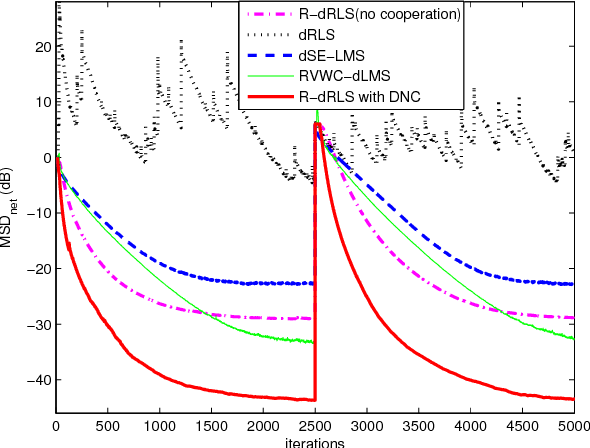
This work develops a robust diffusion recursive least squares algorithm to mitigate the performance degradation often experienced in networks of agents in the presence of impulsive noise. This algorithm minimizes an exponentially weighted least-squares cost function subject to a time-dependent constraint on the squared norm of the intermediate estimate update at each node. With the help of side information, the constraint is recursively updated in a diffusion strategy. Moreover, a control strategy for resetting the constraint is also proposed to retain good tracking capability when the estimated parameters suddenly change. Simulations show the superiority of the proposed algorithm over previously reported techniques in various impulsive noise scenarios.

Study of Sparsity-Aware Subband Adaptive Filtering Algorithms with Adjustable Penalties

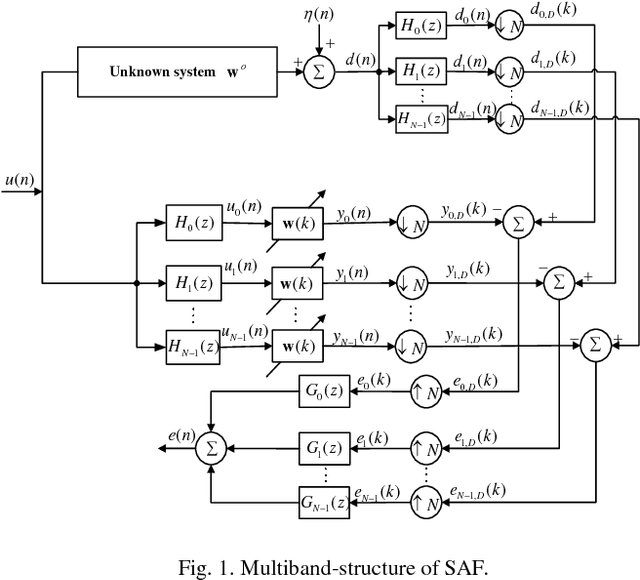
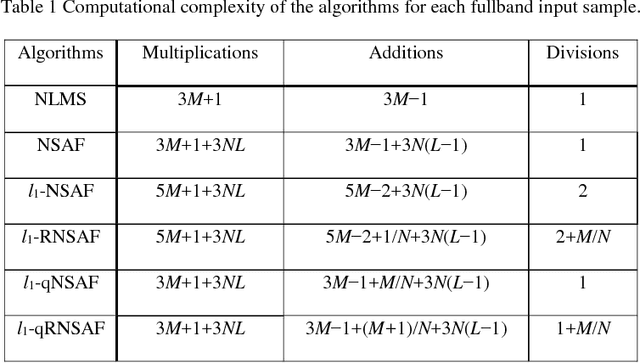
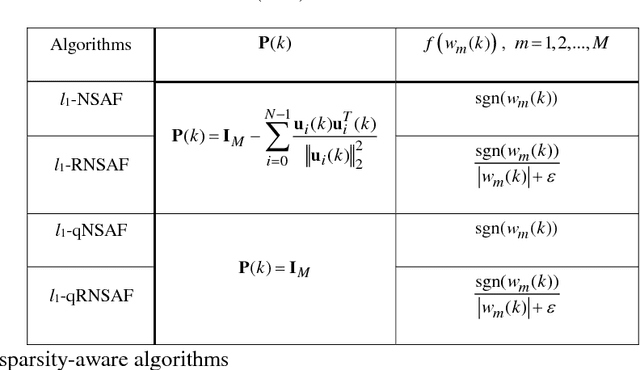
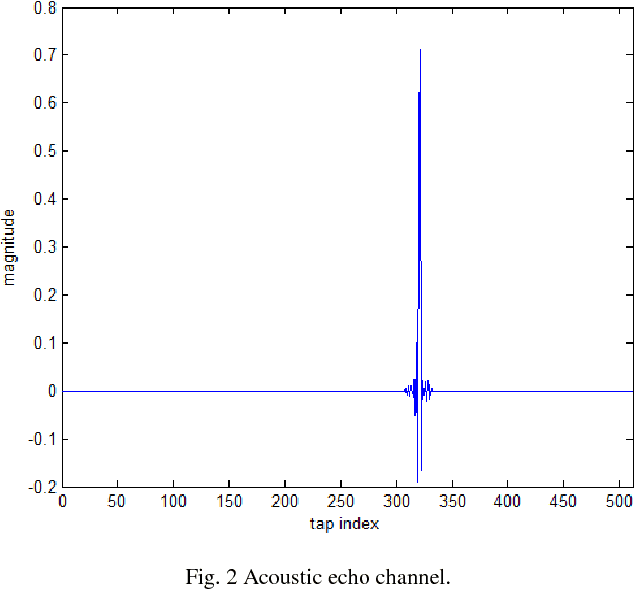
We propose two sparsity-aware normalized subband adaptive filter (NSAF) algorithms by using the gradient descent method to minimize a combination of the original NSAF cost function and the l1-norm penalty function on the filter coefficients. This l1-norm penalty exploits the sparsity of a system in the coefficients update formulation, thus improving the performance when identifying sparse systems. Compared with prior work, the proposed algorithms have lower computational complexity with comparable performance. We study and devise statistical models for these sparsity-aware NSAF algorithms in the mean square sense involving their transient and steady -state behaviors. This study relies on the vectorization argument and the paraunitary assumption imposed on the analysis filter banks, and thus does not restrict the input signal to being Gaussian or having another distribution. In addition, we propose to adjust adaptively the intensity parameter of the sparsity attraction term. Finally, simulation results in sparse system identification demonstrate the effectiveness of our theoretical results.