Study of Sparsity-Aware Subband Adaptive Filtering Algorithms with Adjustable Penalties
Paper and Code
Oct 16, 2018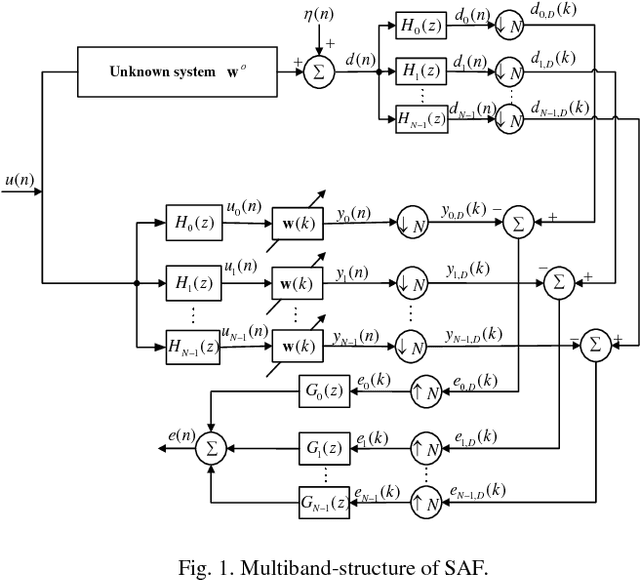
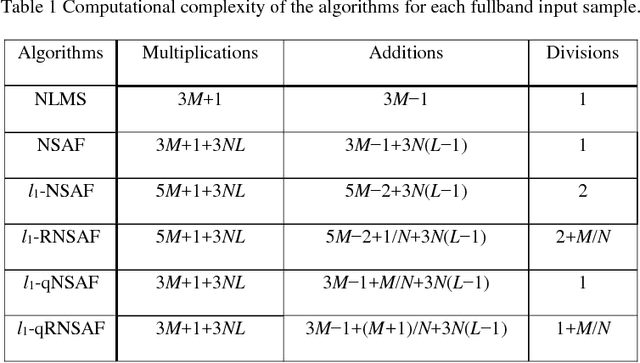
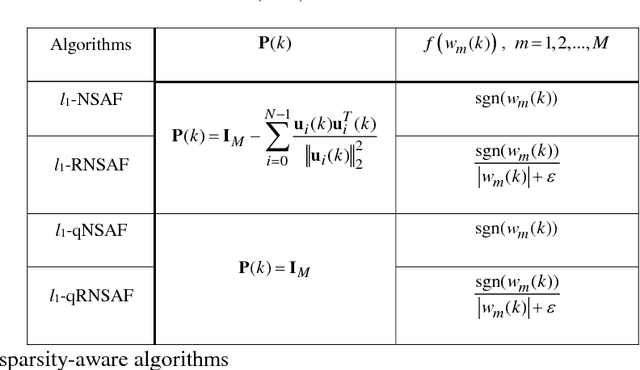
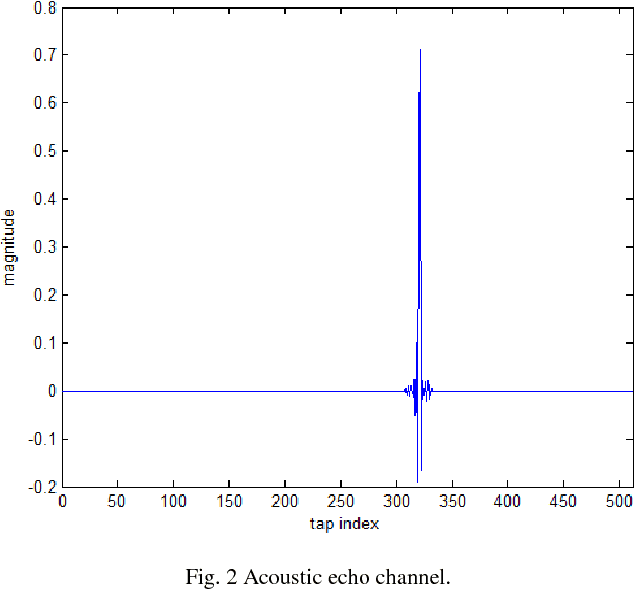
We propose two sparsity-aware normalized subband adaptive filter (NSAF) algorithms by using the gradient descent method to minimize a combination of the original NSAF cost function and the l1-norm penalty function on the filter coefficients. This l1-norm penalty exploits the sparsity of a system in the coefficients update formulation, thus improving the performance when identifying sparse systems. Compared with prior work, the proposed algorithms have lower computational complexity with comparable performance. We study and devise statistical models for these sparsity-aware NSAF algorithms in the mean square sense involving their transient and steady -state behaviors. This study relies on the vectorization argument and the paraunitary assumption imposed on the analysis filter banks, and thus does not restrict the input signal to being Gaussian or having another distribution. In addition, we propose to adjust adaptively the intensity parameter of the sparsity attraction term. Finally, simulation results in sparse system identification demonstrate the effectiveness of our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge