UHDRes: Ultra-High-Definition Image Restoration via Dual-Domain Decoupled Spectral Modulation

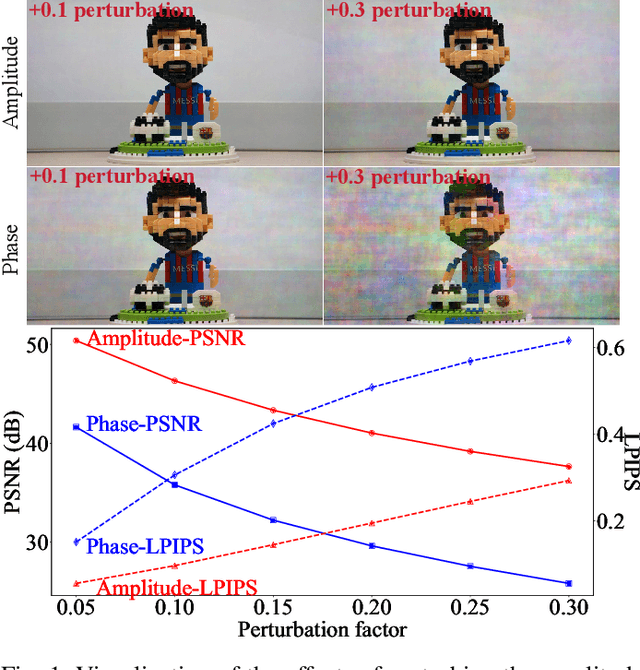
Ultra-high-definition (UHD) images often suffer from severe degradations such as blur, haze, rain, or low-light conditions, which pose significant challenges for image restoration due to their high resolution and computational demands. In this paper, we propose UHDRes, a novel lightweight dual-domain decoupled spectral modulation framework for UHD image restoration. It explicitly models the amplitude spectrum via lightweight spectrum-domain modulation, while restoring phase implicitly through spatial-domain refinement. We introduce the spatio-spectral fusion mechanism, which first employs a multi-scale context aggregator to extract local and global spatial features, and then performs spectral modulation in a decoupled manner. It explicitly enhances amplitude features in the frequency domain while implicitly restoring phase information through spatial refinement. Additionally, a shared gated feed-forward network is designed to efficiently promote feature interaction through shared-parameter convolutions and adaptive gating mechanisms. Extensive experimental comparisons on five public UHD benchmarks demonstrate that our UHDRes achieves the state-of-the-art restoration performance with only 400K parameters, while significantly reducing inference latency and memory usage. The codes and models are available at https://github.com/Zhao0100/UHDRes.

Study of Robust Distributed Diffusion RLS Algorithms with Side Information for Adaptive Networks

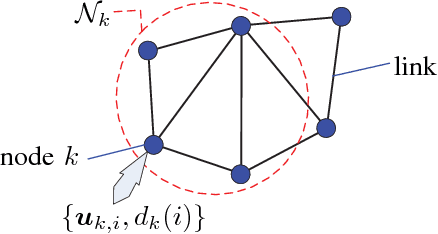
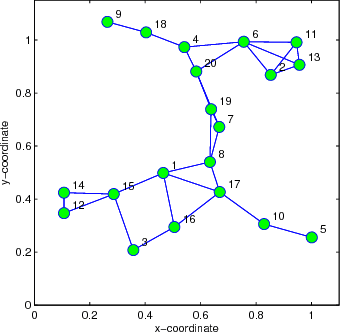
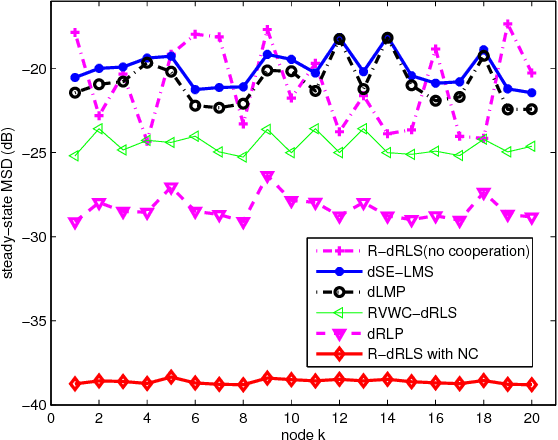
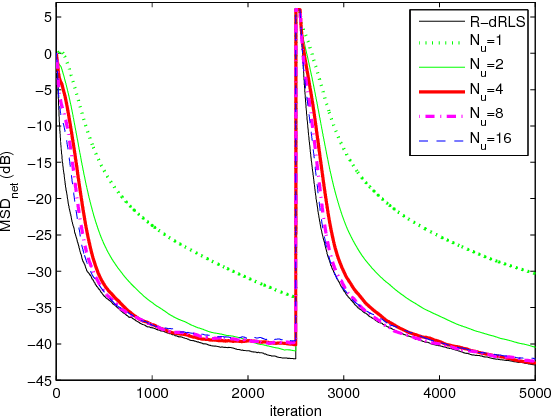
This work develops robust diffusion recursive least squares algorithms to mitigate the performance degradation often experienced in networks of agents in the presence of impulsive noise. The first algorithm minimizes an exponentially weighted least-squares cost function subject to a time-dependent constraint on the squared norm of the intermediate update at each node. A recursive strategy for computing the constraint is proposed using side information from the neighboring nodes to further improve the robustness. We also analyze the mean-square convergence behavior of the proposed algorithm. The second proposed algorithm is a modification of the first one based on the dichotomous coordinate descent iterations. It has a performance similar to that of the former, however its complexity is significantly lower especially when input regressors of agents have a shift structure and it is well suited to practical implementation. Simulations show the superiority of the proposed algorithms over previously reported techniques in various impulsive noise scenarios.

Study of Sparsity-Aware Subband Adaptive Filtering Algorithms with Adjustable Penalties

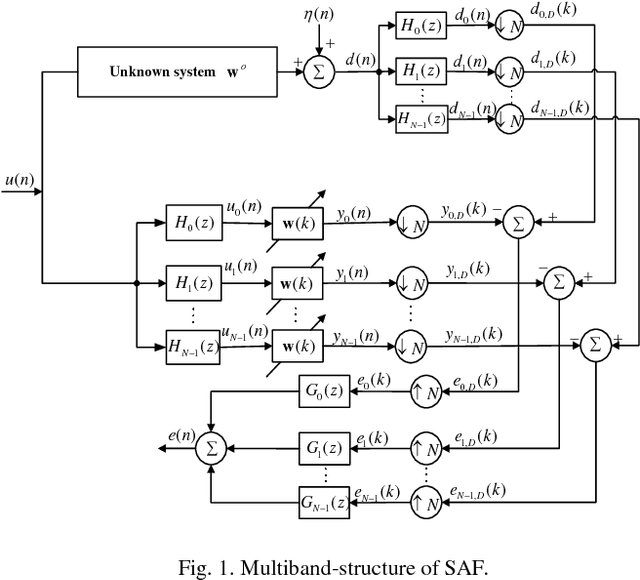
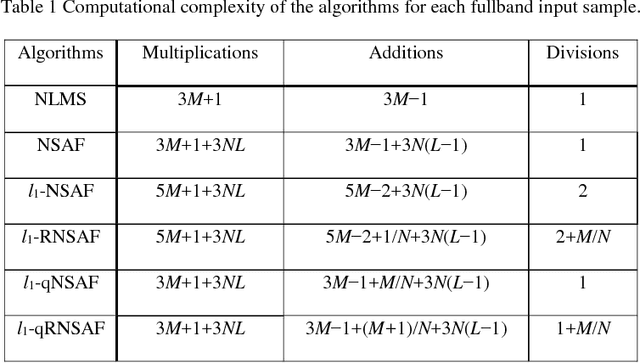
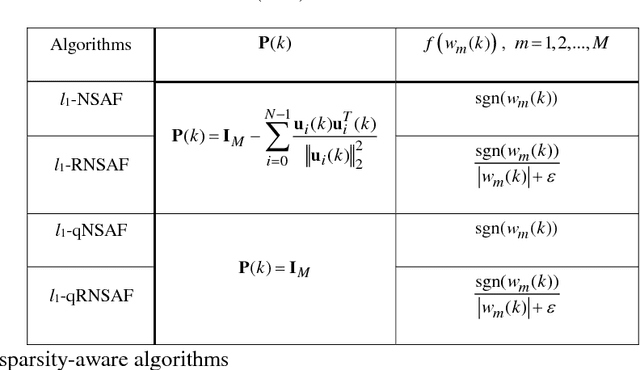
We propose two sparsity-aware normalized subband adaptive filter (NSAF) algorithms by using the gradient descent method to minimize a combination of the original NSAF cost function and the l1-norm penalty function on the filter coefficients. This l1-norm penalty exploits the sparsity of a system in the coefficients update formulation, thus improving the performance when identifying sparse systems. Compared with prior work, the proposed algorithms have lower computational complexity with comparable performance. We study and devise statistical models for these sparsity-aware NSAF algorithms in the mean square sense involving their transient and steady -state behaviors. This study relies on the vectorization argument and the paraunitary assumption imposed on the analysis filter banks, and thus does not restrict the input signal to being Gaussian or having another distribution. In addition, we propose to adjust adaptively the intensity parameter of the sparsity attraction term. Finally, simulation results in sparse system identification demonstrate the effectiveness of our theoretical results.