Study of Robust Sparsity-Aware RLS algorithms with Jointly-Optimized Parameters for Impulsive Noise Environments

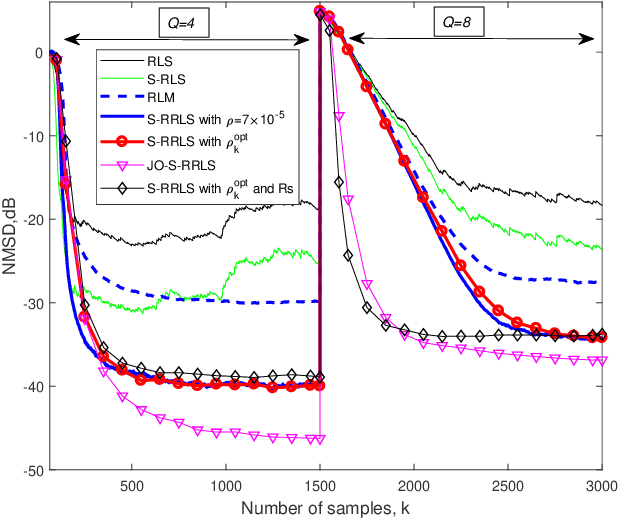
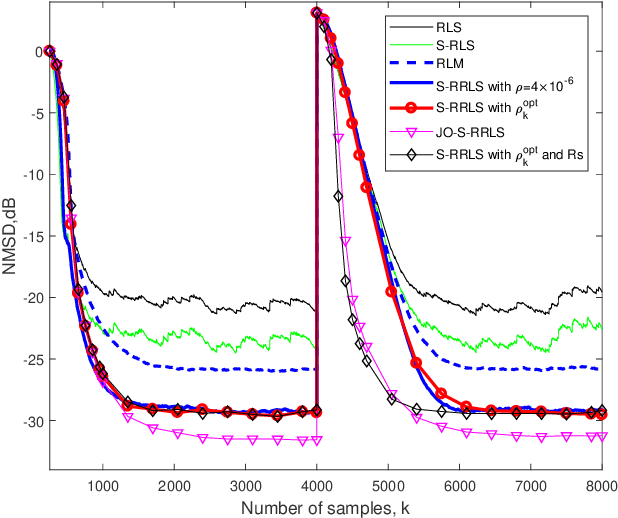
This paper proposes a unified sparsity-aware robust recursive least-squares RLS (S-RRLS) algorithm for the identification of sparse systems under impulsive noise. The proposed algorithm generalizes multiple algorithms only by replacing the specified criterion of robustness and sparsity-aware penalty. Furthermore, by jointly optimizing the forgetting factor and the sparsity penalty parameter, we develop the jointly-optimized S-RRLS (JO-S-RRLS) algorithm, which not only exhibits low misadjustment but also can track well sudden changes of a sparse system. Simulations in impulsive noise scenarios demonstrate that the proposed S-RRLS and JO-S-RRLS algorithms outperform existing techniques.

Robust DCD-Based Recursive Adaptive Algorithms

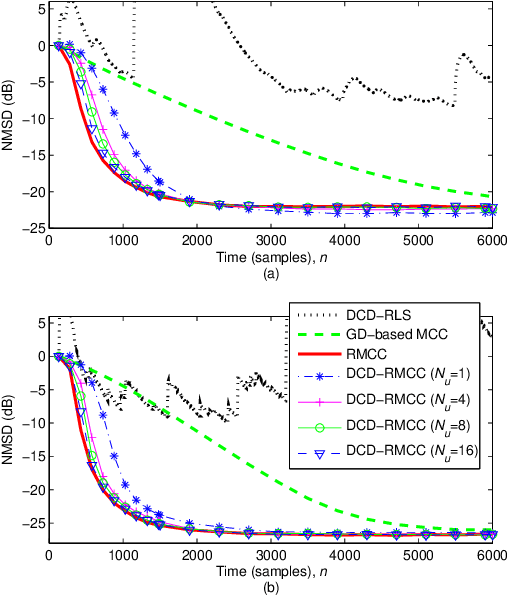
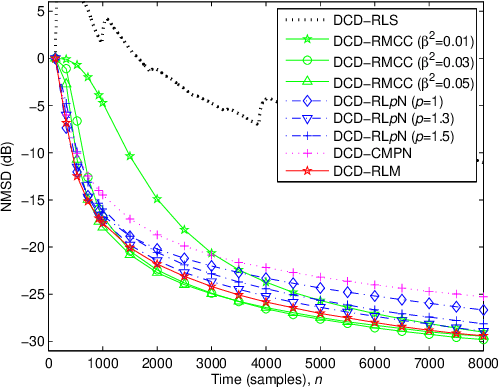
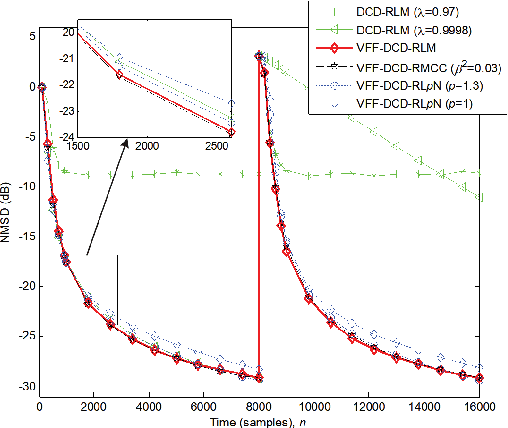
The dichotomous coordinate descent (DCD) algorithm has been successfully used for significant reduction in the complexity of recursive least squares (RLS) algorithms. In this work, we generalize the application of the DCD algorithm to RLS adaptive filtering in impulsive noise scenarios and derive a unified update formula. By employing different robust strategies against impulsive noise, we develop novel computationally efficient DCD-based robust recursive algorithms. Furthermore, to equip the proposed algorithms with the ability to track abrupt changes in unknown systems, a simple variable forgetting factor mechanism is also developed. Simulation results for channel identification scenarios in impulsive noise demonstrate the effectiveness of the proposed algorithms.

Study of Robust Distributed Diffusion RLS Algorithms with Side Information for Adaptive Networks

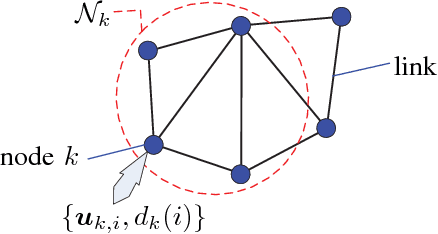
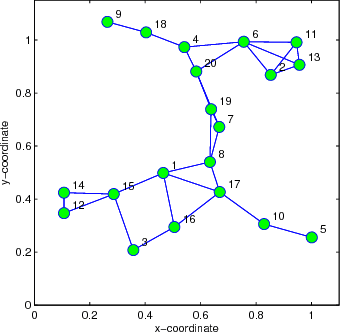
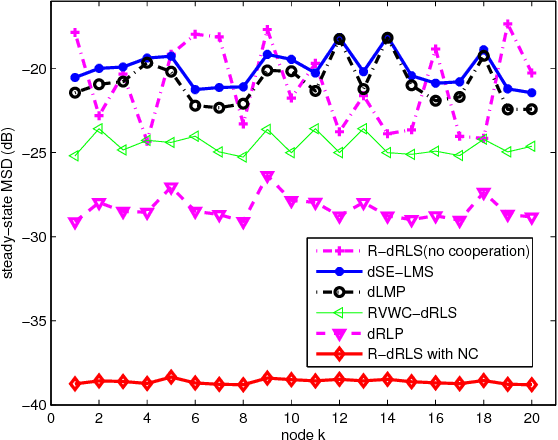
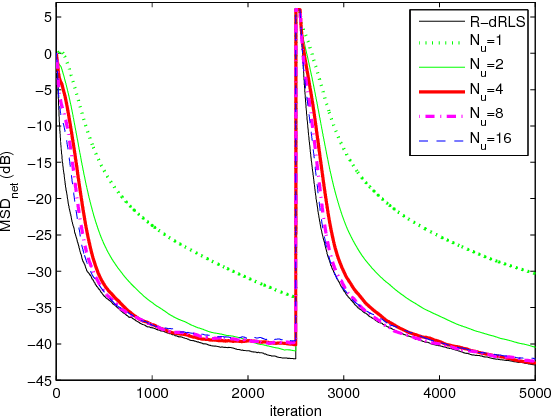
This work develops robust diffusion recursive least squares algorithms to mitigate the performance degradation often experienced in networks of agents in the presence of impulsive noise. The first algorithm minimizes an exponentially weighted least-squares cost function subject to a time-dependent constraint on the squared norm of the intermediate update at each node. A recursive strategy for computing the constraint is proposed using side information from the neighboring nodes to further improve the robustness. We also analyze the mean-square convergence behavior of the proposed algorithm. The second proposed algorithm is a modification of the first one based on the dichotomous coordinate descent iterations. It has a performance similar to that of the former, however its complexity is significantly lower especially when input regressors of agents have a shift structure and it is well suited to practical implementation. Simulations show the superiority of the proposed algorithms over previously reported techniques in various impulsive noise scenarios.

Study of Robust Diffusion Recursive Least Squares Algorithms with Side Information for Networked Agents

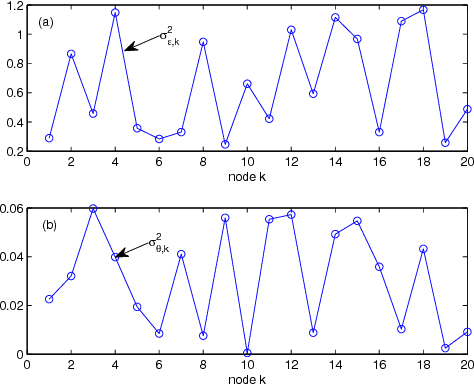
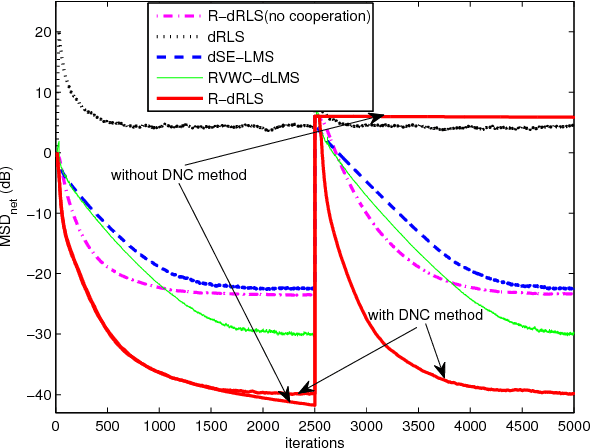
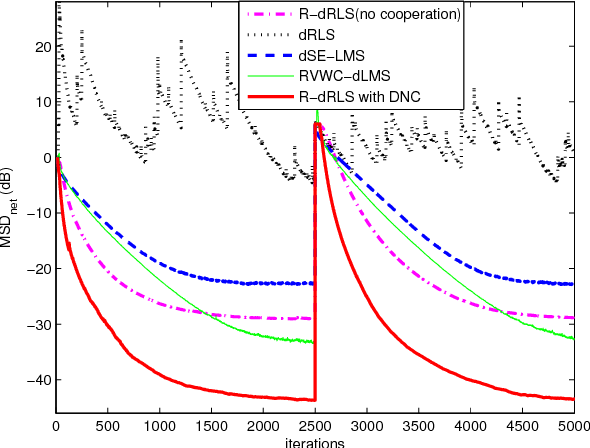
This work develops a robust diffusion recursive least squares algorithm to mitigate the performance degradation often experienced in networks of agents in the presence of impulsive noise. This algorithm minimizes an exponentially weighted least-squares cost function subject to a time-dependent constraint on the squared norm of the intermediate estimate update at each node. With the help of side information, the constraint is recursively updated in a diffusion strategy. Moreover, a control strategy for resetting the constraint is also proposed to retain good tracking capability when the estimated parameters suddenly change. Simulations show the superiority of the proposed algorithm over previously reported techniques in various impulsive noise scenarios.