Observation of high-energy neutrinos from the Galactic plane

The origin of high-energy cosmic rays, atomic nuclei that continuously impact Earth's atmosphere, has been a mystery for over a century. Due to deflection in interstellar magnetic fields, cosmic rays from the Milky Way arrive at Earth from random directions. However, near their sources and during propagation, cosmic rays interact with matter and produce high-energy neutrinos. We search for neutrino emission using machine learning techniques applied to ten years of data from the IceCube Neutrino Observatory. We identify neutrino emission from the Galactic plane at the 4.5$\sigma$ level of significance, by comparing diffuse emission models to a background-only hypothesis. The signal is consistent with modeled diffuse emission from the Galactic plane, but could also arise from a population of unresolved point sources.

Graph Neural Networks for Low-Energy Event Classification & Reconstruction in IceCube

IceCube, a cubic-kilometer array of optical sensors built to detect atmospheric and astrophysical neutrinos between 1 GeV and 1 PeV, is deployed 1.45 km to 2.45 km below the surface of the ice sheet at the South Pole. The classification and reconstruction of events from the in-ice detectors play a central role in the analysis of data from IceCube. Reconstructing and classifying events is a challenge due to the irregular detector geometry, inhomogeneous scattering and absorption of light in the ice and, below 100 GeV, the relatively low number of signal photons produced per event. To address this challenge, it is possible to represent IceCube events as point cloud graphs and use a Graph Neural Network (GNN) as the classification and reconstruction method. The GNN is capable of distinguishing neutrino events from cosmic-ray backgrounds, classifying different neutrino event types, and reconstructing the deposited energy, direction and interaction vertex. Based on simulation, we provide a comparison in the 1-100 GeV energy range to the current state-of-the-art maximum likelihood techniques used in current IceCube analyses, including the effects of known systematic uncertainties. For neutrino event classification, the GNN increases the signal efficiency by 18% at a fixed false positive rate (FPR), compared to current IceCube methods. Alternatively, the GNN offers a reduction of the FPR by over a factor 8 (to below half a percent) at a fixed signal efficiency. For the reconstruction of energy, direction, and interaction vertex, the resolution improves by an average of 13%-20% compared to current maximum likelihood techniques in the energy range of 1-30 GeV. The GNN, when run on a GPU, is capable of processing IceCube events at a rate nearly double of the median IceCube trigger rate of 2.7 kHz, which opens the possibility of using low energy neutrinos in online searches for transient events.

Study of Robust Sparsity-Aware RLS algorithms with Jointly-Optimized Parameters for Impulsive Noise Environments

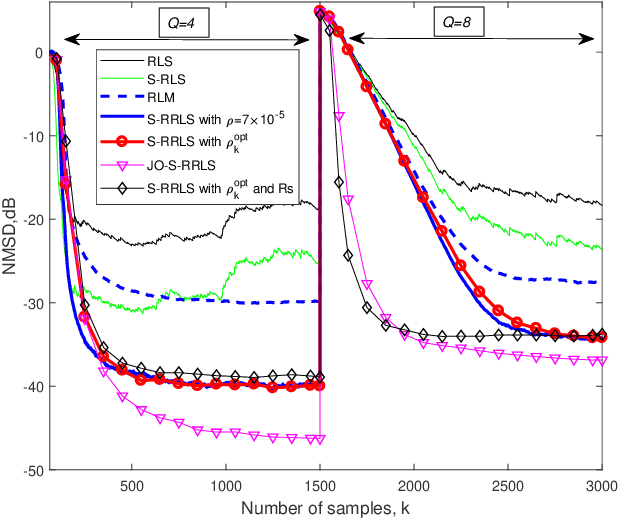
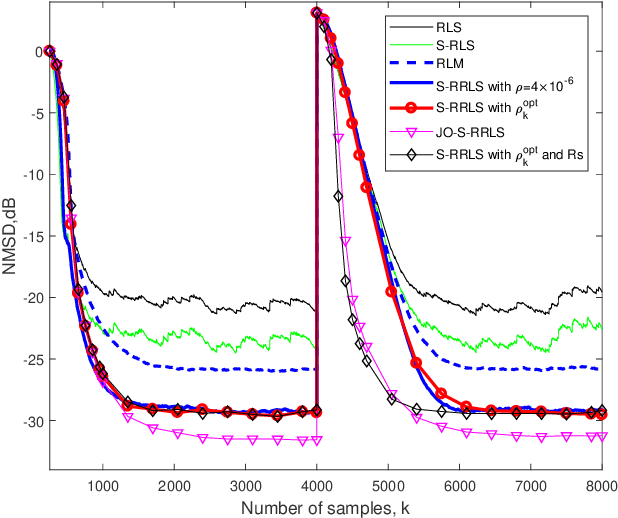
This paper proposes a unified sparsity-aware robust recursive least-squares RLS (S-RRLS) algorithm for the identification of sparse systems under impulsive noise. The proposed algorithm generalizes multiple algorithms only by replacing the specified criterion of robustness and sparsity-aware penalty. Furthermore, by jointly optimizing the forgetting factor and the sparsity penalty parameter, we develop the jointly-optimized S-RRLS (JO-S-RRLS) algorithm, which not only exhibits low misadjustment but also can track well sudden changes of a sparse system. Simulations in impulsive noise scenarios demonstrate that the proposed S-RRLS and JO-S-RRLS algorithms outperform existing techniques.

Study of filtered-x logarithmic recursive least $p$-power algorithm

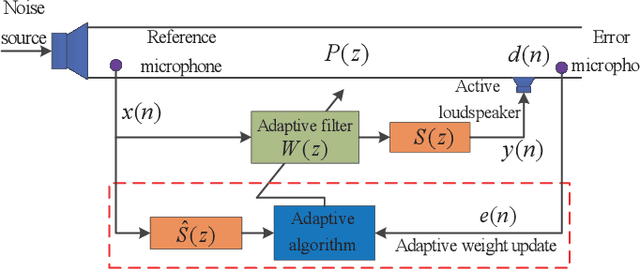
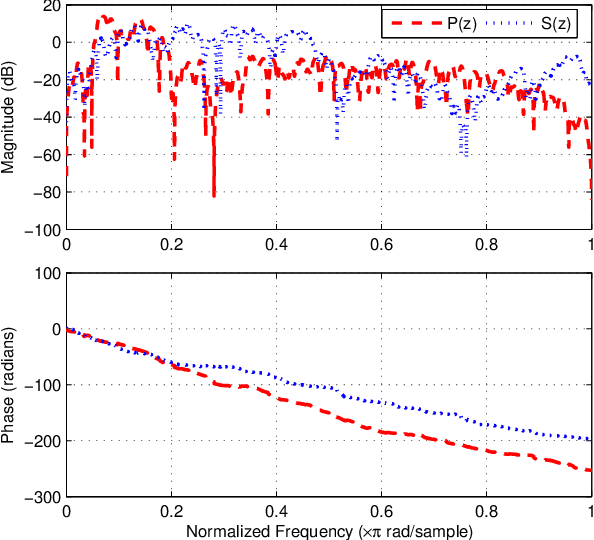
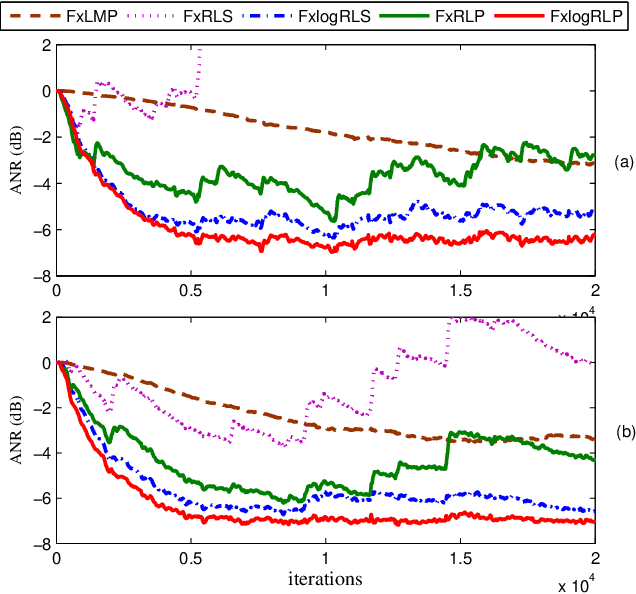
For active impulsive noise control, a filtered-x recursive least $p$-power (FxRLP) algorithm is proposed by minimizing the weighted summation of the $p$-power of the \emph{a posteriori} errors. Since the characteristic of the target noise is investigated, the FxRLP algorithm achieves good performance and robustness. To obtain a better performance, we develop a filtered-x logarithmic recursive least $p$-power (FxlogRLP) algorithm which integrates the $p$-order moment with the logarithmic-order moment. Simulation results demonstrate that the FxlogRLP algorithm is superior to the existing algorithms in terms of convergence rate and noise reduction.

Recovery Conditions of Sparse Signals Using Orthogonal Least Squares-Type Algorithms

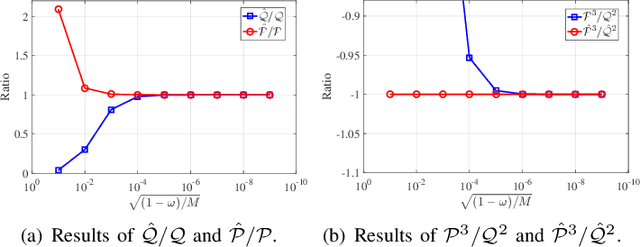
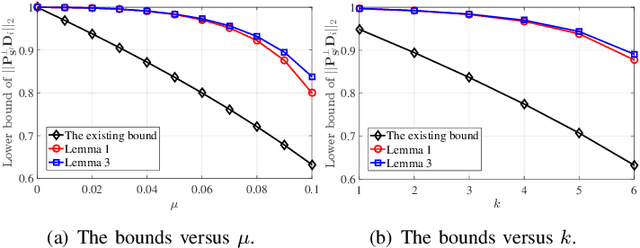
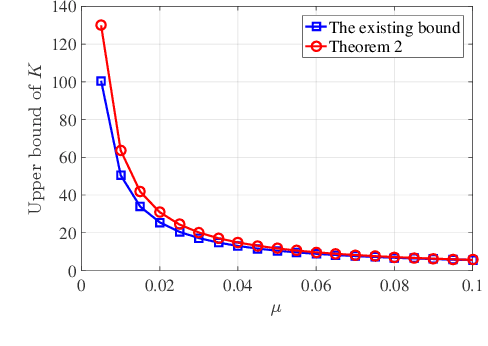
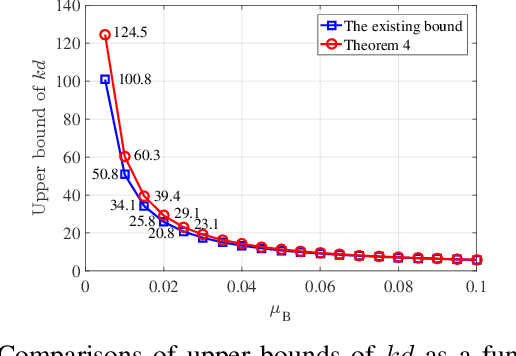
Orthogonal least squares (OLS)-type algorithms are efficient in reconstructing sparse signals, which include the well-known OLS, multiple OLS (MOLS) and block OLS (BOLS). In this paper, we first investigate the noiseless exact recovery conditions of these algorithms. Specifically, based on mutual incoherence property (MIP), we provide theoretical analysis of OLS and MOLS to ensure that the correct nonzero support can be selected during the iterative procedure. Nevertheless, theoretical analysis for BOLS utilizes the block-MIP to deal with the block sparsity. Furthermore, the noiseless MIP-based analyses are extended to the noisy scenario. Our results indicate that for K-sparse signals, when MIP or SNR satisfies certain conditions, OLS and MOLS obtain reliable reconstruction in at most K iterations, while BOLS succeeds in at most (K/d) iterations where d is the block length. It is shown that our derived theoretical results improve the existing ones, which are verified by simulation tests.

A Convolutional Neural Network based Cascade Reconstruction for the IceCube Neutrino Observatory

Continued improvements on existing reconstruction methods are vital to the success of high-energy physics experiments, such as the IceCube Neutrino Observatory. In IceCube, further challenges arise as the detector is situated at the geographic South Pole where computational resources are limited. However, to perform real-time analyses and to issue alerts to telescopes around the world, powerful and fast reconstruction methods are desired. Deep neural networks can be extremely powerful, and their usage is computationally inexpensive once the networks are trained. These characteristics make a deep learning-based approach an excellent candidate for the application in IceCube. A reconstruction method based on convolutional architectures and hexagonally shaped kernels is presented. The presented method is robust towards systematic uncertainties in the simulation and has been tested on experimental data. In comparison to standard reconstruction methods in IceCube, it can improve upon the reconstruction accuracy, while reducing the time necessary to run the reconstruction by two to three orders of magnitude.

Robust DCD-Based Recursive Adaptive Algorithms

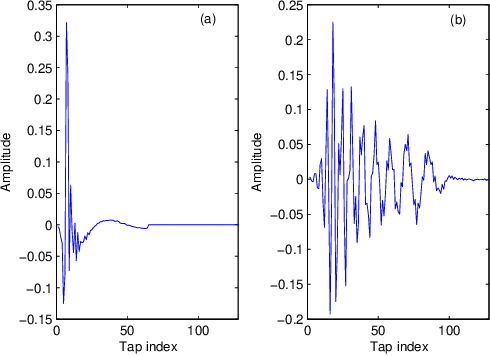
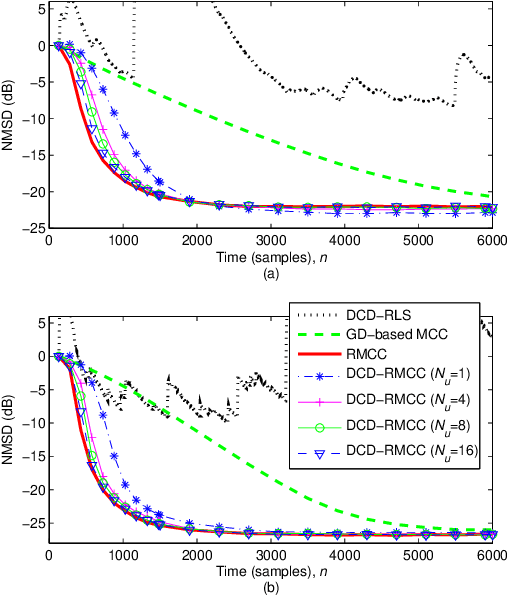
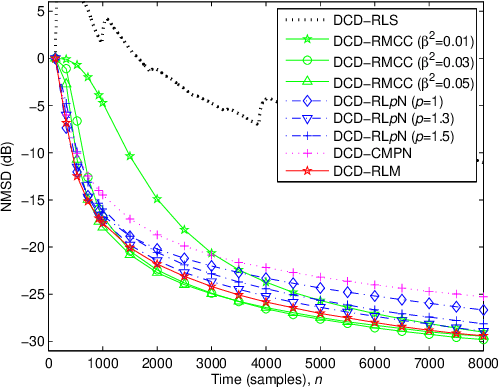
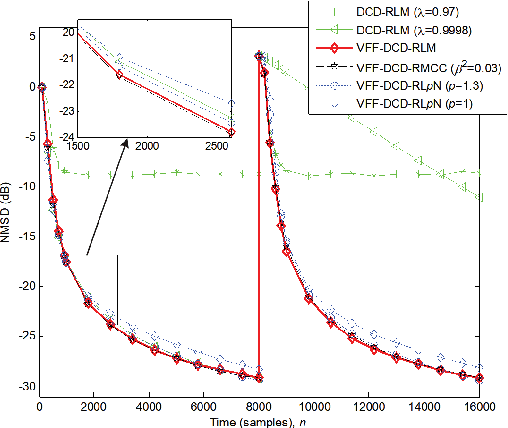
The dichotomous coordinate descent (DCD) algorithm has been successfully used for significant reduction in the complexity of recursive least squares (RLS) algorithms. In this work, we generalize the application of the DCD algorithm to RLS adaptive filtering in impulsive noise scenarios and derive a unified update formula. By employing different robust strategies against impulsive noise, we develop novel computationally efficient DCD-based robust recursive algorithms. Furthermore, to equip the proposed algorithms with the ability to track abrupt changes in unknown systems, a simple variable forgetting factor mechanism is also developed. Simulation results for channel identification scenarios in impulsive noise demonstrate the effectiveness of the proposed algorithms.

Study of Robust Distributed Diffusion RLS Algorithms with Side Information for Adaptive Networks

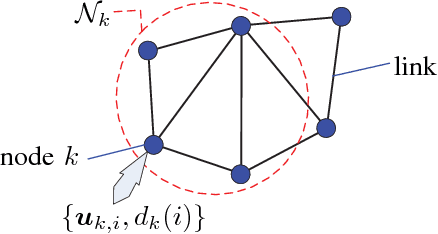
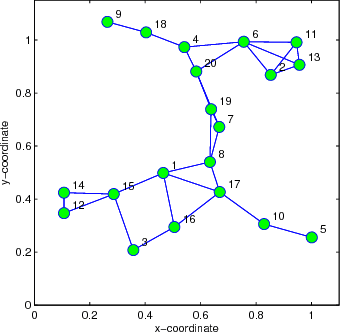
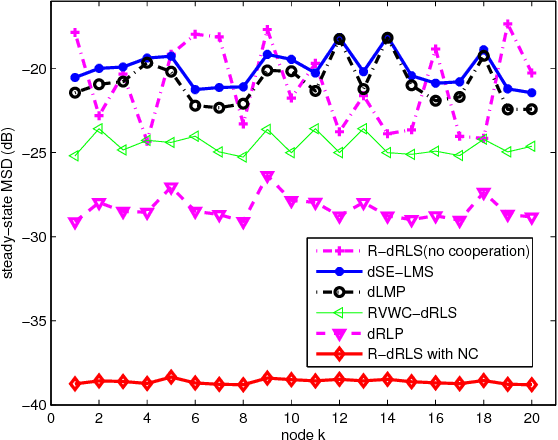
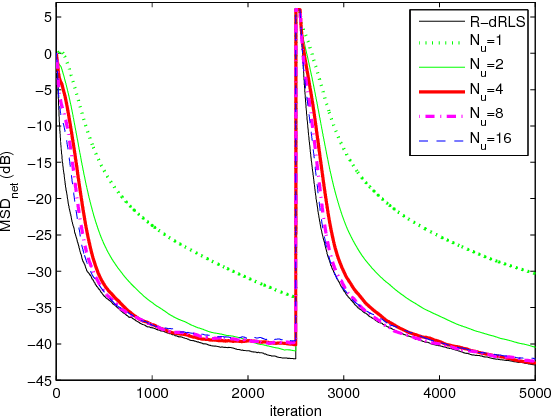
This work develops robust diffusion recursive least squares algorithms to mitigate the performance degradation often experienced in networks of agents in the presence of impulsive noise. The first algorithm minimizes an exponentially weighted least-squares cost function subject to a time-dependent constraint on the squared norm of the intermediate update at each node. A recursive strategy for computing the constraint is proposed using side information from the neighboring nodes to further improve the robustness. We also analyze the mean-square convergence behavior of the proposed algorithm. The second proposed algorithm is a modification of the first one based on the dichotomous coordinate descent iterations. It has a performance similar to that of the former, however its complexity is significantly lower especially when input regressors of agents have a shift structure and it is well suited to practical implementation. Simulations show the superiority of the proposed algorithms over previously reported techniques in various impulsive noise scenarios.