Foresee and Act Ahead: Task Prediction and Pre-Scheduling Enabled Efficient Robotic Warehousing

In warehousing systems, to enhance logistical efficiency amid surging demand volumes, much focus is placed on how to reasonably allocate tasks to robots. However, the robots labor is still inevitably wasted to some extent. In response to this, we propose a pre-scheduling enhanced warehousing framework that predicts task flow and acts in advance. It consists of task flow prediction and hybrid tasks allocation. For task prediction, we notice that it is possible to provide a spatio-temporal representation of task flow, so we introduce a periodicity-decoupled mechanism tailored for the generation patterns of aggregated orders, and then further extract spatial features of task distribution with novel combination of graph structures. In hybrid tasks allocation, we consider the known tasks and predicted future tasks simultaneously and optimize the allocation dynamically. In addition, we consider factors such as predicted task uncertainty and sector-level efficiency evaluation in warehousing to realize more balanced and rational allocations. We validate our task prediction model across actual datasets derived from real factories, achieving SOTA performance. Furthermore, we implement our compelte scheduling system in a real-world robotic warehouse for months of lifelong validation, demonstrating large improvements in key metrics of warehousing, such as empty running rate, by more than 50%.

Extraction of In-Phase and Quadrature Components by Time-Encoding Sampling

Time encoding machine (TEM) is a biologically-inspired scheme to perform signal sampling using timing. In this paper, we study its application to the sampling of bandpass signals. We propose an integrate-and-fire TEM scheme by which the in-phase (I) and quadrature (Q) components are extracted through reconstruction. We design the TEM according to the signal bandwidth and amplitude instead of upper-edge frequency and amplitude as in the case of bandlimited/lowpass signals. We show that the I and Q components can be perfectly reconstructed from the TEM measurements if the minimum firing rate is equal to the Landau's rate of the signal. For the reconstruction of I and Q components, we develop an alternating projection onto convex sets (POCS) algorithm in which two POCS algorithms are alternately iterated. For the algorithm analysis, we define a solution space of vector-valued signals and prove that the proposed reconstruction algorithm converges to the correct unique solution in the noiseless case. The proposed TEM can operate regardless of the center frequencies of the bandpass signals. This is quite different from traditional bandpass sampling, where the center frequency should be carefully allocated for Landau's rate and its variations have the negative effect on the sampling performance. In addition, the proposed TEM achieves certain reconstructed signal-to-noise-plus-distortion ratios for small firing rates in thermal noise, which is unavoidably present and will be aliased to the Nyquist band in the traditional sampling such that high sampling rates are required. We demonstrate the reconstruction performance and substantiate our claims via simulation experiments.

Beyond Imitation: A Life-long Policy Learning Framework for Path Tracking Control of Autonomous Driving

Model-free learning-based control methods have recently shown significant advantages over traditional control methods in avoiding complex vehicle characteristic estimation and parameter tuning. As a primary policy learning method, imitation learning (IL) is capable of learning control policies directly from expert demonstrations. However, the performance of IL policies is highly dependent on the data sufficiency and quality of the demonstrations. To alleviate the above problems of IL-based policies, a lifelong policy learning (LLPL) framework is proposed in this paper, which extends the IL scheme with lifelong learning (LLL). First, a novel IL-based model-free control policy learning method for path tracking is introduced. Even with imperfect demonstration, the optimal control policy can be learned directly from historical driving data. Second, by using the LLL method, the pre-trained IL policy can be safely updated and fine-tuned with incremental execution knowledge. Third, a knowledge evaluation method for policy learning is introduced to avoid learning redundant or inferior knowledge, thus ensuring the performance improvement of online policy learning. Experiments are conducted using a high-fidelity vehicle dynamic model in various scenarios to evaluate the performance of the proposed method. The results show that the proposed LLPL framework can continuously improve the policy performance with collected incremental driving data, and achieves the best accuracy and control smoothness compared to other baseline methods after evolving on a 7 km curved road. Through learning and evaluation with noisy real-life data collected in an off-road environment, the proposed LLPL framework also demonstrates its applicability in learning and evolving in real-life scenarios.

Study of filtered-x logarithmic recursive least $p$-power algorithm

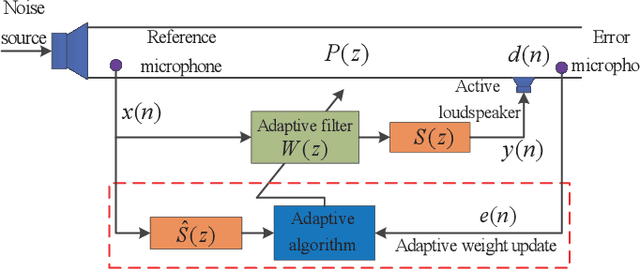
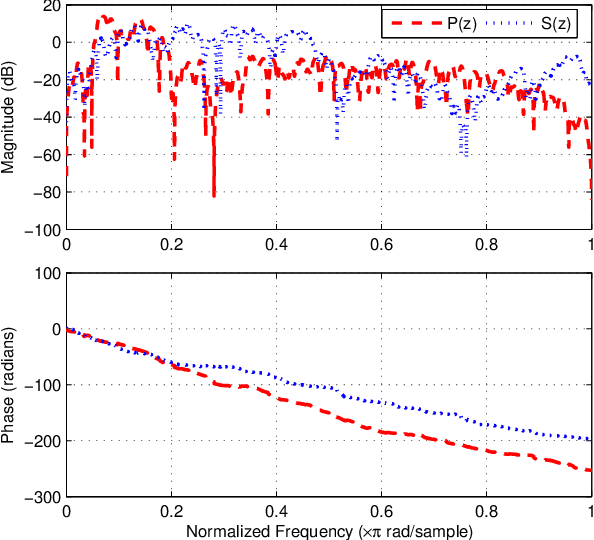
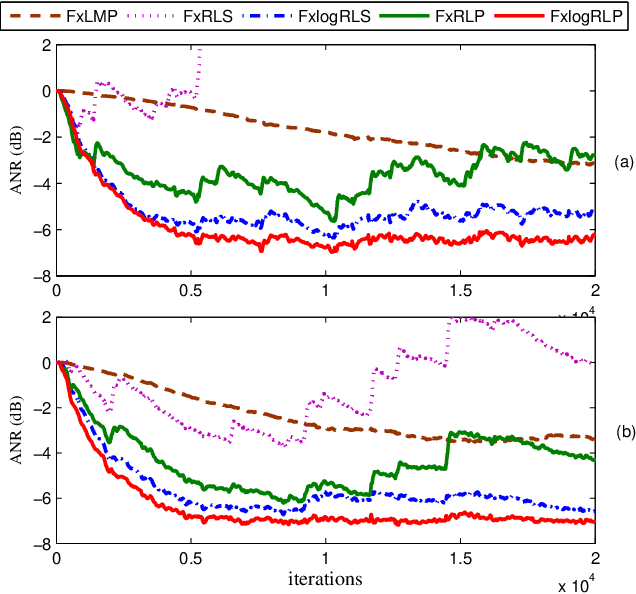
For active impulsive noise control, a filtered-x recursive least $p$-power (FxRLP) algorithm is proposed by minimizing the weighted summation of the $p$-power of the \emph{a posteriori} errors. Since the characteristic of the target noise is investigated, the FxRLP algorithm achieves good performance and robustness. To obtain a better performance, we develop a filtered-x logarithmic recursive least $p$-power (FxlogRLP) algorithm which integrates the $p$-order moment with the logarithmic-order moment. Simulation results demonstrate that the FxlogRLP algorithm is superior to the existing algorithms in terms of convergence rate and noise reduction.