Y. Cui
Recovery Conditions of Sparse Signals Using Orthogonal Least Squares-Type Algorithms
Jan 13, 2022
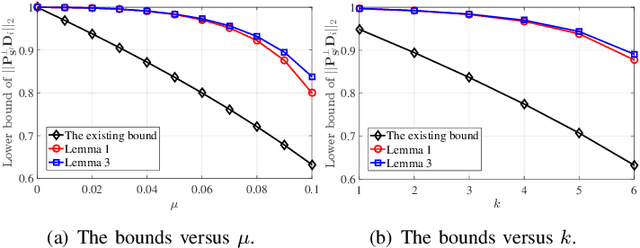
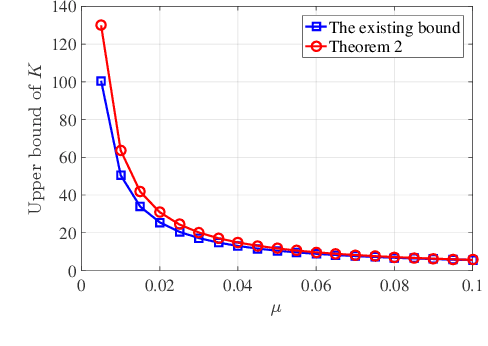
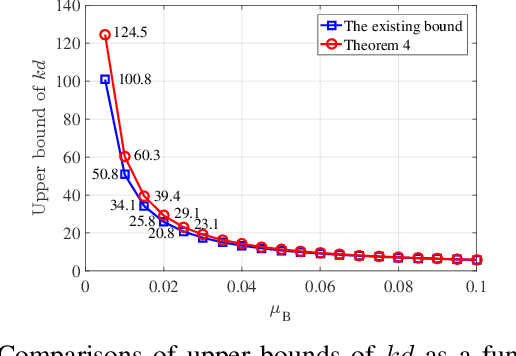
Abstract:Orthogonal least squares (OLS)-type algorithms are efficient in reconstructing sparse signals, which include the well-known OLS, multiple OLS (MOLS) and block OLS (BOLS). In this paper, we first investigate the noiseless exact recovery conditions of these algorithms. Specifically, based on mutual incoherence property (MIP), we provide theoretical analysis of OLS and MOLS to ensure that the correct nonzero support can be selected during the iterative procedure. Nevertheless, theoretical analysis for BOLS utilizes the block-MIP to deal with the block sparsity. Furthermore, the noiseless MIP-based analyses are extended to the noisy scenario. Our results indicate that for K-sparse signals, when MIP or SNR satisfies certain conditions, OLS and MOLS obtain reliable reconstruction in at most K iterations, while BOLS succeeds in at most (K/d) iterations where d is the block length. It is shown that our derived theoretical results improve the existing ones, which are verified by simulation tests.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge