Impression Allocation and Policy Search in Display Advertising

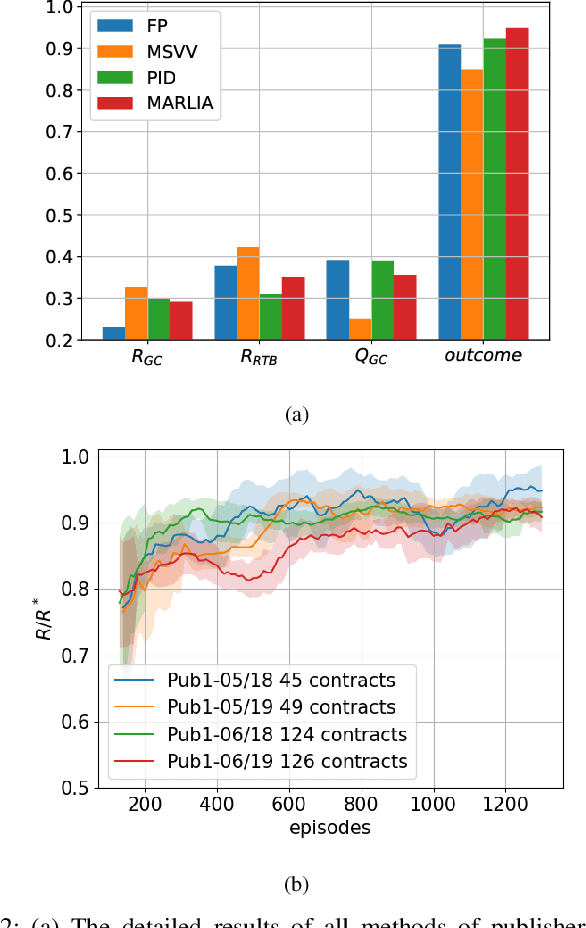
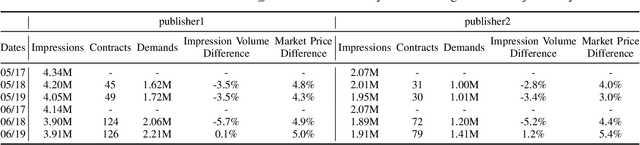
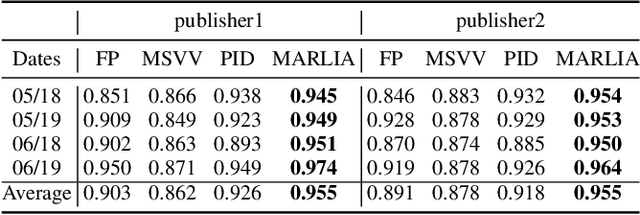
In online display advertising, guaranteed contracts and real-time bidding (RTB) are two major ways to sell impressions for a publisher. For large publishers, simultaneously selling impressions through both guaranteed contracts and in-house RTB has become a popular choice. Generally speaking, a publisher needs to derive an impression allocation strategy between guaranteed contracts and RTB to maximize its overall outcome (e.g., revenue and/or impression quality). However, deriving the optimal strategy is not a trivial task, e.g., the strategy should encourage incentive compatibility in RTB and tackle common challenges in real-world applications such as unstable traffic patterns (e.g., impression volume and bid landscape changing). In this paper, we formulate impression allocation as an auction problem where each guaranteed contract submits virtual bids for individual impressions. With this formulation, we derive the optimal bidding functions for the guaranteed contracts, which result in the optimal impression allocation. In order to address the unstable traffic pattern challenge and achieve the optimal overall outcome, we propose a multi-agent reinforcement learning method to adjust the bids from each guaranteed contract, which is simple, converging efficiently and scalable. The experiments conducted on real-world datasets demonstrate the effectiveness of our method.

Budget Constrained Bidding by Model-free Reinforcement Learning in Display Advertising

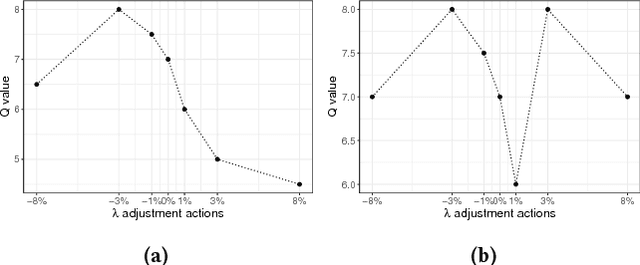
Real-time bidding (RTB) is an important mechanism in online display advertising, where a proper bid for each page view plays an essential role for good marketing results. Budget constrained bidding is a typical scenario in RTB where the advertisers hope to maximize the total value of the winning impressions under a pre-set budget constraint. However, the optimal bidding strategy is hard to be derived due to the complexity and volatility of the auction environment. To address these challenges, in this paper, we formulate budget constrained bidding as a Markov Decision Process and propose a model-free reinforcement learning framework to resolve the optimization problem. Our analysis shows that the immediate reward from environment is misleading under a critical resource constraint. Therefore, we innovate a reward function design methodology for the reinforcement learning problems with constraints. Based on the new reward design, we employ a deep neural network to learn the appropriate reward so that the optimal policy can be learned effectively. Different from the prior model-based work, which suffers from the scalability problem, our framework is easy to be deployed in large-scale industrial applications. The experimental evaluations demonstrate the effectiveness of our framework on large-scale real datasets.

A Multi-Agent Reinforcement Learning Method for Impression Allocation in Online Display Advertising

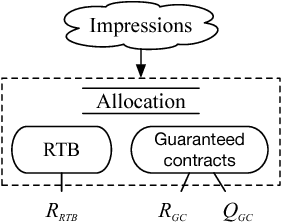
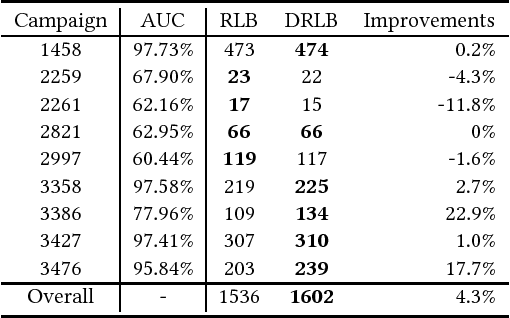
In online display advertising, guaranteed contracts and real-time bidding (RTB) are two major ways to sell impressions for a publisher. Despite the increasing popularity of RTB, there is still half of online display advertising revenue generated from guaranteed contracts. Therefore, simultaneously selling impressions through both guaranteed contracts and RTB is a straightforward choice for a publisher to maximize its yield. However, deriving the optimal strategy to allocate impressions is not a trivial task, especially when the environment is unstable in real-world applications. In this paper, we formulate the impression allocation problem as an auction problem where each contract can submit virtual bids for individual impressions. With this formulation, we derive the optimal impression allocation strategy by solving the optimal bidding functions for contracts. Since the bids from contracts are decided by the publisher, we propose a multi-agent reinforcement learning (MARL) approach to derive cooperative policies for the publisher to maximize its yield in an unstable environment. The proposed approach also resolves the common challenges in MARL such as input dimension explosion, reward credit assignment, and non-stationary environment. Experimental evaluations on large-scale real datasets demonstrate the effectiveness of our approach.