Revisiting semi-supervised training objectives for differentiable particle filters

Differentiable particle filters combine the flexibility of neural networks with the probabilistic nature of sequential Monte Carlo methods. However, traditional approaches rely on the availability of labelled data, i.e., the ground truth latent state information, which is often difficult to obtain in real-world applications. This paper compares the effectiveness of two semi-supervised training objectives for differentiable particle filters. We present results in two simulated environments where labelled data are scarce.

Normalising Flow-based Differentiable Particle Filters

Recently, there has been a surge of interest in incorporating neural networks into particle filters, e.g. differentiable particle filters, to perform joint sequential state estimation and model learning for non-linear non-Gaussian state-space models in complex environments. Existing differentiable particle filters are mostly constructed with vanilla neural networks that do not allow density estimation. As a result, they are either restricted to a bootstrap particle filtering framework or employ predefined distribution families (e.g. Gaussian distributions), limiting their performance in more complex real-world scenarios. In this paper we present a differentiable particle filtering framework that uses (conditional) normalising flows to build its dynamic model, proposal distribution, and measurement model. This not only enables valid probability densities but also allows the proposed method to adaptively learn these modules in a flexible way, without being restricted to predefined distribution families. We derive the theoretical properties of the proposed filters and evaluate the proposed normalising flow-based differentiable particle filters' performance through a series of numerical experiments.

Learning Differentiable Particle Filter on the Fly

Differentiable particle filters are an emerging class of sequential Bayesian inference techniques that use neural networks to construct components in state space models. Existing approaches are mostly based on offline supervised training strategies. This leads to the delay of the model deployment and the obtained filters are susceptible to distribution shift of test-time data. In this paper, we propose an online learning framework for differentiable particle filters so that model parameters can be updated as data arrive. The technical constraint is that there is no known ground truth state information in the online inference setting. We address this by adopting an unsupervised loss to construct the online model updating procedure, which involves a sequence of filtering operations for online maximum likelihood-based parameter estimation. We empirically evaluate the effectiveness of the proposed method, and compare it with supervised learning methods in simulation settings including a multivariate linear Gaussian state-space model and a simulated object tracking experiment.

Differentiable Bootstrap Particle Filters for Regime-Switching Models

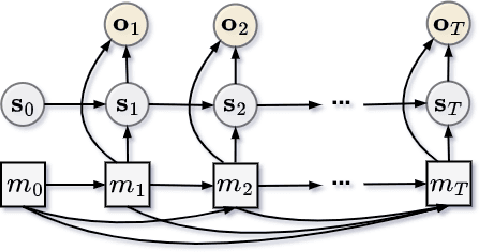
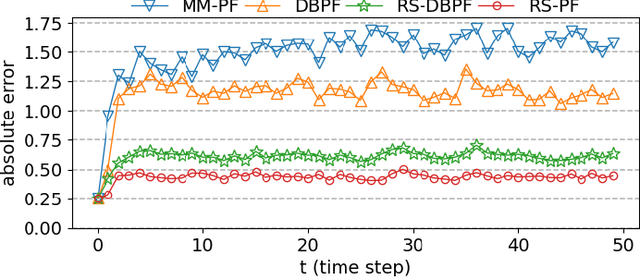
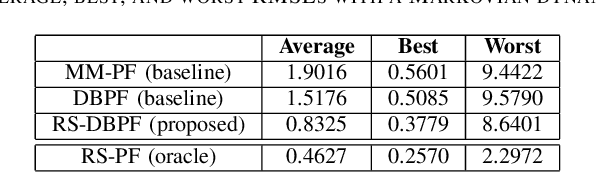
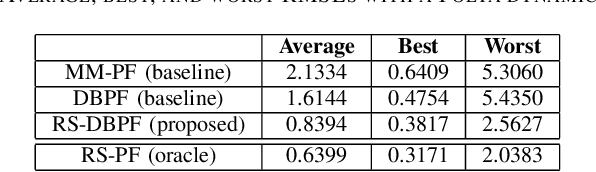
Differentiable particle filters are an emerging class of particle filtering methods that use neural networks to construct and learn parametric state-space models. In real-world applications, both the state dynamics and measurements can switch between a set of candidate models. For instance, in target tracking, vehicles can idle, move through traffic, or cruise on motorways, and measurements are collected in different geographical or weather conditions. This paper proposes a new differentiable particle filter for regime-switching state-space models. The method can learn a set of unknown candidate dynamic and measurement models and track the state posteriors. We evaluate the performance of the novel algorithm in relevant models, showing its great performance compared to other competitive algorithms.

An overview of differentiable particle filters for data-adaptive sequential Bayesian inference

By approximating posterior distributions with weighted samples, particle filters (PFs) provide an efficient mechanism for solving non-linear sequential state estimation problems. While the effectiveness of particle filters has been recognised in various applications, the performance of particle filters relies on the knowledge of dynamic models and measurement models, and the construction of effective proposal distributions. An emerging trend in designing particle filters is the differentiable particle filters (DPFs). By constructing particle filters' components through neural networks and optimising them by gradient descent, differentiable particle filters are a promising computational tool to perform inference for sequence data in complex high-dimensional tasks such as vision-based robot localisation. In this paper, we provide a review of recent advances in differentiable particle filters and their applications. We place special emphasis on different design choices of key components of differentiable particle filters, including dynamic models, measurement models, proposal distributions, optimisation objectives, and differentiable resampling techniques.

Batch-Ensemble Stochastic Neural Networks for Out-of-Distribution Detection

Out-of-distribution (OOD) detection has recently received much attention from the machine learning community due to its importance in deploying machine learning models in real-world applications. In this paper we propose an uncertainty quantification approach by modelling the distribution of features. We further incorporate an efficient ensemble mechanism, namely batch-ensemble, to construct the batch-ensemble stochastic neural networks (BE-SNNs) and overcome the feature collapse problem. We compare the performance of the proposed BE-SNNs with the other state-of-the-art approaches and show that BE-SNNs yield superior performance on several OOD benchmarks, such as the Two-Moons dataset, the FashionMNIST vs MNIST dataset, FashionMNIST vs NotMNIST dataset, and the CIFAR10 vs SVHN dataset.

Conditional Measurement Density Estimation in Sequential Monte Carlo via Normalizing Flow

Tuning of measurement models is challenging in real-world applications of sequential Monte Carlo methods. Recent advances in differentiable particle filters have led to various efforts to learn measurement models through neural networks. But existing approaches in the differentiable particle filter framework do not admit valid probability densities in constructing measurement models, leading to incorrect quantification of the measurement uncertainty given state information. We propose to learn expressive and valid probability densities in measurement models through conditional normalizing flows, to capture the complex likelihood of measurements given states. We show that the proposed approach leads to improved estimation performance and faster training convergence in a visual tracking experiment.

Differentiable Particle Filters through Conditional Normalizing Flow

Differentiable particle filters provide a flexible mechanism to adaptively train dynamic and measurement models by learning from observed data. However, most existing differentiable particle filters are within the bootstrap particle filtering framework and fail to incorporate the information from latest observations to construct better proposals. In this paper, we utilize conditional normalizing flows to construct proposal distributions for differentiable particle filters, enriching the distribution families that the proposal distributions can represent. In addition, normalizing flows are incorporated in the construction of the dynamic model, resulting in a more expressive dynamic model. We demonstrate the performance of the proposed conditional normalizing flow-based differentiable particle filters in a visual tracking task.

End-To-End Semi-supervised Learning for Differentiable Particle Filters

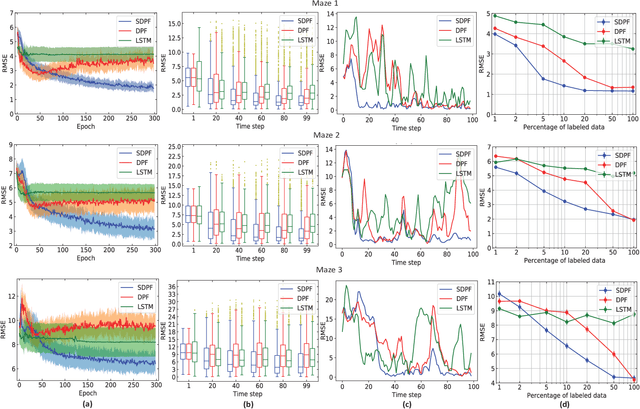
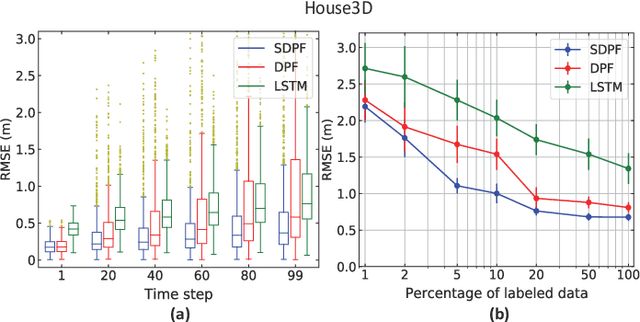
Recent advances in incorporating neural networks into particle filters provide the desired flexibility to apply particle filters in large-scale real-world applications. The dynamic and measurement models in this framework are learnable through the differentiable implementation of particle filters. Past efforts in optimising such models often require the knowledge of true states which can be expensive to obtain or even unavailable in practice. In this paper, in order to reduce the demand for annotated data, we present an end-to-end learning objective based upon the maximisation of a pseudo-likelihood function which can improve the estimation of states when large portion of true states are unknown. We assess performance of the proposed method in state estimation tasks in robotics with simulated and real-world datasets.

Augmented Sliced Wasserstein Distances

While theoretically appealing, the application of the Wasserstein distance to large-scale machine learning problems has been hampered by its prohibitive computational cost. The sliced Wasserstein distance and its variants improve the computational efficiency through random projection, yet they suffer from low projection efficiency because the majority of projections result in trivially small values. In this work, we propose a new family of distance metrics, called augmented sliced Wasserstein distances (ASWDs), constructed by first mapping samples to higher-dimensional hypersurfaces parameterized by neural networks. It is derived from a key observation that (random) linear projections of samples residing on these hypersurfaces would translate to much more flexible projections in the original sample space, so they can capture complex structures of the data distribution. We show that the hypersurfaces can be optimized by gradient ascent efficiently. We provide the condition under which the ASWD is a valid metric and show that this can be obtained by an injective neural network architecture. Numerical results demonstrate that the ASWD significantly outperforms other Wasserstein variants for both synthetic and real-world problems.