A Parallel Hybrid Action Space Reinforcement Learning Model for Real-world Adaptive Traffic Signal Control

Adaptive traffic signal control (ATSC) can effectively reduce vehicle travel times by dynamically adjusting signal timings but poses a critical challenge in real-world scenarios due to the complexity of real-time decision-making in dynamic and uncertain traffic conditions. The burgeoning field of intelligent transportation systems, bolstered by artificial intelligence techniques and extensive data availability, offers new prospects for the implementation of ATSC. In this study, we introduce a parallel hybrid action space reinforcement learning model (PH-DDPG) that optimizes traffic signal phase and duration of traffic signals simultaneously, eliminating the need for sequential decision-making seen in traditional two-stage models. Our model features a task-specific parallel hybrid action space tailored for adaptive traffic control, which directly outputs discrete phase selections and their associated continuous duration parameters concurrently, thereby inherently addressing dynamic traffic adaptation through unified parametric optimization. %Our model features a unique parallel hybrid action space that allows for the simultaneous output of each action and its optimal parameters, streamlining the decision-making process. Furthermore, to ascertain the robustness and effectiveness of this approach, we executed ablation studies focusing on the utilization of a random action parameter mask within the critic network, which decouples the parameter space for individual actions, facilitating the use of preferable parameters for each action. The results from these studies confirm the efficacy of this method, distinctly enhancing real-world applicability

Learning to optimize by multi-gradient for multi-objective optimization

The development of artificial intelligence (AI) for science has led to the emergence of learning-based research paradigms, necessitating a compelling reevaluation of the design of multi-objective optimization (MOO) methods. The new generation MOO methods should be rooted in automated learning rather than manual design. In this paper, we introduce a new automatic learning paradigm for optimizing MOO problems, and propose a multi-gradient learning to optimize (ML2O) method, which automatically learns a generator (or mappings) from multiple gradients to update directions. As a learning-based method, ML2O acquires knowledge of local landscapes by leveraging information from the current step and incorporates global experience extracted from historical iteration trajectory data. By introducing a new guarding mechanism, we propose a guarded multi-gradient learning to optimize (GML2O) method, and prove that the iterative sequence generated by GML2O converges to a Pareto critical point. The experimental results demonstrate that our learned optimizer outperforms hand-designed competitors on training multi-task learning (MTL) neural network.

A novel multiobjective evolutionary algorithm based on decomposition and multi-reference points strategy

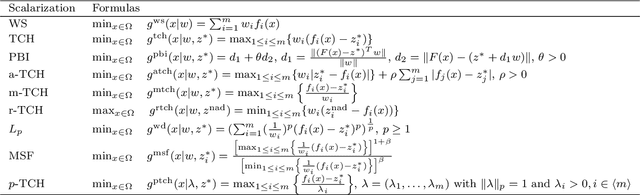
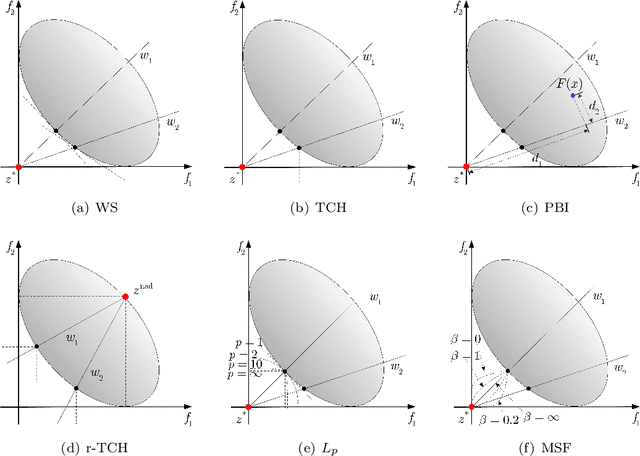
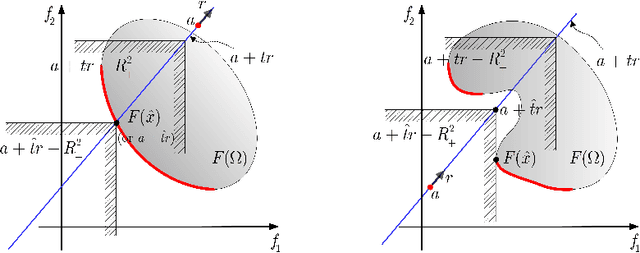
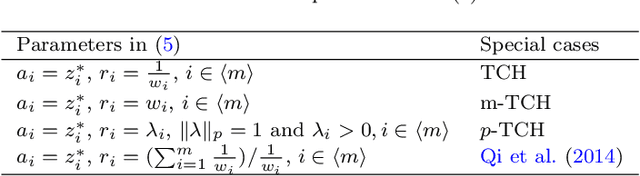
Many real-world optimization problems such as engineering design can be eventually modeled as the corresponding multiobjective optimization problems (MOPs) which must be solved to obtain approximate Pareto optimal fronts. Multiobjective evolutionary algorithm based on decomposition (MOEA/D) has been regarded as a significantly promising approach for solving MOPs. Recent studies have shown that MOEA/D with uniform weight vectors is well-suited to MOPs with regular Pareto optimal fronts, but its performance in terms of diversity usually deteriorates when solving MOPs with irregular Pareto optimal fronts. In this way, the solution set obtained by the algorithm can not provide more reasonable choices for decision makers. In order to efficiently overcome this drawback, we propose an improved MOEA/D algorithm by virtue of the well-known Pascoletti-Serafini scalarization method and a new strategy of multi-reference points. Specifically, this strategy consists of the setting and adaptation of reference points generated by the techniques of equidistant partition and projection. For performance assessment, the proposed algorithm is compared with existing four state-of-the-art multiobjective evolutionary algorithms on benchmark test problems with various types of Pareto optimal fronts. According to the experimental results, the proposed algorithm exhibits better diversity performance than that of the other compared algorithms. Finally, our algorithm is applied to two real-world MOPs in engineering optimization successfully.