A novel multiobjective evolutionary algorithm based on decomposition and multi-reference points strategy
Paper and Code
Nov 11, 2021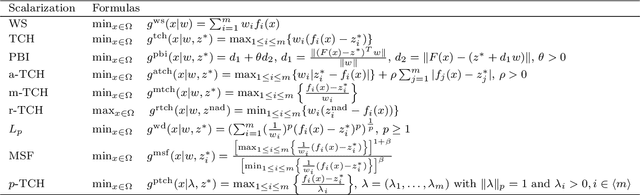
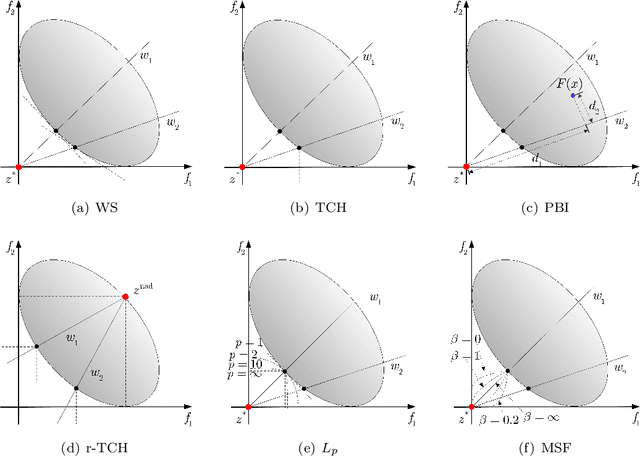
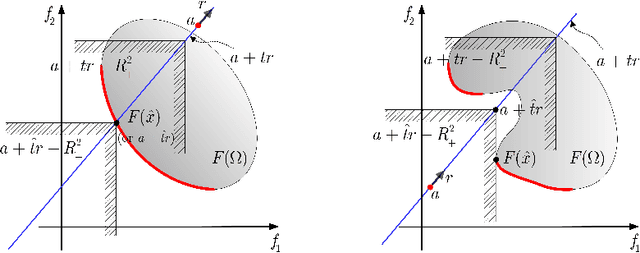
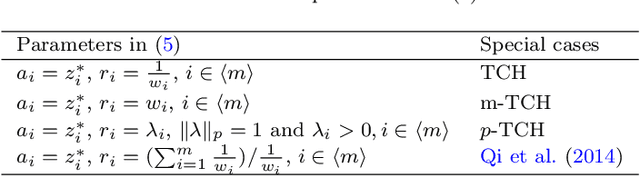
Many real-world optimization problems such as engineering design can be eventually modeled as the corresponding multiobjective optimization problems (MOPs) which must be solved to obtain approximate Pareto optimal fronts. Multiobjective evolutionary algorithm based on decomposition (MOEA/D) has been regarded as a significantly promising approach for solving MOPs. Recent studies have shown that MOEA/D with uniform weight vectors is well-suited to MOPs with regular Pareto optimal fronts, but its performance in terms of diversity usually deteriorates when solving MOPs with irregular Pareto optimal fronts. In this way, the solution set obtained by the algorithm can not provide more reasonable choices for decision makers. In order to efficiently overcome this drawback, we propose an improved MOEA/D algorithm by virtue of the well-known Pascoletti-Serafini scalarization method and a new strategy of multi-reference points. Specifically, this strategy consists of the setting and adaptation of reference points generated by the techniques of equidistant partition and projection. For performance assessment, the proposed algorithm is compared with existing four state-of-the-art multiobjective evolutionary algorithms on benchmark test problems with various types of Pareto optimal fronts. According to the experimental results, the proposed algorithm exhibits better diversity performance than that of the other compared algorithms. Finally, our algorithm is applied to two real-world MOPs in engineering optimization successfully.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge