Polynomial Convergence of Riemannian Diffusion Models

Diffusion models have demonstrated remarkable empirical success in the recent years and are considered one of the state-of-the-art generative models in modern AI. These models consist of a forward process, which gradually diffuses the data distribution to a noise distribution spanning the whole space, and a backward process, which inverts this transformation to recover the data distribution from noise. Most of the existing literature assumes that the underlying space is Euclidean. However, in many practical applications, the data are constrained to lie on a submanifold of Euclidean space. Addressing this setting, De Bortoli et al. (2022) introduced Riemannian diffusion models and proved that using an exponentially small step size yields a small sampling error in the Wasserstein distance, provided the data distribution is smooth and strictly positive, and the score estimate is $L_\infty$-accurate. In this paper, we greatly strengthen this theory by establishing that, under $L_2$-accurate score estimate, a {\em polynomially small stepsize} suffices to guarantee small sampling error in the total variation distance, without requiring smoothness or positivity of the data distribution. Our analysis only requires mild and standard curvature assumptions on the underlying manifold. The main ingredients in our analysis are Li-Yau estimate for the log-gradient of heat kernel, and Minakshisundaram-Pleijel parametrix expansion of the perturbed heat equation. Our approach opens the door to a sharper analysis of diffusion models on non-Euclidean spaces.

Agnostic Active Learning of Single Index Models with Linear Sample Complexity

We study active learning methods for single index models of the form $F({\mathbf x}) = f(\langle {\mathbf w}, {\mathbf x}\rangle)$, where $f:\mathbb{R} \to \mathbb{R}$ and ${\mathbf x,\mathbf w} \in \mathbb{R}^d$. In addition to their theoretical interest as simple examples of non-linear neural networks, single index models have received significant recent attention due to applications in scientific machine learning like surrogate modeling for partial differential equations (PDEs). Such applications require sample-efficient active learning methods that are robust to adversarial noise. I.e., that work even in the challenging agnostic learning setting. We provide two main results on agnostic active learning of single index models. First, when $f$ is known and Lipschitz, we show that $\tilde{O}(d)$ samples collected via {statistical leverage score sampling} are sufficient to learn a near-optimal single index model. Leverage score sampling is simple to implement, efficient, and already widely used for actively learning linear models. Our result requires no assumptions on the data distribution, is optimal up to log factors, and improves quadratically on a recent ${O}(d^{2})$ bound of \cite{gajjar2023active}. Second, we show that $\tilde{O}(d)$ samples suffice even in the more difficult setting when $f$ is \emph{unknown}. Our results leverage tools from high dimensional probability, including Dudley's inequality and dual Sudakov minoration, as well as a novel, distribution-aware discretization of the class of Lipschitz functions.

Provably Robust Score-Based Diffusion Posterior Sampling for Plug-and-Play Image Reconstruction

In a great number of tasks in science and engineering, the goal is to infer an unknown image from a small number of measurements collected from a known forward model describing certain sensing or imaging modality. Due to resource constraints, this task is often extremely ill-posed, which necessitates the adoption of expressive prior information to regularize the solution space. Score-based diffusion models, due to its impressive empirical success, have emerged as an appealing candidate of an expressive prior in image reconstruction. In order to accommodate diverse tasks at once, it is of great interest to develop efficient, consistent and robust algorithms that incorporate {\em unconditional} score functions of an image prior distribution in conjunction with flexible choices of forward models. This work develops an algorithmic framework for employing score-based diffusion models as an expressive data prior in general nonlinear inverse problems. Motivated by the plug-and-play framework in the imaging community, we introduce a diffusion plug-and-play method (\textsf{DPnP}) that alternatively calls two samplers, a proximal consistency sampler based solely on the likelihood function of the forward model, and a denoising diffusion sampler based solely on the score functions of the image prior. The key insight is that denoising under white Gaussian noise can be solved {\em rigorously} via both stochastic (i.e., DDPM-type) and deterministic (i.e., DDIM-type) samplers using the unconditional score functions. We establish both asymptotic and non-asymptotic performance guarantees of \textsf{DPnP}, and provide numerical experiments to illustrate its promise in solving both linear and nonlinear image reconstruction tasks. To the best of our knowledge, \textsf{DPnP} is the first provably-robust posterior sampling method for nonlinear inverse problems using unconditional diffusion priors.

Provably Accelerating Ill-Conditioned Low-rank Estimation via Scaled Gradient Descent, Even with Overparameterization

Many problems encountered in science and engineering can be formulated as estimating a low-rank object (e.g., matrices and tensors) from incomplete, and possibly corrupted, linear measurements. Through the lens of matrix and tensor factorization, one of the most popular approaches is to employ simple iterative algorithms such as gradient descent (GD) to recover the low-rank factors directly, which allow for small memory and computation footprints. However, the convergence rate of GD depends linearly, and sometimes even quadratically, on the condition number of the low-rank object, and therefore, GD slows down painstakingly when the problem is ill-conditioned. This chapter introduces a new algorithmic approach, dubbed scaled gradient descent (ScaledGD), that provably converges linearly at a constant rate independent of the condition number of the low-rank object, while maintaining the low per-iteration cost of gradient descent for a variety of tasks including sensing, robust principal component analysis and completion. In addition, ScaledGD continues to admit fast global convergence to the minimax-optimal solution, again almost independent of the condition number, from a small random initialization when the rank is over-specified in the presence of Gaussian noise. In total, ScaledGD highlights the power of appropriate preconditioning in accelerating nonconvex statistical estimation, where the iteration-varying preconditioners promote desirable invariance properties of the trajectory with respect to the symmetry in low-rank factorization without hurting generalization.

The Power of Preconditioning in Overparameterized Low-Rank Matrix Sensing

We propose $\textsf{ScaledGD($\lambda$)}$, a preconditioned gradient descent method to tackle the low-rank matrix sensing problem when the true rank is unknown, and when the matrix is possibly ill-conditioned. Using overparametrized factor representations, $\textsf{ScaledGD($\lambda$)}$ starts from a small random initialization, and proceeds by gradient descent with a specific form of damped preconditioning to combat bad curvatures induced by overparameterization and ill-conditioning. At the expense of light computational overhead incurred by preconditioners, $\textsf{ScaledGD($\lambda$)}$ is remarkably robust to ill-conditioning compared to vanilla gradient descent ($\textsf{GD}$) even with overprameterization. Specifically, we show that, under the Gaussian design, $\textsf{ScaledGD($\lambda$)}$ converges to the true low-rank matrix at a constant linear rate after a small number of iterations that scales only logarithmically with respect to the condition number and the problem dimension. This significantly improves over the convergence rate of vanilla $\textsf{GD}$ which suffers from a polynomial dependency on the condition number. Our work provides evidence on the power of preconditioning in accelerating the convergence without hurting generalization in overparameterized learning.

Phase Transitions in Frequency Agile Radar Using Compressed Sensing

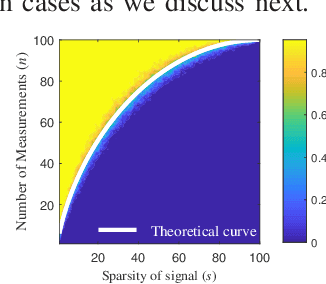
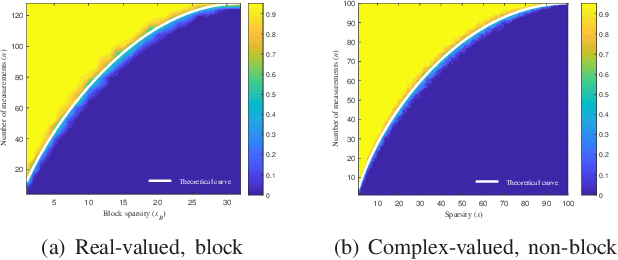
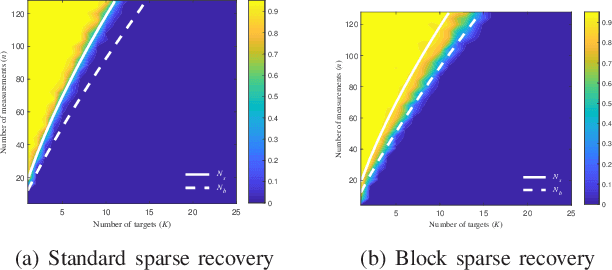
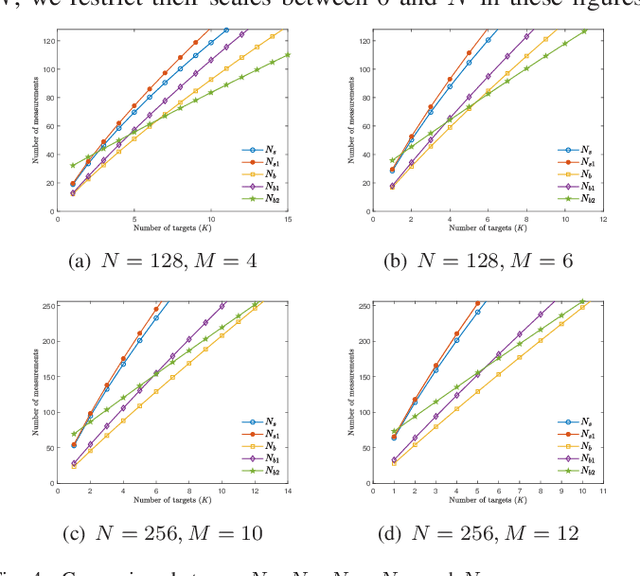
FAR has improved anti-jamming performance over traditional pulse-Doppler radars under complex electromagnetic circumstances. To reconstruct the range-Doppler information in FAR, many compressed sensing (CS) methods including standard and block sparse recovery have been applied. In this paper, we study phase transitions of range-Doppler recovery in FAR using CS. In particular, we derive closed-form phase transition curves associated with block sparse recovery and complex Gaussian matrices, based on prior results of standard sparse recovery under real Gaussian matrices. We further approximate the obtained curves with elementary functions of radar and target parameters, facilitating practical applications of these curves. Our results indicate that block sparse recovery outperforms the standard counterpart when targets occupy more than one range cell, which are often referred to as extended targets. Simulations validate the availability of these curves and their approximations in FAR, which benefit the design of the radar parameters.