How Does the Lagrangian Guide Safe Reinforcement Learning through Diffusion Models?

Diffusion policy sampling enables reinforcement learning (RL) to represent multimodal action distributions beyond suboptimal unimodal Gaussian policies. However, existing diffusion-based RL methods primarily focus on offline settings for reward maximization, with limited consideration of safety in online settings. To address this gap, we propose Augmented Lagrangian-Guided Diffusion (ALGD), a novel algorithm for off-policy safe RL. By revisiting optimization theory and energy-based model, we show that the instability of primal-dual methods arises from the non-convex Lagrangian landscape. In diffusion-based safe RL, the Lagrangian can be interpreted as an energy function guiding the denoising dynamics. Counterintuitively, direct usage destabilizes both policy generation and training. ALGD resolves this issue by introducing an augmented Lagrangian that locally convexifies the energy landscape, yielding a stabilized policy generation and training process without altering the distribution of the optimal policy. Theoretical analysis and extensive experiments demonstrate that ALGD is both theoretically grounded and empirically effective, achieving strong and stable performance across diverse environments.

On Stability and Robustness of Diffusion Posterior Sampling for Bayesian Inverse Problems

Diffusion models have recently emerged as powerful learned priors for Bayesian inverse problems (BIPs). Diffusion-based solvers rely on a presumed likelihood for the observations in BIPs to guide the generation process. However, the link between likelihood and recovery quality for BIPs is unclear in previous works. We bridge this gap by characterizing the posterior approximation error and proving the \emph{stability} of the diffusion-based solvers. Meanwhile, an immediate result of our findings on stability demonstrates the lack of robustness in diffusion-based solvers, which remains unexplored. This can degrade performance when the presumed likelihood mismatches the unknown true data generation processes. To address this issue, we propose a simple yet effective solution, \emph{robust diffusion posterior sampling}, which is provably \emph{robust} and compatible with existing gradient-based posterior samplers. Empirical results on scientific inverse problems and natural image tasks validate the effectiveness and robustness of our method, showing consistent performance improvements under challenging likelihood misspecifications.

Planning with Language and Generative Models: Toward General Reward-Guided Wireless Network Design

Intelligent access point (AP) deployment remains challenging in next-generation wireless networks due to complex indoor geometries and signal propagation. We firstly benchmark general-purpose large language models (LLMs) as agentic optimizers for AP planning and find that, despite strong wireless domain knowledge, their dependence on external verifiers results in high computational costs and limited scalability. Motivated by these limitations, we study generative inference models guided by a unified reward function capturing core AP deployment objectives across diverse floorplans. We show that diffusion samplers consistently outperform alternative generative approaches. The diffusion process progressively improves sampling by smoothing and sharpening the reward landscape, rather than relying on iterative refinement, which is effective for non-convex and fragmented objectives. Finally, we introduce a large-scale real-world dataset for indoor AP deployment, requiring over $50k$ CPU hours to train general reward functions, and evaluate in- and out-of-distribution generalization and robustness. Our results suggest that diffusion-based generative inference with a unified reward function provides a scalable and domain-agnostic foundation for indoor AP deployment planning.

Fast-Forward Lattice Boltzmann: Learning Kinetic Behaviour with Physics-Informed Neural Operators

The lattice Boltzmann equation (LBE), rooted in kinetic theory, provides a powerful framework for capturing complex flow behaviour by describing the evolution of single-particle distribution functions (PDFs). Despite its success, solving the LBE numerically remains computationally intensive due to strict time-step restrictions imposed by collision kernels. Here, we introduce a physics-informed neural operator framework for the LBE that enables prediction over large time horizons without step-by-step integration, effectively bypassing the need to explicitly solve the collision kernel. We incorporate intrinsic moment-matching constraints of the LBE, along with global equivariance of the full distribution field, enabling the model to capture the complex dynamics of the underlying kinetic system. Our framework is discretization-invariant, enabling models trained on coarse lattices to generalise to finer ones (kinetic super-resolution). In addition, it is agnostic to the specific form of the underlying collision model, which makes it naturally applicable across different kinetic datasets regardless of the governing dynamics. Our results demonstrate robustness across complex flow scenarios, including von Karman vortex shedding, ligament breakup, and bubble adhesion. This establishes a new data-driven pathway for modelling kinetic systems.

AlphaZero-Edu: Making AlphaZero Accessible to Everyone

Recent years have witnessed significant progress in reinforcement learning, especially with Zero-like paradigms, which have greatly boosted the generalization and reasoning abilities of large-scale language models. Nevertheless, existing frameworks are often plagued by high implementation complexity and poor reproducibility. To tackle these challenges, we present AlphaZero-Edu, a lightweight, education-focused implementation built upon the mathematical framework of AlphaZero. It boasts a modular architecture that disentangles key components, enabling transparent visualization of the algorithmic processes. Additionally, it is optimized for resource-efficient training on a single NVIDIA RTX 3090 GPU and features highly parallelized self-play data generation, achieving a 3.2-fold speedup with 8 processes. In Gomoku matches, the framework has demonstrated exceptional performance, achieving a consistently high win rate against human opponents. AlphaZero-Edu has been open-sourced at https://github.com/StarLight1212/AlphaZero_Edu, providing an accessible and practical benchmark for both academic research and industrial applications.

KEEC: Embed to Control on An Equivariant Geometry

This paper investigates how representation learning can enable optimal control in unknown and complex dynamics, such as chaotic and non-linear systems, without relying on prior domain knowledge of the dynamics. The core idea is to establish an equivariant geometry that is diffeomorphic to the manifold defined by a dynamical system and to perform optimal control within this corresponding geometry, which is a non-trivial task. To address this challenge, Koopman Embed to Equivariant Control (KEEC) is introduced for model learning and control. Inspired by Lie theory, KEEC begins by learning a non-linear dynamical system defined on a manifold and embedding trajectories into a Lie group. Subsequently, KEEC formulates an equivariant value function equation in reinforcement learning on the equivariant geometry, ensuring an invariant effect as the value function on the original manifold. By deriving analytical-form optimal actions on the equivariant value function, KEEC theoretically achieves quadratic convergence for the optimal equivariant value function by leveraging the differential information on the equivariant geometry. The effectiveness of KEEC is demonstrated in challenging dynamical systems, including chaotic ones like Lorenz-63. Notably, our findings indicate that isometric and isomorphic loss functions, ensuring the compactness and smoothness of geometry, outperform loss functions without these properties.

Safe Reinforcement Learning in Tensor Reproducing Kernel Hilbert Space

This paper delves into the problem of safe reinforcement learning (RL) in a partially observable environment with the aim of achieving safe-reachability objectives. In traditional partially observable Markov decision processes (POMDP), ensuring safety typically involves estimating the belief in latent states. However, accurately estimating an optimal Bayesian filter in POMDP to infer latent states from observations in a continuous state space poses a significant challenge, largely due to the intractable likelihood. To tackle this issue, we propose a stochastic model-based approach that guarantees RL safety almost surely in the face of unknown system dynamics and partial observation environments. We leveraged the Predictive State Representation (PSR) and Reproducing Kernel Hilbert Space (RKHS) to represent future multi-step observations analytically, and the results in this context are provable. Furthermore, we derived essential operators from the kernel Bayes' rule, enabling the recursive estimation of future observations using various operators. Under the assumption of \textit{undercompleness}, a polynomial sample complexity is established for the RL algorithm for the infinite size of observation and action spaces, ensuring an $\epsilon-$suboptimal safe policy guarantee.

Times Series Forecasting for Urban Building Energy Consumption Based on Graph Convolutional Network

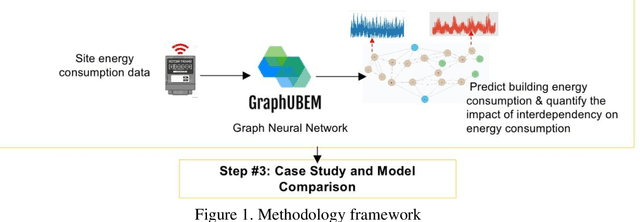
The world is increasingly urbanizing and the building industry accounts for more than 40% of energy consumption in the United States. To improve urban sustainability, many cities adopt ambitious energy-saving strategies through retrofitting existing buildings and constructing new communities. In this situation, an accurate urban building energy model (UBEM) is the foundation to support the design of energy-efficient communities. However, current UBEM are limited in their abilities to capture the inter-building interdependency due to their dynamic and non-linear characteristics. Those models either ignored or oversimplified these building interdependencies, which can substantially affect the accuracy of urban energy modeling. To fill the research gap, this study proposes a novel data-driven UBEM synthesizing the solar-based building interdependency and spatial-temporal graph convolutional network (ST-GCN) algorithm. Especially, we took a university campus located in downtown Atlanta as an example to predict the hourly energy consumption. Furthermore, we tested the feasibility of the proposed model by comparing the performance of the ST-GCN model with other common time-series machine learning models. The results indicate that the ST-GCN model overall outperforms all others. In addition, the physical knowledge embedded in the model is well interpreted. After discussion, it is found that data-driven models integrated engineering or physical knowledge can significantly improve the urban building energy simulation.