Spectral Subspace Clustering for Attributed Graphs

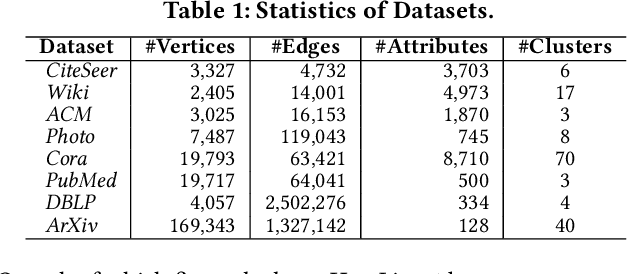
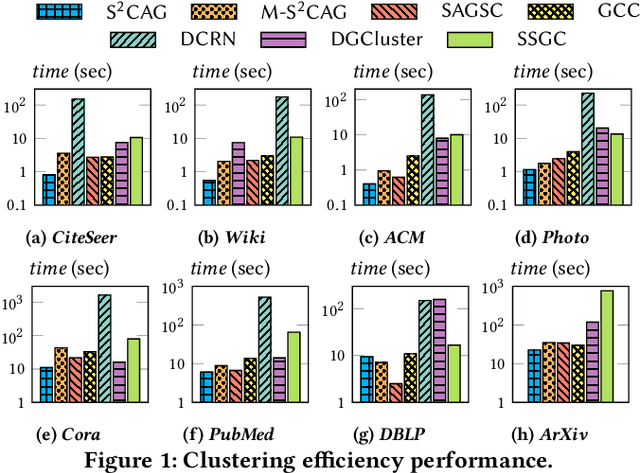
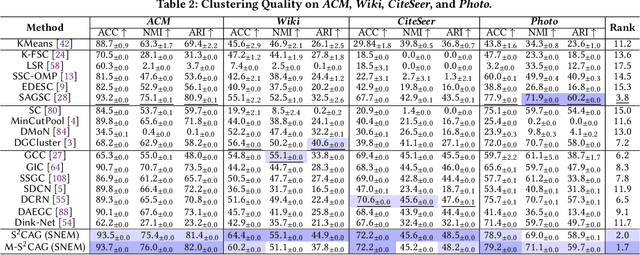
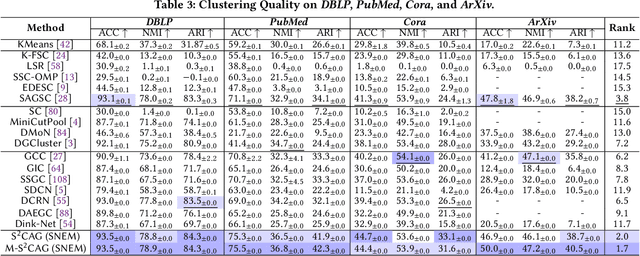
Subspace clustering seeks to identify subspaces that segment a set of n data points into k (k<<n) groups, which has emerged as a powerful tool for analyzing data from various domains, especially images and videos. Recently, several studies have demonstrated the great potential of subspace clustering models for partitioning vertices in attributed graphs, referred to as SCAG. However, these works either demand significant computational overhead for constructing the nxn self-expressive matrix, or fail to incorporate graph topology and attribute data into the subspace clustering framework effectively, and thus, compromise result quality. Motivated by this, this paper presents two effective and efficient algorithms, S2CAG and M-S2CAG, for SCAG computation. Particularly, S2CAG obtains superb performance through three major contributions. First, we formulate a new objective function for SCAG with a refined representation model for vertices and two non-trivial constraints. On top of that, an efficient linear-time optimization solver is developed based on our theoretically grounded problem transformation and well-thought-out adaptive strategy. We then conduct an in-depth analysis to disclose the theoretical connection of S2CAG to conductance minimization, which further inspires the design of M-S2CAG that maximizes the modularity. Our extensive experiments, comparing S2CAG and M-S2CAG against 17 competitors over 8 benchmark datasets, exhibit that our solutions outperform all baselines in terms of clustering quality measured against the ground truth while delivering high efficiency

Efficient Topology-aware Data Augmentation for High-Degree Graph Neural Networks

In recent years, graph neural networks (GNNs) have emerged as a potent tool for learning on graph-structured data and won fruitful successes in varied fields. The majority of GNNs follow the message-passing paradigm, where representations of each node are learned by recursively aggregating features of its neighbors. However, this mechanism brings severe over-smoothing and efficiency issues over high-degree graphs (HDGs), wherein most nodes have dozens (or even hundreds) of neighbors, such as social networks, transaction graphs, power grids, etc. Additionally, such graphs usually encompass rich and complex structure semantics, which are hard to capture merely by feature aggregations in GNNs. Motivated by the above limitations, we propose TADA, an efficient and effective front-mounted data augmentation framework for GNNs on HDGs. Under the hood, TADA includes two key modules: (i) feature expansion with structure embeddings, and (ii) topology- and attribute-aware graph sparsification. The former obtains augmented node features and enhanced model capacity by encoding the graph structure into high-quality structure embeddings with our highly-efficient sketching method. Further, by exploiting task-relevant features extracted from graph structures and attributes, the second module enables the accurate identification and reduction of numerous redundant/noisy edges from the input graph, thereby alleviating over-smoothing and facilitating faster feature aggregations over HDGs. Empirically, TADA considerably improves the predictive performance of mainstream GNN models on 8 real homophilic/heterophilic HDGs in terms of node classification, while achieving efficient training and inference processes.

Effective Clustering on Large Attributed Bipartite Graphs

Attributed bipartite graphs (ABGs) are an expressive data model for describing the interactions between two sets of heterogeneous nodes that are associated with rich attributes, such as customer-product purchase networks and author-paper authorship graphs. Partitioning the target node set in such graphs into k disjoint clusters (referred to as k-ABGC) finds widespread use in various domains, including social network analysis, recommendation systems, information retrieval, and bioinformatics. However, the majority of existing solutions towards k-ABGC either overlook attribute information or fail to capture bipartite graph structures accurately, engendering severely compromised result quality. The severity of these issues is accentuated in real ABGs, which often encompass millions of nodes and a sheer volume of attribute data, rendering effective k-ABGC over such graphs highly challenging. In this paper, we propose TPO, an effective and efficient approach to k-ABGC that achieves superb clustering performance on multiple real datasets. TPO obtains high clustering quality through two major contributions: (i) a novel formulation and transformation of the k-ABGC problem based on multi-scale attribute affinity specialized for capturing attribute affinities between nodes with the consideration of their multi-hop connections in ABGs, and (ii) a highly efficient solver that includes a suite of carefully-crafted optimizations for sidestepping explicit affinity matrix construction and facilitating faster convergence. Extensive experiments, comparing TPO against 19 baselines over 5 real ABGs, showcase the superior clustering quality of TPO measured against ground-truth labels. Moreover, compared to the state of the arts, TPO is often more than 40x faster over both small and large ABGs.