Spectral Subspace Clustering for Attributed Graphs
Paper and Code
Nov 17, 2024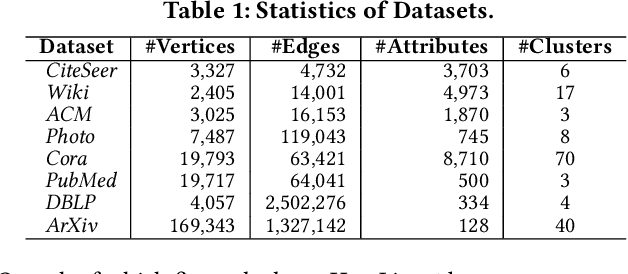
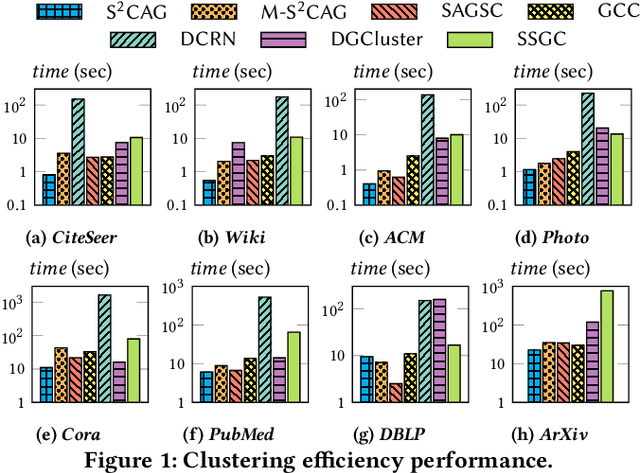
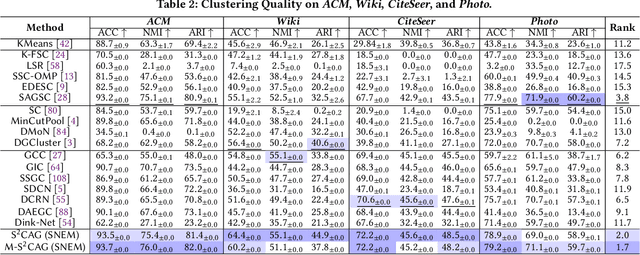
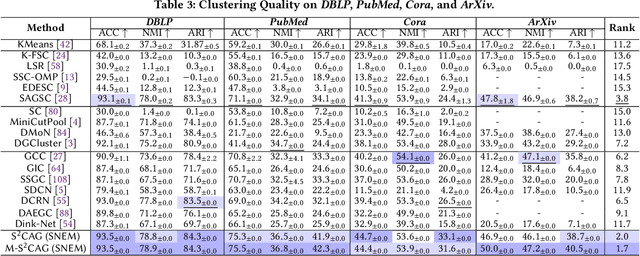
Subspace clustering seeks to identify subspaces that segment a set of n data points into k (k<<n) groups, which has emerged as a powerful tool for analyzing data from various domains, especially images and videos. Recently, several studies have demonstrated the great potential of subspace clustering models for partitioning vertices in attributed graphs, referred to as SCAG. However, these works either demand significant computational overhead for constructing the nxn self-expressive matrix, or fail to incorporate graph topology and attribute data into the subspace clustering framework effectively, and thus, compromise result quality. Motivated by this, this paper presents two effective and efficient algorithms, S2CAG and M-S2CAG, for SCAG computation. Particularly, S2CAG obtains superb performance through three major contributions. First, we formulate a new objective function for SCAG with a refined representation model for vertices and two non-trivial constraints. On top of that, an efficient linear-time optimization solver is developed based on our theoretically grounded problem transformation and well-thought-out adaptive strategy. We then conduct an in-depth analysis to disclose the theoretical connection of S2CAG to conductance minimization, which further inspires the design of M-S2CAG that maximizes the modularity. Our extensive experiments, comparing S2CAG and M-S2CAG against 17 competitors over 8 benchmark datasets, exhibit that our solutions outperform all baselines in terms of clustering quality measured against the ground truth while delivering high efficiency
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge