DNA-SE: Towards Deep Neural-Nets Assisted Semiparametric Estimation

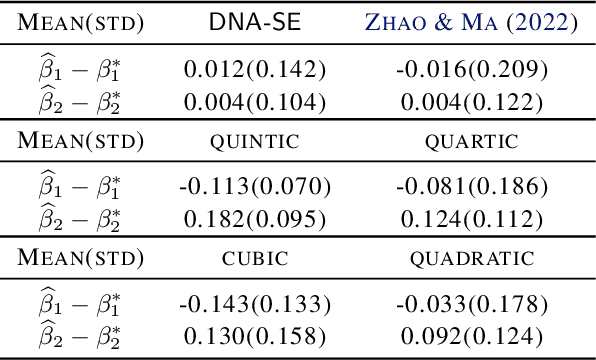
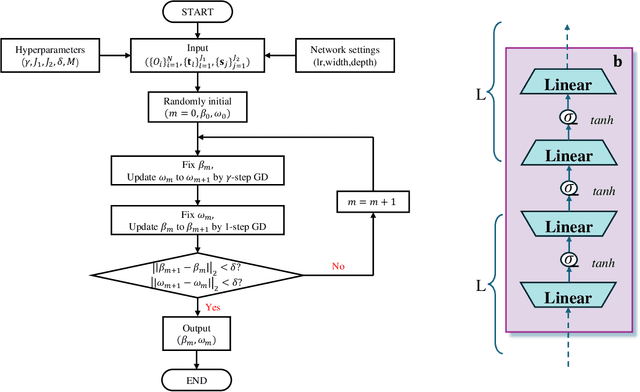
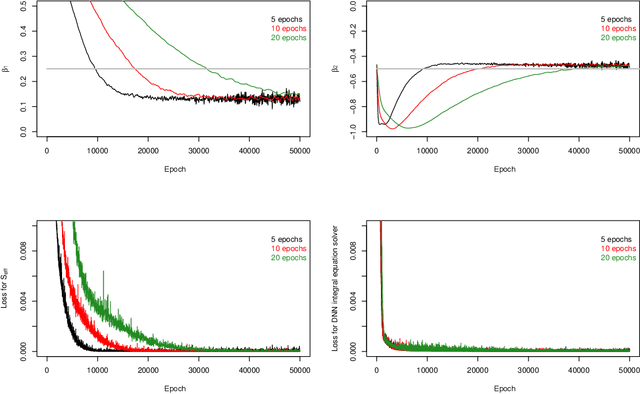
Semiparametric statistics play a pivotal role in a wide range of domains, including but not limited to missing data, causal inference, and transfer learning, to name a few. In many settings, semiparametric theory leads to (nearly) statistically optimal procedures that yet involve numerically solving Fredholm integral equations of the second kind. Traditional numerical methods, such as polynomial or spline approximations, are difficult to scale to multi-dimensional problems. Alternatively, statisticians may choose to approximate the original integral equations by ones with closed-form solutions, resulting in computationally more efficient, but statistically suboptimal or even incorrect procedures. To bridge this gap, we propose a novel framework by formulating the semiparametric estimation problem as a bi-level optimization problem; and then we develop a scalable algorithm called Deep Neural-Nets Assisted Semiparametric Estimation (DNA-SE) by leveraging the universal approximation property of Deep Neural-Nets (DNN) to streamline semiparametric procedures. Through extensive numerical experiments and a real data analysis, we demonstrate the numerical and statistical advantages of $\dnase$ over traditional methods. To the best of our knowledge, we are the first to bring DNN into semiparametric statistics as a numerical solver of integral equations in our proposed general framework.

Subspace Decomposition based DNN algorithm for elliptic type multi-scale PDEs

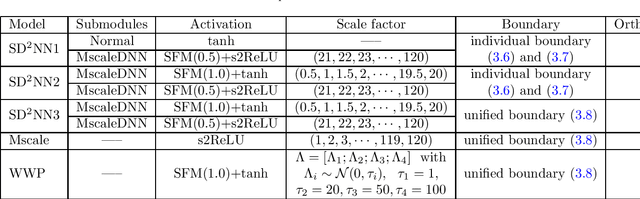
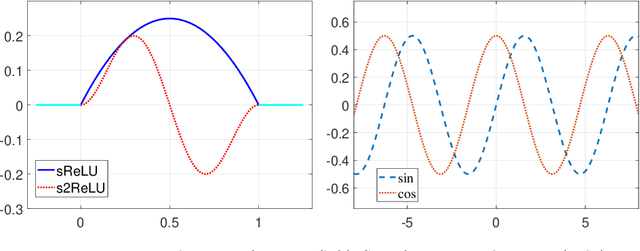
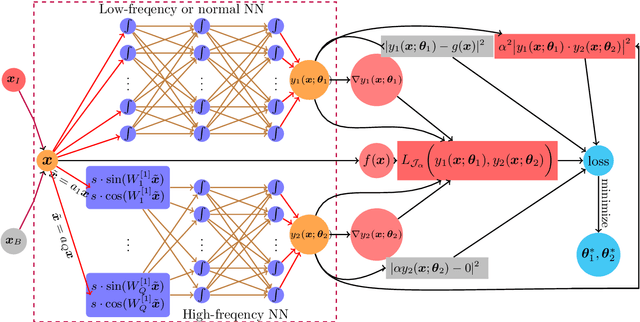
While deep learning algorithms demonstrate a great potential in scientific computing, its application to multi-scale problems remains to be a big challenge. This is manifested by the "frequency principle" that neural networks tend to learn low frequency components first. Novel architectures such as multi-scale deep neural network (MscaleDNN) were proposed to alleviate this problem to some extent. In this paper, we construct a subspace decomposition based DNN (dubbed SD$^2$NN) architecture for a class of multi-scale problems by combining traditional numerical analysis ideas and MscaleDNN algorithms. The proposed architecture includes one low frequency normal DNN submodule, and one (or a few) high frequency MscaleDNN submodule(s), which are designed to capture the smooth part and the oscillatory part of the multi-scale solutions, respectively. In addition, a novel trigonometric activation function is incorporated in the SD$^2$NN model. We demonstrate the performance of the SD$^2$NN architecture through several benchmark multi-scale problems in regular or irregular geometric domains. Numerical results show that the SD$^2$NN model is superior to existing models such as MscaleDNN.

Multi-scale Receptive Fields Graph Attention Network for Point Cloud Classification

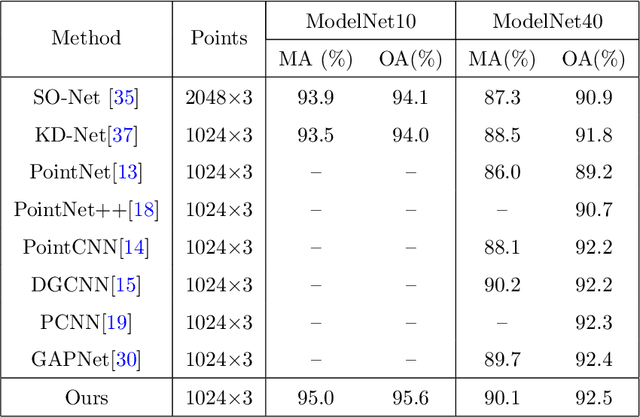
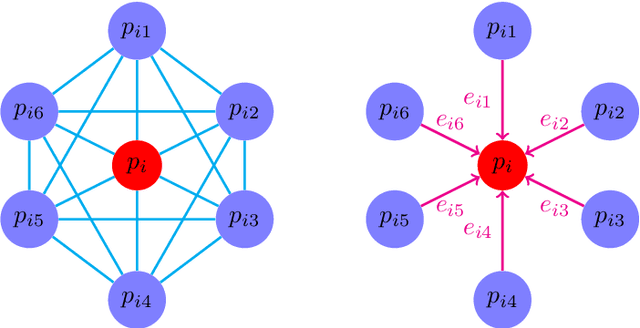
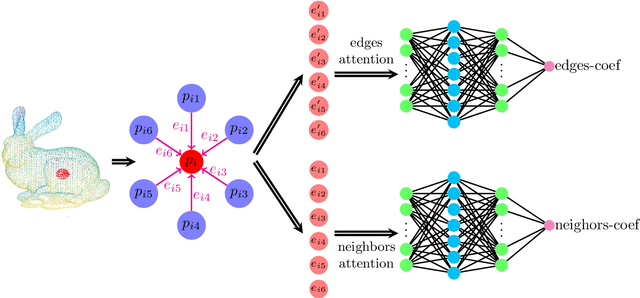
Understanding the implication of point cloud is still challenging to achieve the goal of classification or segmentation due to the irregular and sparse structure of point cloud. As we have known, PointNet architecture as a ground-breaking work for point cloud which can learn efficiently shape features directly on unordered 3D point cloud and have achieved favorable performance. However, this model fail to consider the fine-grained semantic information of local structure for point cloud. Afterwards, many valuable works are proposed to enhance the performance of PointNet by means of semantic features of local patch for point cloud. In this paper, a multi-scale receptive fields graph attention network (named after MRFGAT) for point cloud classification is proposed. By focusing on the local fine features of point cloud and applying multi attention modules based on channel affinity, the learned feature map for our network can well capture the abundant features information of point cloud. The proposed MRFGAT architecture is tested on ModelNet10 and ModelNet40 datasets, and results show it achieves state-of-the-art performance in shape classification tasks.