Subspace Decomposition based DNN algorithm for elliptic type multi-scale PDEs
Paper and Code
Dec 16, 2021
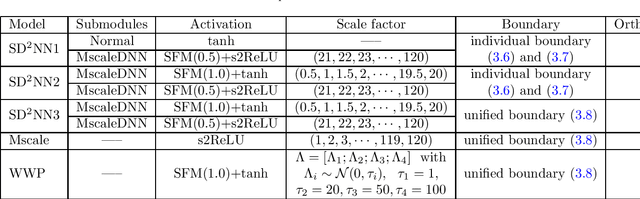
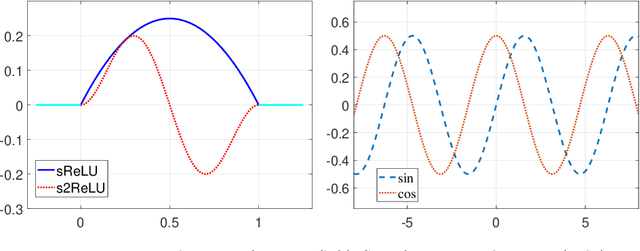
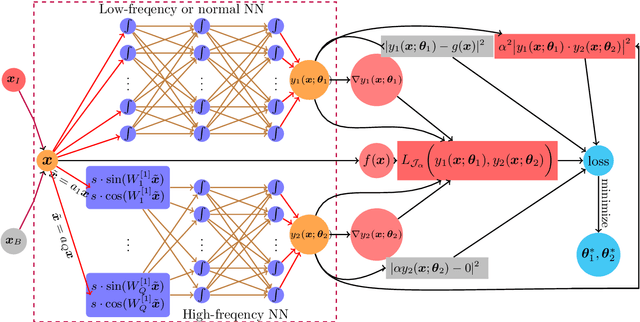
While deep learning algorithms demonstrate a great potential in scientific computing, its application to multi-scale problems remains to be a big challenge. This is manifested by the "frequency principle" that neural networks tend to learn low frequency components first. Novel architectures such as multi-scale deep neural network (MscaleDNN) were proposed to alleviate this problem to some extent. In this paper, we construct a subspace decomposition based DNN (dubbed SD$^2$NN) architecture for a class of multi-scale problems by combining traditional numerical analysis ideas and MscaleDNN algorithms. The proposed architecture includes one low frequency normal DNN submodule, and one (or a few) high frequency MscaleDNN submodule(s), which are designed to capture the smooth part and the oscillatory part of the multi-scale solutions, respectively. In addition, a novel trigonometric activation function is incorporated in the SD$^2$NN model. We demonstrate the performance of the SD$^2$NN architecture through several benchmark multi-scale problems in regular or irregular geometric domains. Numerical results show that the SD$^2$NN model is superior to existing models such as MscaleDNN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge