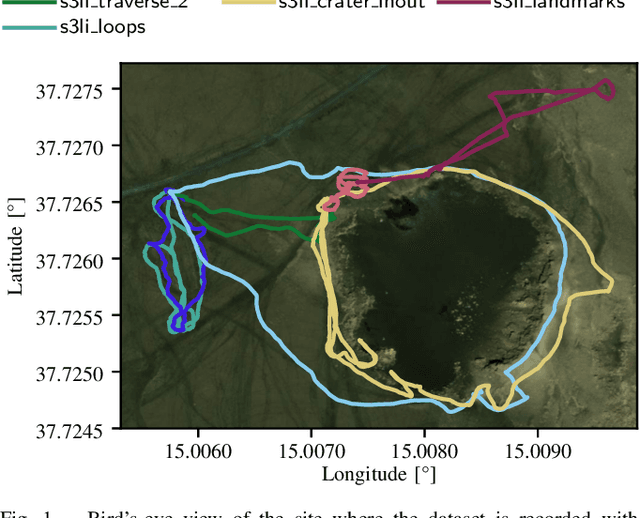
Challenges of SLAM in extremely unstructured environments: the DLR Planetary Stereo, Solid-State LiDAR, Inertial Dataset

We present the DLR Planetary Stereo, Solid-State LiDAR, Inertial (S3LI) dataset, recorded on Mt. Etna, Sicily, an environment analogous to the Moon and Mars, using a hand-held sensor suite with attributes suitable for implementation on a space-like mobile rover. The environment is characterized by challenging conditions regarding both the visual and structural appearance: severe visual aliasing poses significant limitations to the ability of visual SLAM systems to perform place recognition, while the absence of outstanding structural details, joined with the limited Field-of-View of the utilized Solid-State LiDAR sensor, challenges traditional LiDAR SLAM for the task of pose estimation using point clouds alone. With this data, that covers more than 4 kilometers of travel on soft volcanic slopes, we aim to: 1) provide a tool to expose limitations of state-of-the-art SLAM systems with respect to environments, which are not present in widely available datasets and 2) motivate the development of novel localization and mapping approaches, that rely efficiently on the complementary capabilities of the two sensors. The dataset is accessible at the following url: https://rmc.dlr.de/s3li_dataset

Towards Robust Monocular Visual Odometry for Flying Robots on Planetary Missions

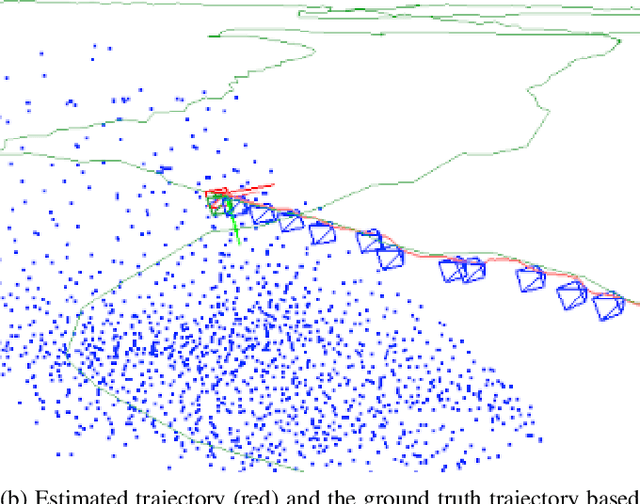
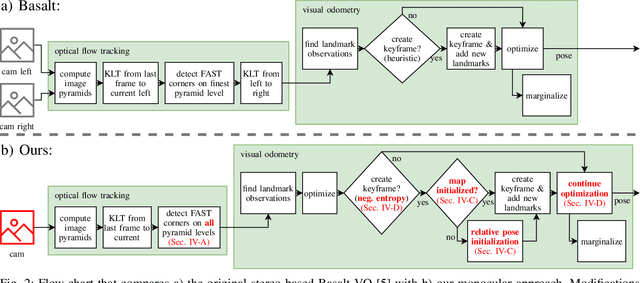
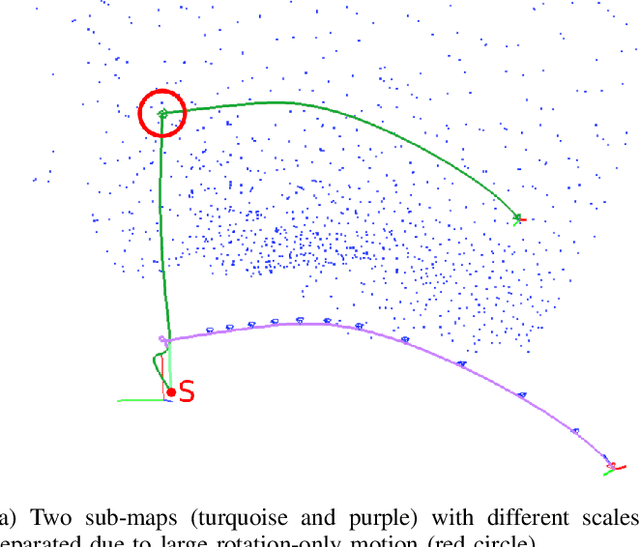
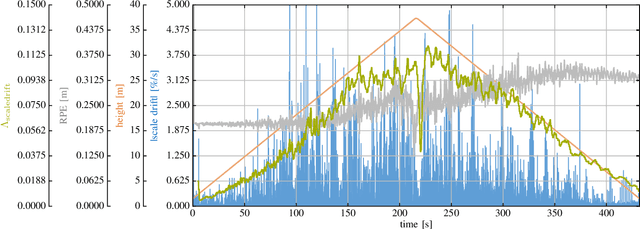
In the future, extraterrestrial expeditions will not only be conducted by rovers but also by flying robots. The technical demonstration drone Ingenuity, that just landed on Mars, will mark the beginning of a new era of exploration unhindered by terrain traversability. Robust self-localization is crucial for that. Cameras that are lightweight, cheap and information-rich sensors are already used to estimate the ego-motion of vehicles. However, methods proven to work in man-made environments cannot simply be deployed on other planets. The highly repetitive textures present in the wastelands of Mars pose a huge challenge to descriptor matching based approaches. In this paper, we present an advanced robust monocular odometry algorithm that uses efficient optical flow tracking to obtain feature correspondences between images and a refined keyframe selection criterion. In contrast to most other approaches, our framework can also handle rotation-only motions that are particularly challenging for monocular odometry systems. Furthermore, we present a novel approach to estimate the current risk of scale drift based on a principal component analysis of the relative translation information matrix. This way we obtain an implicit measure of uncertainty. We evaluate the validity of our approach on all sequences of a challenging real-world dataset captured in a Mars-like environment and show that it outperforms state-of-the-art approaches.

Multi-Modal Loop Closing in Unstructured Planetary Environments with Visually Enriched Submaps

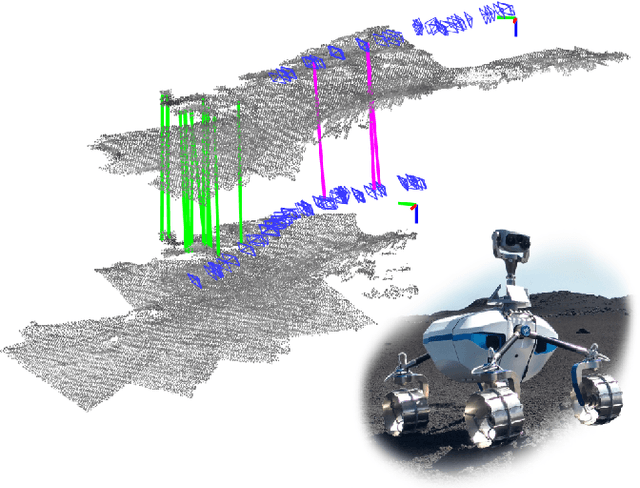
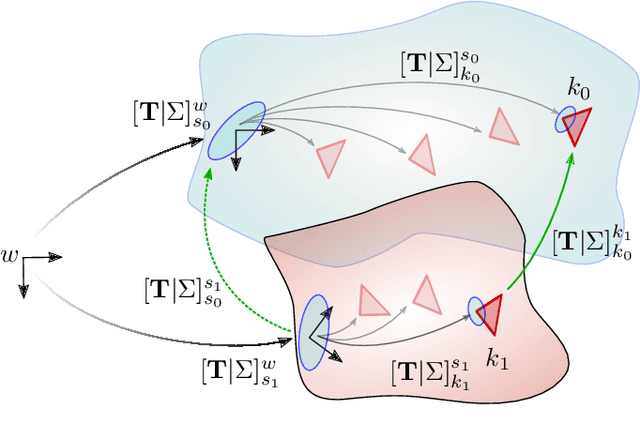
Future planetary missions will rely on rovers that can autonomously explore and navigate in unstructured environments. An essential element is the ability to recognize places that were already visited or mapped. In this work we leverage the ability of stereo cameras to provide both visual and depth information, guiding the search and validation of loop closures from a multi-modal perspective. We propose to augment submaps that are created by aggregating stereo point clouds, with visual keyframes. Point clouds matches are found by comparing CSHOT descriptors and validated by clustering while visual matches are established by comparing keyframes using Bag-of-Words (BoW) and ORB descriptors. The relative transformations resulting from both keyframe and point cloud matches are then fused to provide pose constraints between submaps in our graph-based SLAM framework. Using the LRU rover, we performed several tests in both an indoor laboratory environment as well as a challenging planetary analog environment on Mount Etna, Italy. These environments consist of areas where either keyframes or point clouds alone fail to provide adequate matches, thus demonstrating the benefit of the proposed multi-modal approach.

Gaussian Process Gradient Maps for Loop-Closure Detection in Unstructured Planetary Environments

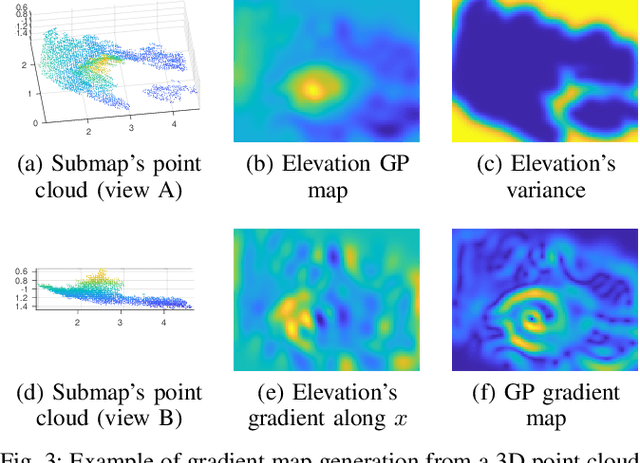
The ability to recognize previously mapped locations is an essential feature for autonomous systems. Unstructured planetary-like environments pose a major challenge to these systems due to the similarity of the terrain. As a result, the ambiguity of the visual appearance makes state-of-the-art visual place recognition approaches less effective than in urban or man-made environments. This paper presents a method to solve the loop closure problem using only spatial information. The key idea is to use a novel continuous and probabilistic representations of terrain elevation maps. Given 3D point clouds of the environment, the proposed approach exploits Gaussian Process (GP) regression with linear operators to generate continuous gradient maps of the terrain elevation information. Traditional image registration techniques are then used to search for potential matches. Loop closures are verified by leveraging both the spatial characteristic of the elevation maps (SE(2) registration) and the probabilistic nature of the GP representation. A submap-based localization and mapping framework is used to demonstrate the validity of the proposed approach. The performance of this pipeline is evaluated and benchmarked using real data from a rover that is equipped with a stereo camera and navigates in challenging, unstructured planetary-like environments in Morocco and on Mt. Etna.