Inferring Lexicographically-Ordered Rewards from Preferences

Modeling the preferences of agents over a set of alternatives is a principal concern in many areas. The dominant approach has been to find a single reward/utility function with the property that alternatives yielding higher rewards are preferred over alternatives yielding lower rewards. However, in many settings, preferences are based on multiple, often competing, objectives; a single reward function is not adequate to represent such preferences. This paper proposes a method for inferring multi-objective reward-based representations of an agent's observed preferences. We model the agent's priorities over different objectives as entering lexicographically, so that objectives with lower priorities matter only when the agent is indifferent with respect to objectives with higher priorities. We offer two example applications in healthcare, one inspired by cancer treatment, the other inspired by organ transplantation, to illustrate how the lexicographically-ordered rewards we learn can provide a better understanding of a decision-maker's preferences and help improve policies when used in reinforcement learning.

Integrating Expert ODEs into Neural ODEs: Pharmacology and Disease Progression

Modeling a system's temporal behaviour in reaction to external stimuli is a fundamental problem in many areas. Pure Machine Learning (ML) approaches often fail in the small sample regime and cannot provide actionable insights beyond predictions. A promising modification has been to incorporate expert domain knowledge into ML models. The application we consider is predicting the progression of disease under medications, where a plethora of domain knowledge is available from pharmacology. Pharmacological models describe the dynamics of carefully-chosen medically meaningful variables in terms of systems of Ordinary Differential Equations (ODEs). However, these models only describe a limited collection of variables, and these variables are often not observable in clinical environments. To close this gap, we propose the latent hybridisation model (LHM) that integrates a system of expert-designed ODEs with machine-learned Neural ODEs to fully describe the dynamics of the system and to link the expert and latent variables to observable quantities. We evaluated LHM on synthetic data as well as real-world intensive care data of COVID-19 patients. LHM consistently outperforms previous works, especially when few training samples are available such as at the beginning of the pandemic.

Piecewise Approximations of Black Box Models for Model Interpretation

Machine Learning models have proved extremely successful for a wide variety of supervised learning problems, but the predictions of many of these models are difficult to interpret. A recent literature interprets the predictions of more general "black-box" machine learning models by approximating these models in terms of simpler models such as piecewise linear or piecewise constant models. Existing literature constructs these approximations in an ad-hoc manner. We provide a tractable dynamic programming algorithm that partitions the feature space into clusters in a principled way and then uses this partition to provide both piecewise constant and piecewise linear interpretations of an arbitrary "black-box" model. When loss is measured in terms of mean squared error, our approximation is optimal (under certain conditions); for more general loss functions, our interpretation is probably approximately optimal (in the sense of PAC learning). Experiments with real and synthetic data show that it continues to provide significant improvements (in terms of mean squared error) over competing approaches.

Constructing Effective Personalized Policies Using Counterfactual Inference from Biased Data Sets with Many Features

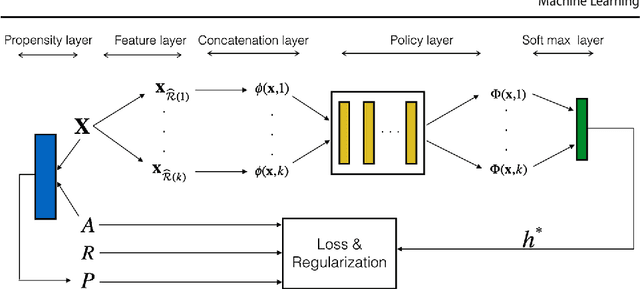
This paper proposes a novel approach for constructing effective personalized policies when the observed data lacks counter-factual information, is biased and possesses many features. The approach is applicable in a wide variety of settings from healthcare to advertising to education to finance. These settings have in common that the decision maker can observe, for each previous instance, an array of features of the instance, the action taken in that instance, and the reward realized -- but not the rewards of actions that were not taken: the counterfactual information. Learning in such settings is made even more difficult because the observed data is typically biased by the existing policy (that generated the data) and because the array of features that might affect the reward in a particular instance -- and hence should be taken into account in deciding on an action in each particular instance -- is often vast. The approach presented here estimates propensity scores for the observed data, infers counterfactuals, identifies a (relatively small) number of features that are (most) relevant for each possible action and instance, and prescribes a policy to be followed. Comparison of the proposed algorithm against the state-of-art algorithm on actual datasets demonstrates that the proposed algorithm achieves a significant improvement in performance.

Learning Optimal Policies from Observational Data

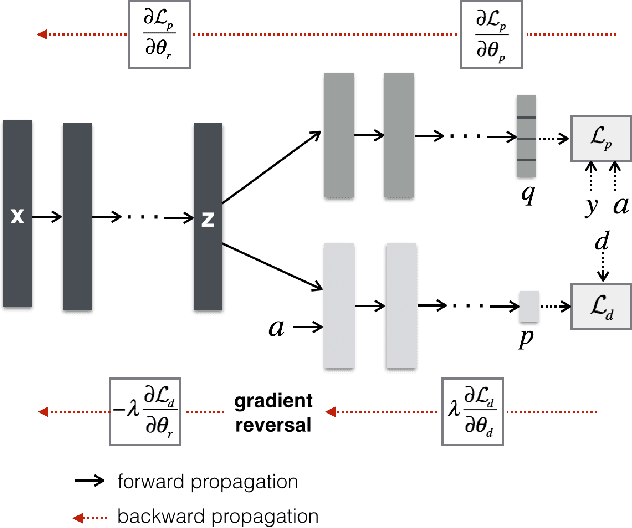
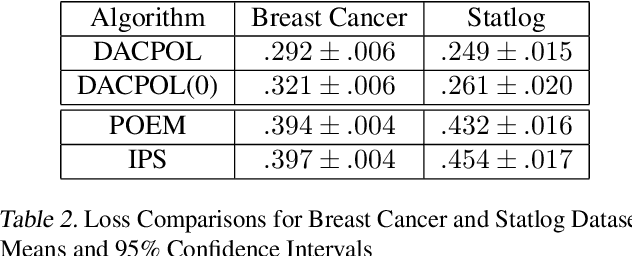
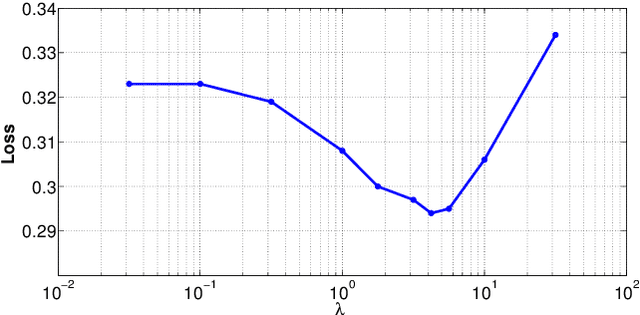
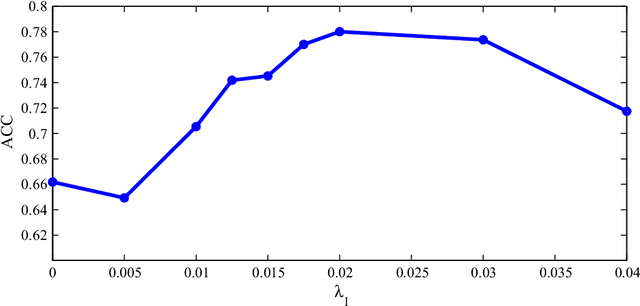
Choosing optimal (or at least better) policies is an important problem in domains from medicine to education to finance and many others. One approach to this problem is through controlled experiments/trials - but controlled experiments are expensive. Hence it is important to choose the best policies on the basis of observational data. This presents two difficult challenges: (i) missing counterfactuals, and (ii) selection bias. This paper presents theoretical bounds on estimation errors of counterfactuals from observational data by making connections to domain adaptation theory. It also presents a principled way of choosing optimal policies using domain adversarial neural networks. We illustrate the effectiveness of domain adversarial training together with various features of our algorithm on a semi-synthetic breast cancer dataset and a supervised UCI dataset (Statlog).

ToPs: Ensemble Learning with Trees of Predictors

We present a new approach to ensemble learning. Our approach constructs a tree of subsets of the feature space and associates a predictor (predictive model) - determined by training one of a given family of base learners on an endogenously determined training set - to each node of the tree; we call the resulting object a tree of predictors. The (locally) optimal tree of predictors is derived recursively; each step involves jointly optimizing the split of the terminal nodes of the previous tree and the choice of learner and training set (hence predictor) for each set in the split. The feature vector of a new instance determines a unique path through the optimal tree of predictors; the final prediction aggregates the predictions of the predictors along this path. We derive loss bounds for the final predictor in terms of the Rademacher complexity of the base learners. We report the results of a number of experiments on a variety of datasets, showing that our approach provides statistically significant improvements over state-of-the-art machine learning algorithms, including various ensemble learning methods. Our approach works because it allows us to endogenously create more complex learners - when needed - and endogenously match both the learner and the training set to the characteristics of the dataset while still avoiding over-fitting.

Estimating Missing Data in Temporal Data Streams Using Multi-directional Recurrent Neural Networks

Missing data is a ubiquitous problem. It is especially challenging in medical settings because many streams of measurements are collected at different - and often irregular - times. Accurate estimation of those missing measurements is critical for many reasons, including diagnosis, prognosis and treatment. Existing methods address this estimation problem by interpolating within data streams or imputing across data streams (both of which ignore important information) or ignoring the temporal aspect of the data and imposing strong assumptions about the nature of the data-generating process and/or the pattern of missing data (both of which are especially problematic for medical data). We propose a new approach, based on a novel deep learning architecture that we call a Multi-directional Recurrent Neural Network (M-RNN) that interpolates within data streams and imputes across data streams. We demonstrate the power of our approach by applying it to five real-world medical datasets. We show that it provides dramatically improved estimation of missing measurements in comparison to 11 state-of-the-art benchmarks (including Spline and Cubic Interpolations, MICE, MissForest, matrix completion and several RNN methods); typical improvements in Root Mean Square Error are between 35% - 50%. Additional experiments based on the same five datasets demonstrate that the improvements provided by our method are extremely robust.