Exact gradients for linear optics with single photons

Though parameter shift rules have drastically improved gradient estimation methods for several types of quantum circuits, leading to improved performance in downstream tasks, so far they have not been transferable to linear optics with single photons. In this work, we derive an analytical formula for the gradients in these circuits with respect to phaseshifters via a generalized parameter shift rule, where the number of parameter shifts depends linearly on the total number of photons. Experimentally, this enables access to derivatives in photonic systems without the need for finite difference approximations. Building on this, we propose two strategies through which one can reduce the number of shifts in the expression, and hence reduce the overall sample complexity. Numerically, we show that this generalized parameter-shift rule can converge to the minimum of a cost function with fewer parameter update steps than alternative techniques. We anticipate that this method will open up new avenues to solving optimization problems with photonic systems, as well as provide new techniques for the experimental characterization and control of linear optical systems.

Learning Group Structure and Disentangled Representations of Dynamical Environments

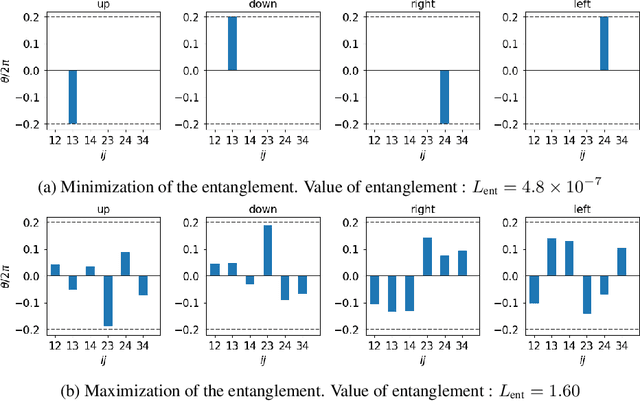
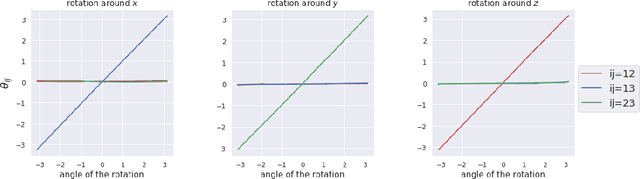
Discovering the underlying structure of a dynamical environment involves learning representations that are interpretable and disentangled, which is a challenging task. In physics, interpretable representations of our universe and its underlying dynamics are formulated in terms of representations of groups of symmetry transformations. We propose a physics-inspired method, built upon the theory of group representation, that learns a representation of an environment structured around the transformations that generate its evolution. Experimentally, we learn the structure of explicitly symmetric environments without supervision while ensuring the interpretability of the representations. We show that the learned representations allow for accurate long-horizon predictions and further demonstrate a correlation between the quality of predictions and disentanglement in the latent space.

Robust Domain Randomization for Reinforcement Learning

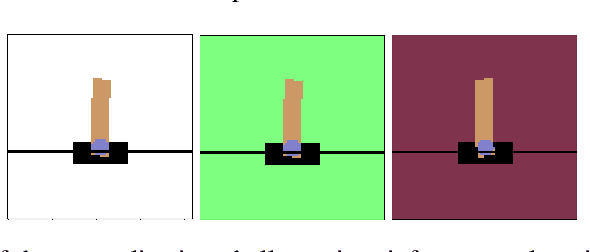
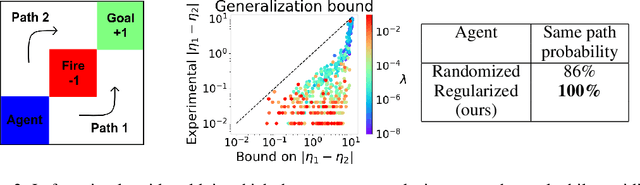
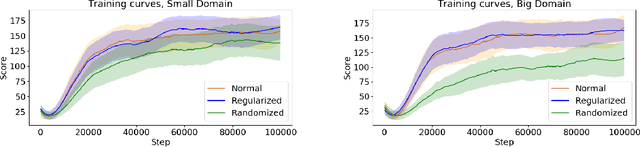
Producing agents that can generalize to a wide range of environments is a significant challenge in reinforcement learning. One method for overcoming this issue is domain randomization, whereby at the start of each training episode some parameters of the environment are randomized so that the agent is exposed to many possible variations. However, domain randomization is highly inefficient and may lead to policies with high variance across domains. In this work, we formalize the domain randomization problem, and show that minimizing the policy's Lipschitz constant with respect to the randomization parameters leads to low variance in the learned policies. We propose a method where the agent only needs to be trained on one variation of the environment, and its learned state representations are regularized during training to minimize this constant. We conduct experiments that demonstrate that our technique leads to more efficient and robust learning than standard domain randomization, while achieving equal generalization scores.

Exploratory Combinatorial Optimization with Reinforcement Learning

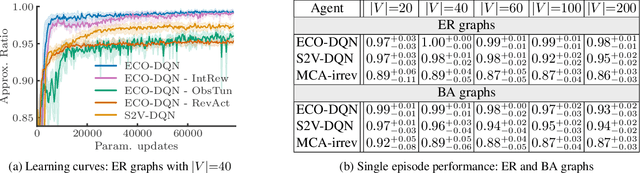
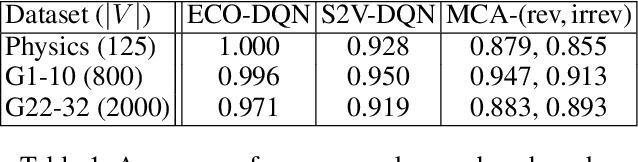
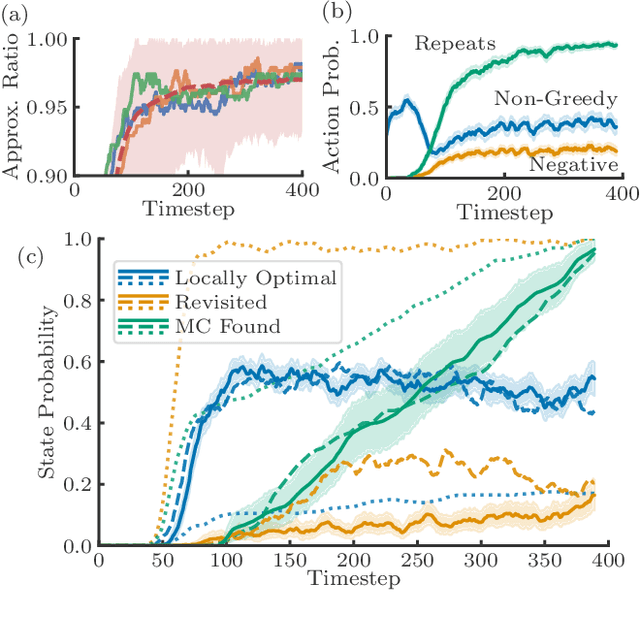
Many real-world problems can be reduced to combinatorial optimization on a graph, where the subset or ordering of vertices that maximize some objective function must be found. With such tasks often NP-hard and analytically intractable, reinforcement learning (RL) has shown promise as a framework with which efficient heuristic methods to tackle these problems can be learned. Previous works construct the solution subset incrementally, adding one element at a time, however, the irreversible nature of this approach prevents the agent from revising its earlier decisions, which may be necessary given the complexity of the optimization task. We instead propose that the agent should seek to continuously improve the solution by learning to explore at test time. Our approach of exploratory combinatorial optimization (ECO-DQN) is, in principle, applicable to any combinatorial problem that can be defined on a graph. Experimentally, we show our method to produce state-of-the-art RL performance on the Maximum Cut problem. Moreover, because ECO-DQN can start from any arbitrary configuration, it can be combined with other search methods to further improve performance, which we demonstrate using a simple random search.

Estimating Risk and Uncertainty in Deep Reinforcement Learning

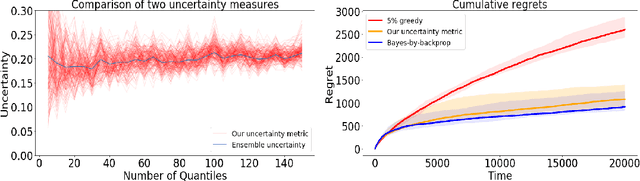
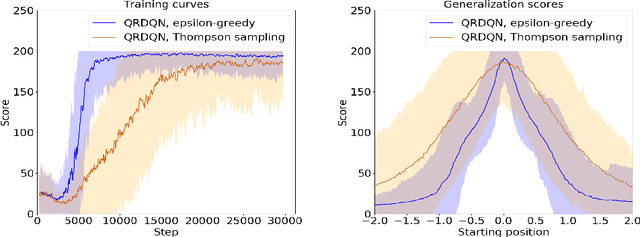
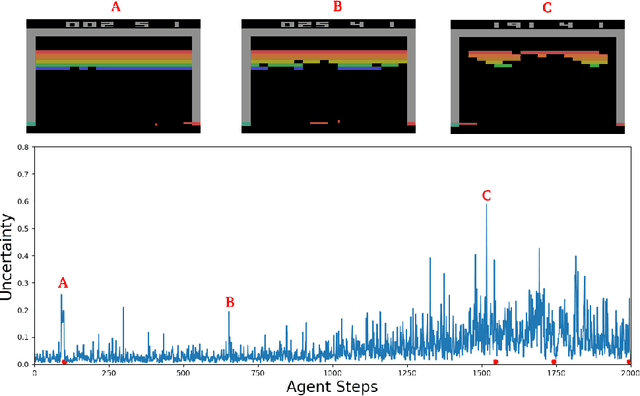
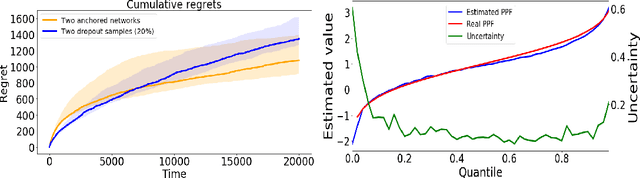
This paper demonstrates a novel method for separately estimating aleatoric risk and epistemic uncertainty in deep reinforcement learning. Aleatoric risk, which arises from inherently stochastic environments or agents, must be accounted for in the design of risk-sensitive algorithms. Epistemic uncertainty, which stems from limited data, is important both for risk-sensitivity and to efficiently explore an environment. We first present a Bayesian framework for learning the return distribution in reinforcement learning, which provides theoretical foundations for quantifying both types of uncertainty. Based on this framework, we show that the disagreement between only two neural networks is sufficient to produce a low-variance estimate of the epistemic uncertainty on the return distribution, thus providing a simple and computationally cheap uncertainty metric. We demonstrate experiments that illustrate our method and some applications.