Deep Reinforcement Learning for Uplink Scheduling in NOMA-URLLC Networks

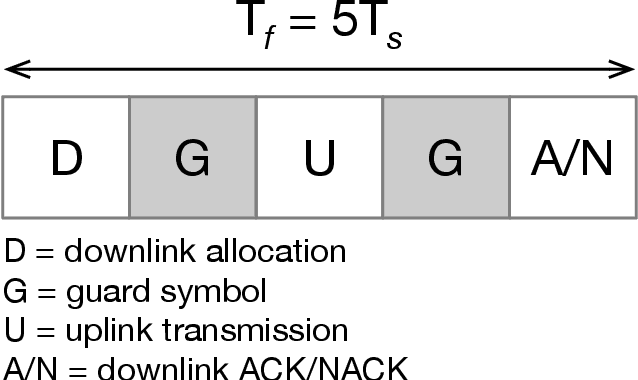
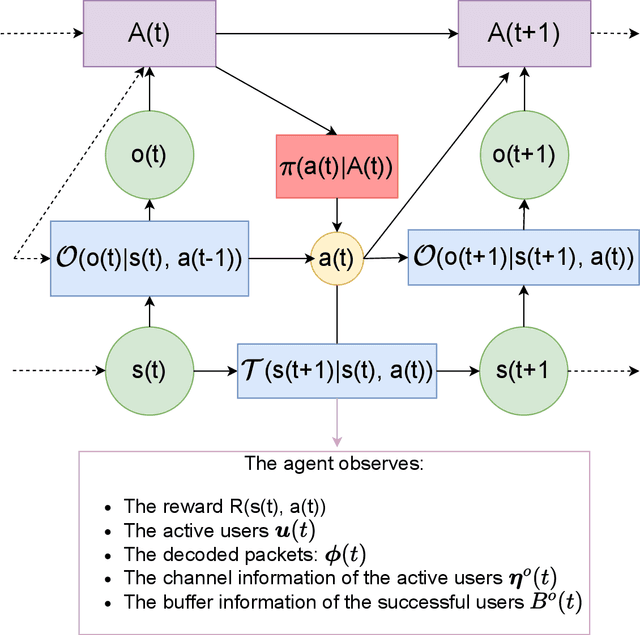
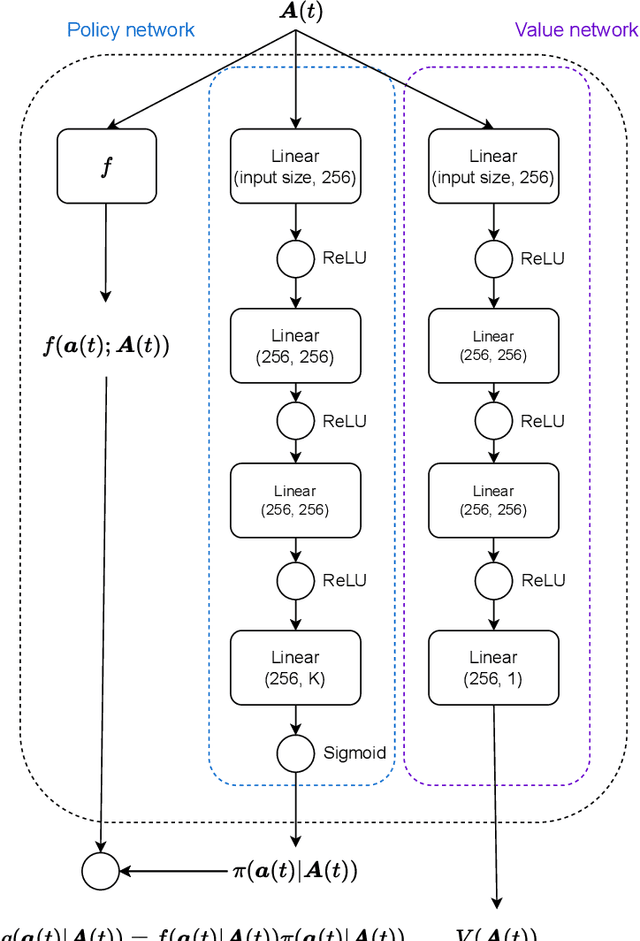
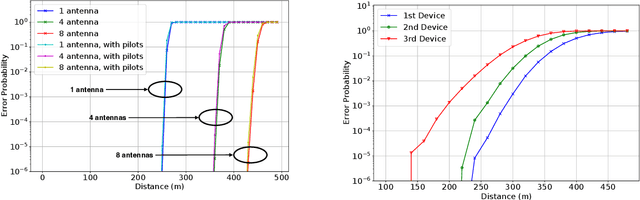
This article addresses the problem of Ultra Reliable Low Latency Communications (URLLC) in wireless networks, a framework with particularly stringent constraints imposed by many Internet of Things (IoT) applications from diverse sectors. We propose a novel Deep Reinforcement Learning (DRL) scheduling algorithm, named NOMA-PPO, to solve the Non-Orthogonal Multiple Access (NOMA) uplink URLLC scheduling problem involving strict deadlines. The challenge of addressing uplink URLLC requirements in NOMA systems is related to the combinatorial complexity of the action space due to the possibility to schedule multiple devices, and to the partial observability constraint that we impose to our algorithm in order to meet the IoT communication constraints and be scalable. Our approach involves 1) formulating the NOMA-URLLC problem as a Partially Observable Markov Decision Process (POMDP) and the introduction of an agent state, serving as a sufficient statistic of past observations and actions, enabling a transformation of the POMDP into a Markov Decision Process (MDP); 2) adapting the Proximal Policy Optimization (PPO) algorithm to handle the combinatorial action space; 3) incorporating prior knowledge into the learning agent with the introduction of a Bayesian policy. Numerical results reveal that not only does our approach outperform traditional multiple access protocols and DRL benchmarks on 3GPP scenarios, but also proves to be robust under various channel and traffic configurations, efficiently exploiting inherent time correlations.

Estimating Risk and Uncertainty in Deep Reinforcement Learning

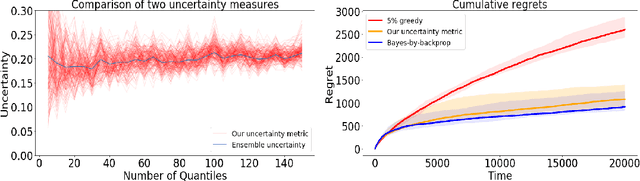
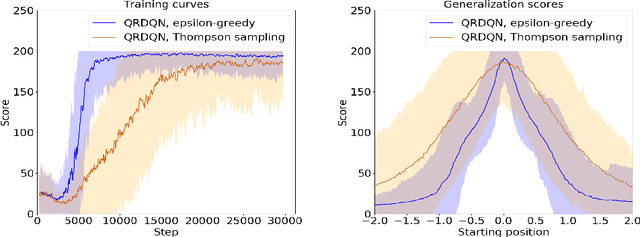
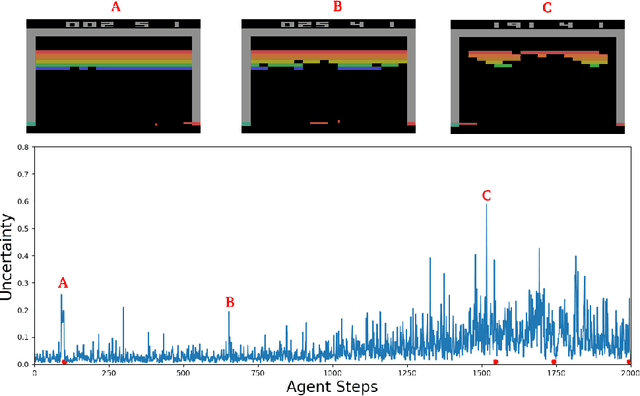
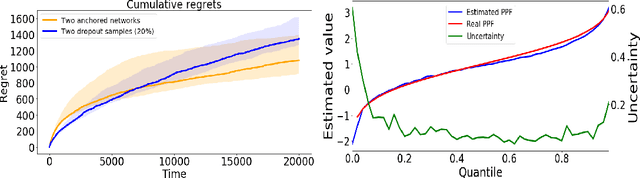
This paper demonstrates a novel method for separately estimating aleatoric risk and epistemic uncertainty in deep reinforcement learning. Aleatoric risk, which arises from inherently stochastic environments or agents, must be accounted for in the design of risk-sensitive algorithms. Epistemic uncertainty, which stems from limited data, is important both for risk-sensitivity and to efficiently explore an environment. We first present a Bayesian framework for learning the return distribution in reinforcement learning, which provides theoretical foundations for quantifying both types of uncertainty. Based on this framework, we show that the disagreement between only two neural networks is sufficient to produce a low-variance estimate of the epistemic uncertainty on the return distribution, thus providing a simple and computationally cheap uncertainty metric. We demonstrate experiments that illustrate our method and some applications.