Robust Domain Randomization for Reinforcement Learning

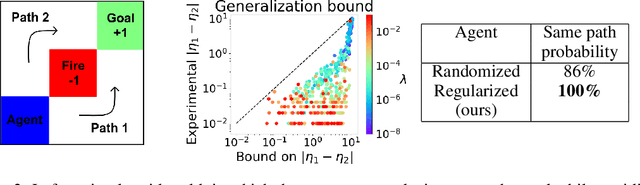
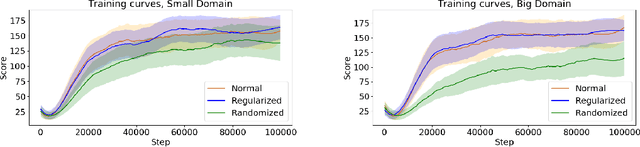
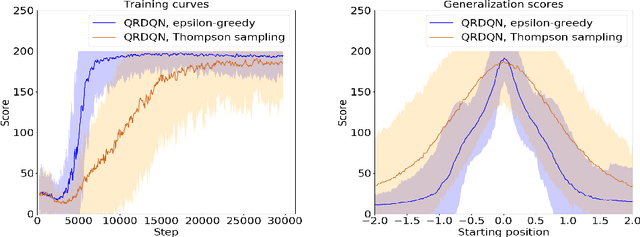
Producing agents that can generalize to a wide range of environments is a significant challenge in reinforcement learning. One method for overcoming this issue is domain randomization, whereby at the start of each training episode some parameters of the environment are randomized so that the agent is exposed to many possible variations. However, domain randomization is highly inefficient and may lead to policies with high variance across domains. In this work, we formalize the domain randomization problem, and show that minimizing the policy's Lipschitz constant with respect to the randomization parameters leads to low variance in the learned policies. We propose a method where the agent only needs to be trained on one variation of the environment, and its learned state representations are regularized during training to minimize this constant. We conduct experiments that demonstrate that our technique leads to more efficient and robust learning than standard domain randomization, while achieving equal generalization scores.

Estimating Risk and Uncertainty in Deep Reinforcement Learning

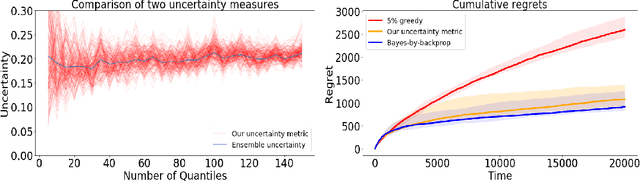
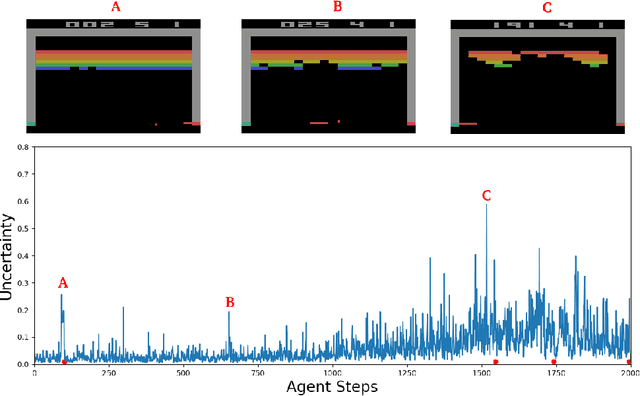
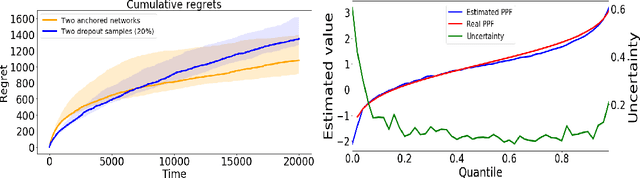
This paper demonstrates a novel method for separately estimating aleatoric risk and epistemic uncertainty in deep reinforcement learning. Aleatoric risk, which arises from inherently stochastic environments or agents, must be accounted for in the design of risk-sensitive algorithms. Epistemic uncertainty, which stems from limited data, is important both for risk-sensitivity and to efficiently explore an environment. We first present a Bayesian framework for learning the return distribution in reinforcement learning, which provides theoretical foundations for quantifying both types of uncertainty. Based on this framework, we show that the disagreement between only two neural networks is sufficient to produce a low-variance estimate of the epistemic uncertainty on the return distribution, thus providing a simple and computationally cheap uncertainty metric. We demonstrate experiments that illustrate our method and some applications.