Learning Group Structure and Disentangled Representations of Dynamical Environments
Paper and Code
Feb 17, 2020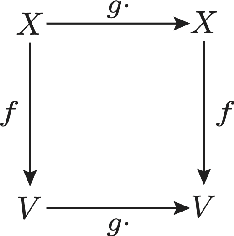

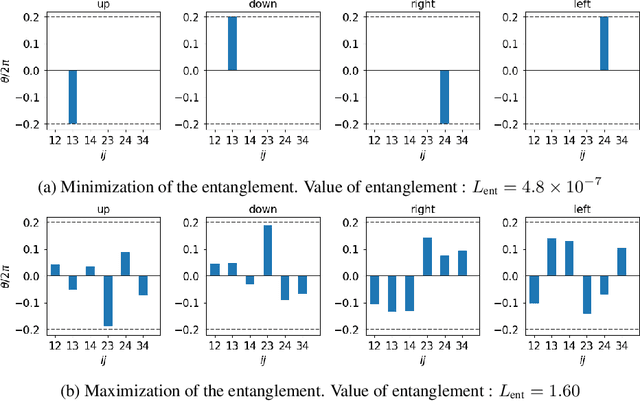
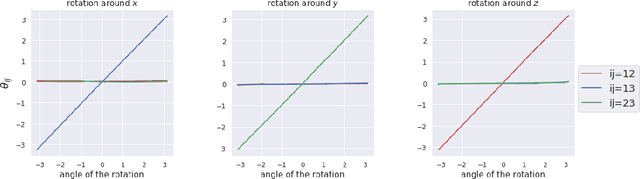
Discovering the underlying structure of a dynamical environment involves learning representations that are interpretable and disentangled, which is a challenging task. In physics, interpretable representations of our universe and its underlying dynamics are formulated in terms of representations of groups of symmetry transformations. We propose a physics-inspired method, built upon the theory of group representation, that learns a representation of an environment structured around the transformations that generate its evolution. Experimentally, we learn the structure of explicitly symmetric environments without supervision while ensuring the interpretability of the representations. We show that the learned representations allow for accurate long-horizon predictions and further demonstrate a correlation between the quality of predictions and disentanglement in the latent space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge