GMP-AR: Granularity Message Passing and Adaptive Reconciliation for Temporal Hierarchy Forecasting

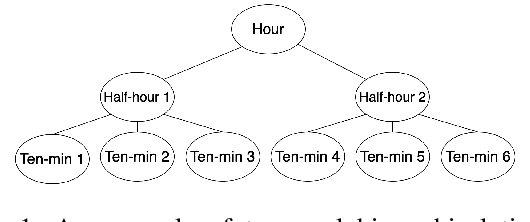
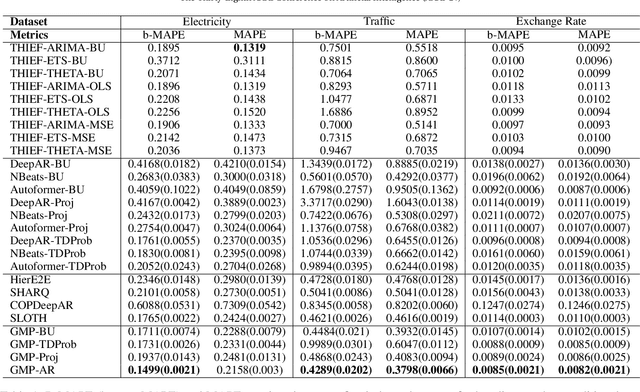
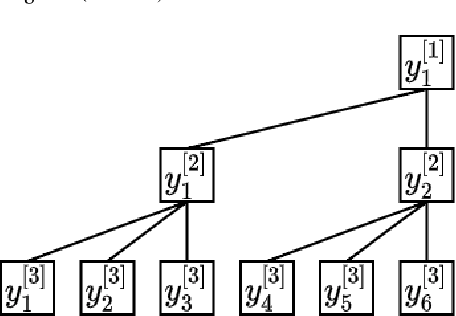
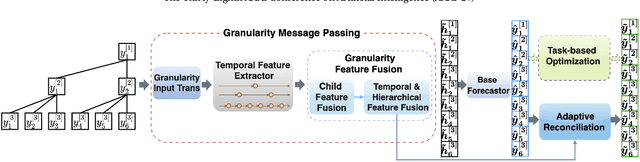
Time series forecasts of different temporal granularity are widely used in real-world applications, e.g., sales prediction in days and weeks for making different inventory plans. However, these tasks are usually solved separately without ensuring coherence, which is crucial for aligning downstream decisions. Previous works mainly focus on ensuring coherence with some straightforward methods, e.g., aggregation from the forecasts of fine granularity to the coarse ones, and allocation from the coarse granularity to the fine ones. These methods merely take the temporal hierarchical structure to maintain coherence without improving the forecasting accuracy. In this paper, we propose a novel granularity message-passing mechanism (GMP) that leverages temporal hierarchy information to improve forecasting performance and also utilizes an adaptive reconciliation (AR) strategy to maintain coherence without performance loss. Furthermore, we introduce an optimization module to achieve task-based targets while adhering to more real-world constraints. Experiments on real-world datasets demonstrate that our framework (GMP-AR) achieves superior performances on temporal hierarchical forecasting tasks compared to state-of-the-art methods. In addition, our framework has been successfully applied to a real-world task of payment traffic management in Alipay by integrating with the task-based optimization module.

Deep Optimal Timing Strategies for Time Series

Deciding the best future execution time is a critical task in many business activities while evolving time series forecasting, and optimal timing strategy provides such a solution, which is driven by observed data. This solution has plenty of valuable applications to reduce the operation costs. In this paper, we propose a mechanism that combines a probabilistic time series forecasting task and an optimal timing decision task as a first systematic attempt to tackle these practical problems with both solid theoretical foundation and real-world flexibility. Specifically, it generates the future paths of the underlying time series via probabilistic forecasting algorithms, which does not need a sophisticated mathematical dynamic model relying on strong prior knowledge as most other common practices. In order to find the optimal execution time, we formulate the decision task as an optimal stopping problem, and employ a recurrent neural network structure (RNN) to approximate the optimal times. Github repository: \url{github.com/ChenPopper/optimal_timing_TSF}.