Learning Diffusion Model from Noisy Measurement using Principled Expectation-Maximization Method

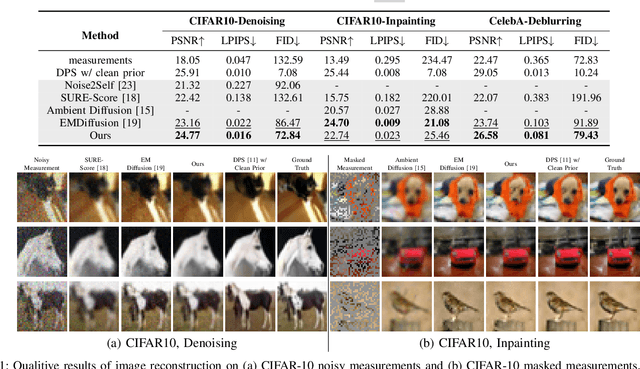
Diffusion models have demonstrated exceptional ability in modeling complex image distributions, making them versatile plug-and-play priors for solving imaging inverse problems. However, their reliance on large-scale clean datasets for training limits their applicability in scenarios where acquiring clean data is costly or impractical. Recent approaches have attempted to learn diffusion models directly from corrupted measurements, but these methods either lack theoretical convergence guarantees or are restricted to specific types of data corruption. In this paper, we propose a principled expectation-maximization (EM) framework that iteratively learns diffusion models from noisy data with arbitrary corruption types. Our framework employs a plug-and-play Monte Carlo method to accurately estimate clean images from noisy measurements, followed by training the diffusion model using the reconstructed images. This process alternates between estimation and training until convergence. We evaluate the performance of our method across various imaging tasks, including inpainting, denoising, and deblurring. Experimental results demonstrate that our approach enables the learning of high-fidelity diffusion priors from noisy data, significantly enhancing reconstruction quality in imaging inverse problems.

Integrating Amortized Inference with Diffusion Models for Learning Clean Distribution from Corrupted Images

Diffusion models (DMs) have emerged as powerful generative models for solving inverse problems, offering a good approximation of prior distributions of real-world image data. Typically, diffusion models rely on large-scale clean signals to accurately learn the score functions of ground truth clean image distributions. However, such a requirement for large amounts of clean data is often impractical in real-world applications, especially in fields where data samples are expensive to obtain. To address this limitation, in this work, we introduce \emph{FlowDiff}, a novel joint training paradigm that leverages a conditional normalizing flow model to facilitate the training of diffusion models on corrupted data sources. The conditional normalizing flow try to learn to recover clean images through a novel amortized inference mechanism, and can thus effectively facilitate the diffusion model's training with corrupted data. On the other side, diffusion models provide strong priors which in turn improve the quality of image recovery. The flow model and the diffusion model can therefore promote each other and demonstrate strong empirical performances. Our elaborate experiment shows that FlowDiff can effectively learn clean distributions across a wide range of corrupted data sources, such as noisy and blurry images. It consistently outperforms existing baselines with significant margins under identical conditions. Additionally, we also study the learned diffusion prior, observing its superior performance in downstream computational imaging tasks, including inpainting, denoising, and deblurring.

An Expectation-Maximization Algorithm for Training Clean Diffusion Models from Corrupted Observations

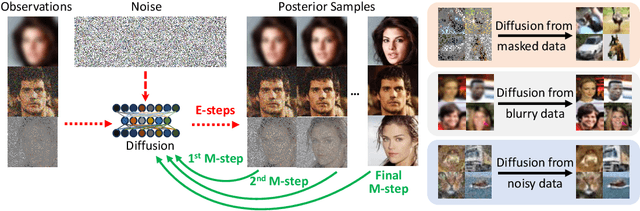
Diffusion models excel in solving imaging inverse problems due to their ability to model complex image priors. However, their reliance on large, clean datasets for training limits their practical use where clean data is scarce. In this paper, we propose EMDiffusion, an expectation-maximization (EM) approach to train diffusion models from corrupted observations. Our method alternates between reconstructing clean images from corrupted data using a known diffusion model (E-step) and refining diffusion model weights based on these reconstructions (M-step). This iterative process leads the learned diffusion model to gradually converge to the true clean data distribution. We validate our method through extensive experiments on diverse computational imaging tasks, including random inpainting, denoising, and deblurring, achieving new state-of-the-art performance.

Blind Inversion using Latent Diffusion Priors

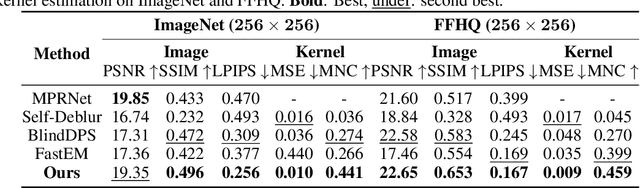
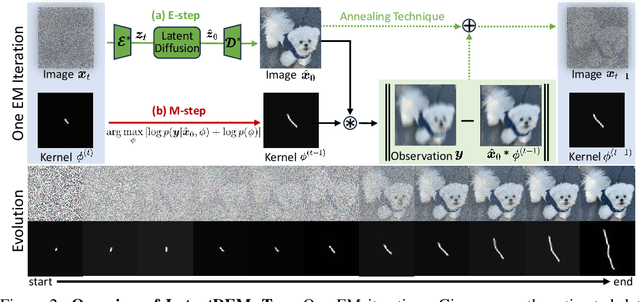
Diffusion models have emerged as powerful tools for solving inverse problems due to their exceptional ability to model complex prior distributions. However, existing methods predominantly assume known forward operators (i.e., non-blind), limiting their applicability in practical settings where acquiring such operators is costly. Additionally, many current approaches rely on pixel-space diffusion models, leaving the potential of more powerful latent diffusion models (LDMs) underexplored. In this paper, we introduce LatentDEM, an innovative technique that addresses more challenging blind inverse problems using latent diffusion priors. At the core of our method is solving blind inverse problems within an iterative Expectation-Maximization (EM) framework: (1) the E-step recovers clean images from corrupted observations using LDM priors and a known forward model, and (2) the M-step estimates the forward operator based on the recovered images. Additionally, we propose two novel optimization techniques tailored for LDM priors and EM frameworks, yielding more accurate and efficient blind inversion results. As a general framework, LatentDEM supports both linear and non-linear inverse problems. Beyond common 2D image restoration tasks, it enables new capabilities in non-linear 3D inverse rendering problems. We validate LatentDEM's performance on representative 2D blind deblurring and 3D sparse-view reconstruction tasks, demonstrating its superior efficacy over prior arts.